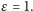Stożkowe
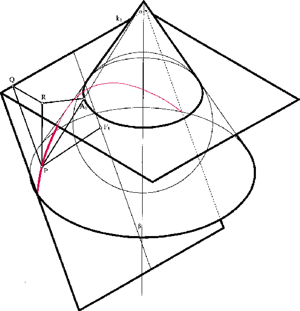
Przecięcie stożka płaszczyzną
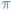 nieprzechodzącą przez wierzchołek to
stożkowa...
nieprzechodzącą przez wierzchołek to
stożkowa...

Jeśli oś stożka tworzy z płaszczyzną
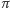 kąt (nazwijmy go
kąt (nazwijmy go
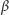 )
większy niż z tworzącą
)
większy niż z tworzącą
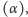 to stożkowa jest elipsą, gdy równy –
parabolą, gdy mniejszy – hiperbolą. Wpisując w stożek sfery styczne do
płaszczyzny
to stożkowa jest elipsą, gdy równy –
parabolą, gdy mniejszy – hiperbolą. Wpisując w stożek sfery styczne do
płaszczyzny
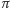 (dla paraboli jest tylko jedna taka sfera), otrzymujemy jako
punkty styczności ogniska stożkowej, a jako przecięcia płaszczyzn zawierających
okręgi, wzdłuż których sfery są styczne do stożka, z płaszczyzną
(dla paraboli jest tylko jedna taka sfera), otrzymujemy jako
punkty styczności ogniska stożkowej, a jako przecięcia płaszczyzn zawierających
okręgi, wzdłuż których sfery są styczne do stożka, z płaszczyzną
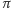 –
kierownice stożkowej.
–
kierownice stożkowej.
Ponieważ wszystkie odcinki stycznych do sfery z tego samego punktu są
równe, więc
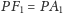 i (dla hiperboli i elipsy)
i (dla hiperboli i elipsy)
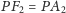 oraz
oraz
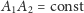 (bo jest to odcinek tworzącej stożka między dwiema
płaszczyznami prostopadłymi do jego osi). Zatem dla hiperboli
(bo jest to odcinek tworzącej stożka między dwiema
płaszczyznami prostopadłymi do jego osi). Zatem dla hiperboli
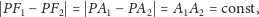 |
czyli moduł różnicy odległości dowolnego punktu od ognisk jest stały; dla elipsy
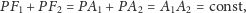 |
czyli suma odległości dowolnego punktu od ognisk jest stała. Jeśli
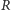 jest
rzutem
jest
rzutem
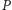 na płaszczyznę okręgu styczności i
na płaszczyznę okręgu styczności i
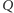 jest rzutem
jest rzutem
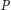 na (bliższą) kierownicę
na (bliższą) kierownicę
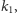 to
to
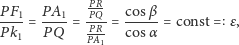 |
czyli stosunek odległości dowolnego punktu stożkowej od ogniska i od
kierownicy jest stały. Zatem mamy dla hiperboli
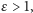 dla elipsy
dla elipsy
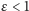 i dla paraboli
i dla paraboli