Kącik przestrzenny
Płaszczyzny przecinające się w punkcie
W tym kąciku przyjrzymy się metodom rozwiązywania zadań o przecinaniu się płaszczyzn. Jedną z nich jest wskazanie punktu przecięcia i udowodnienie, że należy do każdej z rozważanych płaszczyzn.
Jednym z klasycznych chwytów dowodzenia współpękowości trzech prostych na płaszczyźnie jest twierdzenie Cevy. Okazuje się, że ma ono swój odpowiednik w przestrzeni.
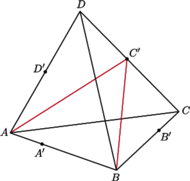
Rys. 1
Twierdzenie (Twierdzenie Cevy). Dany jest czworościan
 i punkty
i punkty
 leżące odpowiednio wewnątrz krawędzi
leżące odpowiednio wewnątrz krawędzi
 (Rys. 1). Wówczas płaszczyzny
(Rys. 1). Wówczas płaszczyzny
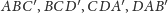 przecinają się
w jednym punkcie wtedy i tylko wtedy, gdy
przecinają się
w jednym punkcie wtedy i tylko wtedy, gdy
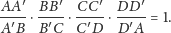 |
Rys. 2
Dowód. Załóżmy najpierw, że dane płaszczyzny mają punkt wspólny
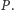 Ponieważ prosta
Ponieważ prosta
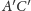 jest częścią wspólną płaszczyzn
jest częścią wspólną płaszczyzn
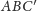 i
i
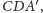 zaś prosta
zaś prosta
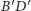 jest częścią wspólną
płaszczyzn
jest częścią wspólną
płaszczyzn
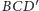 i
i
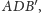 więc punkt
więc punkt
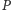 należy do obu
tych prostych (Rys. 2). To dowodzi, że punkty
należy do obu
tych prostych (Rys. 2). To dowodzi, że punkty
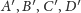 leżą na
jednej płaszczyźnie
leżą na
jednej płaszczyźnie
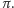
Rys. 3
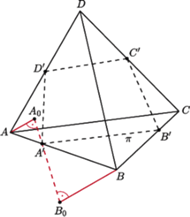
Rys. 4
Niech
 będą rzutami prostokątnymi punktów
będą rzutami prostokątnymi punktów
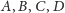 na płaszczyznę
na płaszczyznę
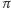 (Rys. 3). Punkty
(Rys. 3). Punkty
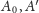 i
i
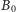 są
współliniowe, co na mocy twierdzenia Talesa prowadzi do równości
są
współliniowe, co na mocy twierdzenia Talesa prowadzi do równości
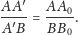 |
Analogicznie dowodzimy, że
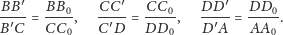 |
Mnożąc otrzymane stosunki, dostajemy tezę.
Przyjmijmy teraz, że
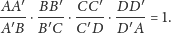 |
Niech
 będzie punktem wspólnym odcinków
będzie punktem wspólnym odcinków
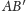 i
i
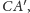 zaś
zaś
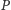 punktem przecięcia płaszczyzny
punktem przecięcia płaszczyzny
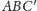 z odcinkiem
z odcinkiem
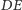 (Rys. 4).
Punkt
(Rys. 4).
Punkt
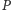 należy do płaszczyzn
należy do płaszczyzn
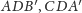 i
i
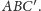 Niech
Niech
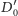 będzie punktem przecięcia płaszczyzny
będzie punktem przecięcia płaszczyzny
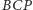 z krawędzią
z krawędzią
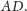 Wtedy na mocy wcześniej udowodnionej części twierdzenia
dostajemy
Wtedy na mocy wcześniej udowodnionej części twierdzenia
dostajemy
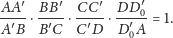 |
W takim razie
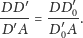 |
Stąd wniosek, że
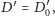 co kończy dowód twierdzenia.
co kończy dowód twierdzenia.
Na koniec podajemy kilka zadań dla Czytelników.