Siatka czworościanu
Czworościan to ostrosłup. Wybieramy jedną ścianę – „podstawę”; trzy ściany „boczne” odchylamy na zewnątrz, jakby były na zawiasach. Gdy się ułożą w płaszczyźnie podstawy, uzyskamy układ czterech trójkątów – płaską siatkę czworościanu; może ona ułatwić (lub utrudnić) jego wizualizację...

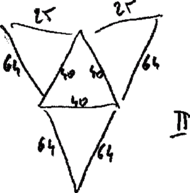

W zawodach okręgowych LXIV Olimpiady Matematycznej pojawiło się zadanie:
Zadanie. Czy istnieje para czworościanów, których ściany można
ponumerować odpowiednio
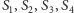 oraz
oraz
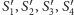 tak, by dla
tak, by dla
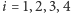 ściana
ściana
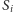 była
trójkątem podobnym do
była
trójkątem podobnym do
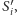 a przy tym te czworościany nie są
bryłami podobnymi?
a przy tym te czworościany nie są
bryłami podobnymi?
Nietrudno zgadnąć, że takie pary istnieją. Uczestnicy zawodów
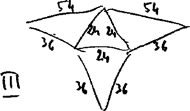
wskazywali różne przykłady. Najczęściej rysowali siatki czworościanów,
podając długości krawędzi. Rysunki – bez zachowania proporcji – należało
traktować wyłącznie jako schematy, jak tu obok. Widzimy jedną parę
siatek, I i II, oraz inną parę, III i IV. W obu tych parach podobieństwa
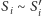 są jasne; przy tym skala podobieństwa pewnych par trójkątów
jest różna od skali innych par, dlatego siatki reprezentują bryły niepodobne.
są jasne; przy tym skala podobieństwa pewnych par trójkątów
jest różna od skali innych par, dlatego siatki reprezentują bryły niepodobne.
Który przykład lepszy? Istotnej różnicy niby nie widać. Gdyby rysunki były staranne, może dostrzeglibyśmy, że różnica jest zasadnicza. Z trójkątów w schematach I i II nie da się w przestrzeni złożyć czworościanów! Z siatek III i IV – da się. Jak to uzasadnić?
Są różne sposoby – na przykład tak: wysokości dwóch
trójkątów równoramiennych, widocznych w siatce III, wynoszą
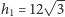 i
i
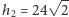 ; deltoid utworzony przez te trójkąty
zaczynamy zginać wzdłuż przekątnej i chcemy, by poruszające się wierzchołki
znalazły się w odległości
; deltoid utworzony przez te trójkąty
zaczynamy zginać wzdłuż przekątnej i chcemy, by poruszające się wierzchołki
znalazły się w odległości
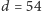 ; do tego potrzeba i wystarcza, by był
spełniony warunek
; do tego potrzeba i wystarcza, by był
spełniony warunek
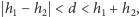 co dla tych wartości
szczęśliwie ma miejsce. Podobnie w układzie IV – ale nie w układach I i II;
one nie są siatkami czworościanów.
co dla tych wartości
szczęśliwie ma miejsce. Podobnie w układzie IV – ale nie w układach I i II;
one nie są siatkami czworościanów.
Obejrzenie licznych przykładów – dobrych i złych – w sposób naturalny rodzi
pytanie: dany trójkąt o bokach
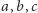 oraz trzy odcinki o długościach
oraz trzy odcinki o długościach
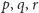 ; znaleźć warunek algebraiczny konieczy i dostateczny,
by istniał czworościan o podstawie
; znaleźć warunek algebraiczny konieczy i dostateczny,
by istniał czworościan o podstawie
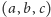 i krawędziach
i krawędziach
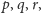 odpowiednio przeciwległych do
odpowiednio przeciwległych do
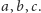 Otóż da się (być
może, nieoczekiwanie) uzyskać ów warunek, rachując na liczbach
zespolonych – w płaszczyźnie podstawy.
Otóż da się (być
może, nieoczekiwanie) uzyskać ów warunek, rachując na liczbach
zespolonych – w płaszczyźnie podstawy.
Nie tracimy ogólności przyjmując, że wierzchołki podstawy są reprezentowane
przez liczby zespolone o module
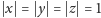 (zysk dobrze znany:
(zysk dobrze znany:
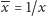 ). Wówczas
). Wówczas
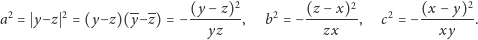 | (1) |
Wprowadźmy oznaczenie
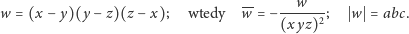 | (2) |
Dalej przydadzą się jeszcze takie zależności (oszczędzimy Czytelnikom szczegółowych rachunków, zachęcając do samodzielnego ich uzupełnienia):
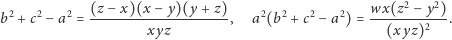 | (3) |
Teraz trochę geometrii. Okręgi
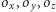 o środkach
o środkach
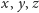 i promieniach
i promieniach
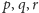 są okręgami wielkimi trzech sfer
w przestrzeni. Nasze pytanie brzmi: czy te sfery mają punkt wspólny? Punkt ów
byłby wierzchołkiem szukanego ostrosłupa. Spodek opuszczonej z niego
wysokości musi leżeć na prostej przechodzącej przez punkty przecięcia
okręgów
są okręgami wielkimi trzech sfer
w przestrzeni. Nasze pytanie brzmi: czy te sfery mają punkt wspólny? Punkt ów
byłby wierzchołkiem szukanego ostrosłupa. Spodek opuszczonej z niego
wysokości musi leżeć na prostej przechodzącej przez punkty przecięcia
okręgów
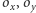 ; również na analogicznej prostej dla okręgów
; również na analogicznej prostej dla okręgów
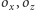 i dla
i dla
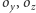 (jeżeli któreś dwa okręgi się nie przecinają, to
sfery na pewno się nie spotkają).
(jeżeli któreś dwa okręgi się nie przecinają, to
sfery na pewno się nie spotkają).
Problem sprowadza się do pytania płaskiego: czy trzy osie potęgowe, utworzone dla trzech par z tej trójki okręgów, przecinają się w punkcie, leżącym wewnątrz nich?
Punkt ów jest reprezentowany przez liczbę zespoloną
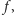 scharakteryzowaną
równościami
scharakteryzowaną
równościami
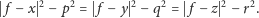 | (4) |
Oznaczmy tę wspólną wartość przez
 ; to potęga punktu
; to potęga punktu
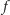 względem każdego z trzech okręgów. Czworościan, o który
chodzi, istnieje wtedy i tylko wtedy, gdy
względem każdego z trzech okręgów. Czworościan, o który
chodzi, istnieje wtedy i tylko wtedy, gdy
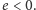
Gdy zapiszemy
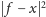 jako
jako
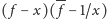 (podobnie
(podobnie
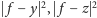 ) i wymnożymy nawiasy, składnik
) i wymnożymy nawiasy, składnik
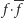 w równaniach
(4) ulegnie redukcji, pozostawiając układ dwóch równań liniowych
z niewiadomymi
w równaniach
(4) ulegnie redukcji, pozostawiając układ dwóch równań liniowych
z niewiadomymi
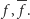
Jego rozwiązanie jest natychmiastowe i daje wynik
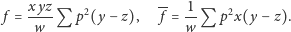 | (5) |
Liczba
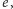 równa każdemu z trzech wyrażeń, występujących w (4),
jest oczywiście także ich średnią arytmetyczną:
równa każdemu z trzech wyrażeń, występujących w (4),
jest oczywiście także ich średnią arytmetyczną:
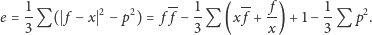 | (6) |
Po wprowadzeniu wzorów (5) i uporządkowaniu wszystkiego według potęg
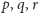 dostaniemy wielomian względem
dostaniemy wielomian względem
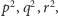 w którym jako
współczynniki pojawią się – po krótkich przekształceniach – wyrażenia,
napisane po prawych stronach równości (3), mnożone lub dzielone przez
pewne potęgi liczby
w którym jako
współczynniki pojawią się – po krótkich przekształceniach – wyrażenia,
napisane po prawych stronach równości (3), mnożone lub dzielone przez
pewne potęgi liczby
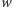 oraz iloczynu
oraz iloczynu
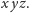 Uwzględniając jeszcze
związki (2), pozbywamy się w ogóle liter
Uwzględniając jeszcze
związki (2), pozbywamy się w ogóle liter
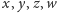 i doprowadzamy do
wyniku
i doprowadzamy do
wyniku
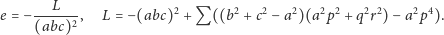 | (7) |
Licznik
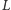 można zapisać w równoważnych postaciach (Czytelniku,
sprawdź!):
można zapisać w równoważnych postaciach (Czytelniku,
sprawdź!):

zaś warunek istnienia czworościanu brzmi:
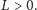
Jego ściany to trójkąty o bokach
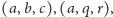
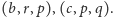 Z postaci wyznacznikowej wzoru (8) widać,
że nic się nie zmieni, gdy inną z tych trójek – np.
Z postaci wyznacznikowej wzoru (8) widać,
że nic się nie zmieni, gdy inną z tych trójek – np.
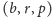 –
przyjmiemy za ścianę podstawy. Dokładniej: po zastąpieniu szóstki
uporządkowanej
–
przyjmiemy za ścianę podstawy. Dokładniej: po zastąpieniu szóstki
uporządkowanej
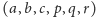 przez
przez
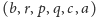 wartość
wartość
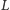 będzie taka sama; w wyznaczniku nastąpi jednoczesna permutacja
wierszy i kolumn.
będzie taka sama; w wyznaczniku nastąpi jednoczesna permutacja
wierszy i kolumn.
Zaczęliśmy od trójkąta o bokach
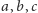 oraz trójki liczb
oraz trójki liczb
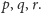 Gdyby mówić, bardziej abstrakcyjnie, o szóstce liczb dodatnich
Gdyby mówić, bardziej abstrakcyjnie, o szóstce liczb dodatnich
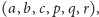 należałoby jeszcze dołączyć warunek trójkąta dla
trójki
należałoby jeszcze dołączyć warunek trójkąta dla
trójki
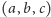 : wówczas jeśli
: wówczas jeśli
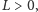 to czworościan
istnieje, więc automatycznie w każdej z trójek
to czworościan
istnieje, więc automatycznie w każdej z trójek
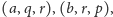
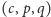 warunek trójkąta jest spełniony. Podsumowując:
warunek trójkąta jest spełniony. Podsumowując:
Dla liczb
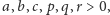 czworościan o ścianach
czworościan o ścianach
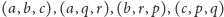 istnieje wtedy i tylko wtedy, gdy
istnieje wtedy i tylko wtedy, gdy
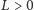 oraz w co najmniej jednej z tych trójek (równoważnie: we
wszystkich) spełniony jest warunek trójkąta.
oraz w co najmniej jednej z tych trójek (równoważnie: we
wszystkich) spełniony jest warunek trójkąta.
Całe rozumowanie można też prowadzić inną metodą. Wymaga ona jednak
wstępnego założenia, że istnieją trzy z czterech wymienionych trójkątów –
na przykład trójkąty
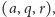
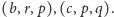 Gdy miary ich
kątów między bokami
Gdy miary ich
kątów między bokami
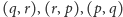 mają sumę mniejszą od
mają sumę mniejszą od
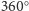 oraz spełniają warunek trójkąta (a to można kontrolować
wzorem kosinusów), wówczas da się zaczepić odcinki
oraz spełniają warunek trójkąta (a to można kontrolować
wzorem kosinusów), wówczas da się zaczepić odcinki
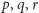 w jednym
punkcie przestrzeni i zbudować żądany czworościan. Rzecz jasna, wychodzi
znów warunek
w jednym
punkcie przestrzeni i zbudować żądany czworościan. Rzecz jasna, wychodzi
znów warunek
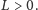
Trygonometryczne wyprowadzenie warunku
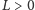 znajduje się w pracy:
K. Wirth, A. S. Dreidling, Edge lengths determining tetrahedrons, Elemente d.
Math. 64 (2009)
znajduje się w pracy:
K. Wirth, A. S. Dreidling, Edge lengths determining tetrahedrons, Elemente d.
Math. 64 (2009)
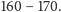
Wróćmy jeszcze do wzoru (4):
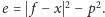 Gdy czworościan
istnieje, twierdzenie Pitagorasa pokazuje, że liczba
Gdy czworościan
istnieje, twierdzenie Pitagorasa pokazuje, że liczba
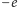 jest kwadratem
wysokości
jest kwadratem
wysokości
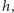 opuszczonej na płaszczyznę ściany
opuszczonej na płaszczyznę ściany
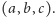 Ale
iloraz we wzorze (7) ma w liczniku i w mianowniku wyrażenia jednakowego
stopnia – coś się nie zgadza? To proste – jednorodność została utracona, gdy
przyjęliśmy, że trójkąt
Ale
iloraz we wzorze (7) ma w liczniku i w mianowniku wyrażenia jednakowego
stopnia – coś się nie zgadza? To proste – jednorodność została utracona, gdy
przyjęliśmy, że trójkąt
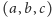 jest wpisany w okrąg o promieniu 1.
Przyjmując, że ten okrąg ma promień
jest wpisany w okrąg o promieniu 1.
Przyjmując, że ten okrąg ma promień
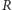 i prowadząc analogiczne
rachunki, doszlibyśmy do równości
i prowadząc analogiczne
rachunki, doszlibyśmy do równości
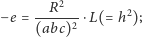 |
wymiar już jest, jak trzeba.
Zważywszy, że pole
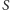 trójkąta
trójkąta
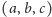 jest dane
wzorem
jest dane
wzorem
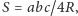 zaś objętość ostrosłupa wzorem
zaś objętość ostrosłupa wzorem
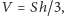 dochodzimy do konkluzji, że wielkość
dochodzimy do konkluzji, że wielkość
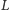 we
wzorach (7), (8) wyraża, z dokładnością do czynnika, kwadrat objętości
rozważanego czworościanu:
we
wzorach (7), (8) wyraża, z dokładnością do czynnika, kwadrat objętości
rozważanego czworościanu:
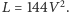 To analogon wzoru Herona dla
pola trójkąta.
To analogon wzoru Herona dla
pola trójkąta.
Na zakończenie słów parę o ocenianiu prac uczestników olimpiady. Przykład „siatki”, która nie jest siatką (nie skleja się w przestrzeni, jak I lub II), był oceniany na zero – trudno inaczej. Przykłady dobrych siatek (jak III i IV, jedynie bez uzasadnienia, że się dadzą skleić) otrzymywały ocenę niezerową – znów: trudno inaczej. Ta niezerowa ocena była jednak daleka od maksymalnej, co wywołało pretensje wielu zawodników: przecież część koncepcyjna została wykonana, zabrakło prostego sprawdzenia. No tak; ale zawodnicy, którzy dali przykłady nieistniejących brył, także wykonali ową pracę koncepcyjną, im też zabrakło jedynie prostego sprawdzenia – tyle, że niewykonalnego. Wszelako autorzy i tych, i tych prac, byli w większości zupełnie nieświadomi problemu realizacji przestrzennej, i jedynie kwestią szczęścia/pecha było znalezienie siatek jak (III, IV)/(I, II). Te prace należało w zasadzie ocenić jednakowo. Na zero? nonsens; na ocenę dodatnią? nonsens. Dedykujemy tę opowiastkę głosicielom opinii, że system punktowy jest świetnym narzędziem, pozwalającym ustalać wyniki konkursów i egzaminów rzetelnie, sprawiedliwie i obiektywnie.