Co to jest?
Wielościany drżące i wielościany multistabilne
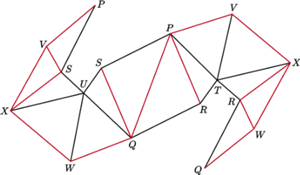
W Delcie była już mowa o ruchomych wielościanach, nazywanych też fleksorami; artykuły o nich ukazały się w 1987 i 1997 roku. Ruchomość wielościanu polega na tym, że gdybyśmy zbudowali model o sztywnych ścianach, a krawędziach poruszających się jak zawiasy, to moglibyśmy nim poruszać bez odkształcania ścian. Choć wydaje się to zaskakujące, ruchome wielościany rzeczywiście istnieją i zbudowanie takich brył, choćby z papieru, nie jest bardzo trudne.
Wielościany ruchome zostały odkryte w 1978 roku przez Roberta Connelly’ego, który skonstruował pierwszy przykład fleksora.
|

|
Drugi, prostszy przykład podał wkrótce potem Klaus Steffen.
Jak dotąd są to wszystkie znane fleksory.
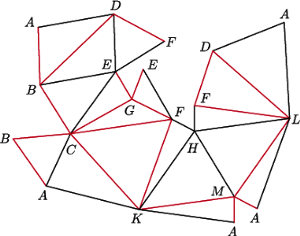
Istnieją też wielościany, które co prawda nie mogą się poruszać na tej samej zasadzie jak fleksory, mają jednak bardzo podobne własności. Ich ruch jest możliwy dzięki temu, że papier nie jest idealnie sztywny. Na jakiej zasadzie ów ruch się odbywa? Otóż najpierw należy zauważyć, że czasami wielościany o przystających ścianach i narożach mają kilka form różniących się kątami dwuściennymi. Jeśli dwie z nich są dość podobne, to możliwa jest nieniszcząca ścian zmiana z jednej pozycji na drugą, wykorzystująca elastyczność materiału, z którego jest wykonany model. Takie wielościany nazywamy multistabilnymi.
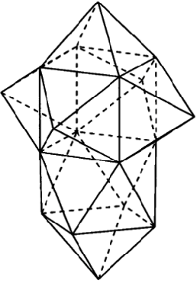
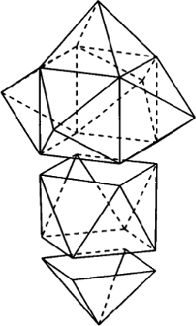
Jednym z najprostszych multistabilnych wielościanów jest dwustabilny „skaczący ośmiościan” (bistable jumping octahedron) opisany przez Waltera Wunderlicha i Caspara Schwabego w 1986 roku w pracy Eine Familie von geschlossenen gleichflächigen Polyedern, die fast beweglich sind. Wielościan ten ma dwie formy, które możemy zmieniać przez skręcenie jednej podstawy względem drugiej (patrz obrazki na następnej stronie). We wspomnianej pracy autorzy scharakteryzowali wszystkie istniejące wielościany multistabilne.

|

|
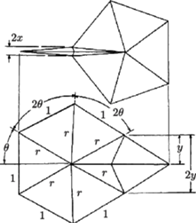
Jednakże o istnieniu wielościanów multistabilnych wiedziano trochę wcześniej. W roku 1978 opublikowany został artykuł Michaela Goldberga Unstable polyhedral structures, w którym autor opisał liczne przykłady niestandardowych wielościanów, w tym wielościan multistabilny nazwany „dwupiramidami syjamskimi” (Siamese dipyramids). Wielościan ten składa się z dwóch podwójnych piramid złączonych wspólną podstawą. Każda dwupiramida ma 10 ścian, które są trójkątami równobocznymi.
Mimo iż narysowanie siatki takiego wielościanu (ewentualnie np. w czterech
częściach) jest bardzo łatwe, to zbudowanie jego modelu jest dość trudne,
ponieważ już przy małej niedokładności zmienia się charakter bryły. Jeśli
równoboczne trójkąty zastąpimy przez równoramienne, których kąt
przy wierzchołku równy jest
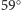 zamiast
zamiast
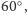 otrzymamy
dwupiramidy, które w dwóch pozycjach całkowicie się złożą. Jeśli
natomiast kąt przy wierzchołku powiększymy do
otrzymamy
dwupiramidy, które w dwóch pozycjach całkowicie się złożą. Jeśli
natomiast kąt przy wierzchołku powiększymy do
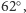 stabilne
pozycje pokryją się i otrzymamy wielościan innego rodzaju, mianowicie
dwudziestościan drżący. W artykule Goldberga była mowa również
o drżących wielościanach.
stabilne
pozycje pokryją się i otrzymamy wielościan innego rodzaju, mianowicie
dwudziestościan drżący. W artykule Goldberga była mowa również
o drżących wielościanach.
W wielościanach ruchomych możliwy jest płynny ruch między różnymi pozycjami. Wielościany multistabilne mają tylko kilka stabilnych form, a przejścia pomiędzy nimi następują w sposób skokowy. Wielościany drżące stanowią jeszcze inną grupę. Obserwując ruch modelu, nie można powiedzieć, ile stabilnych pozycji ma wielościan; tym wielościan drżący różni się od wielościanów multistabilnych, w których liczba stabilnych pozycji jest skończona.

Dwudziestościany Jessena
Można jednak za pomocą obliczeń udowodnić, że podczas ruchu drżącego wielościanu jego ściany są nieznacznie zniekształcane, więc nie jest to fleksor.
Dwudziestościan foremny jest wypukły i sztywny. Jeśli jednak sześć par
ścian o wspólnej krawędzi zastąpimy parami równoramiennych trójkątów,
tworząc niewypukły dwudziestościan, otrzymamy wielościan Jessena. Każdy
kąt dwuścienny to
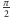 lub
lub
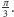 Ten wielościan może poruszać się
w niewielkim stopniu, zmieniając kąty dwuścienne wzdłuż dłuższych
krawędzi.
Ten wielościan może poruszać się
w niewielkim stopniu, zmieniając kąty dwuścienne wzdłuż dłuższych
krawędzi.
Drżący jest też wielościan (odkryty przez Paula Masona), którego wszystkie ściany są trójkątami równobocznymi. Powstaje on przez wzniesienie ostrosłupów prawidłowych czworokątnych na każdej ścianie sześcianu oraz antygraniastosłupa, który oddziela jedną z tych piramid i sześcian.
Na zakończenie warto zauważyć, że opisane powyżej zjawiska możliwe są wyłącznie w przypadku wielościanów niewypukłych. Wielościany wypukłe są sztywne, co wynika z twierdzenia Cauchy’ego o sztywności.
W 1766 roku Leonhard Euler postawił hipotezę, że każdy wielościan jest sztywny. Dopiero w 1813 roku Augustin Louis Cauchy wykazał, że jest to prawda dla wielościanów wypukłych. Cauchy w swoim dowodzie popełnił zresztą błąd, ponieważ nie rozważył wszystkich przypadków. Pomyłka Cauchy’ego pozostała niezauważona przez ponad 50 lat, jednak później dowód uzupełniono.