Kącik przestrzenny
Punkt Fermata–Torricellego
Tym razem opowiemy o punkcie Fermata–Torricellego w czworościanie...
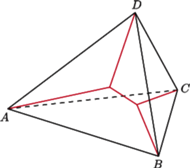
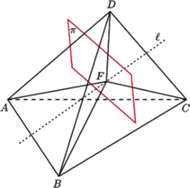
Rys. 1
Definiujemy go przez analogię do przypadku trójkąta:
Definicja. Punktem
Fermata–Torricellego nazywamy punkt
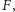 który minimalizuje sumę
odległości od wierzchołków czworościanu.
który minimalizuje sumę
odległości od wierzchołków czworościanu.
Zauważmy jednak, że łamana wyznaczona przez cztery odcinki łączące
punkt
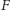 z wierzchołkami czworościanu wcale nie musi być najkrótszą
siecią odcinków łączących te wierzchołki (bardzo często krótszą sieć uzyskuje
się, biorąc łamaną złożoną z pięciu odcinków, jak na rysunku 1). Okazuje się,
że jeśli miary wszystkich kątów trójściennych przy wierzchołkach
czworościanu
z wierzchołkami czworościanu wcale nie musi być najkrótszą
siecią odcinków łączących te wierzchołki (bardzo często krótszą sieć uzyskuje
się, biorąc łamaną złożoną z pięciu odcinków, jak na rysunku 1). Okazuje się,
że jeśli miary wszystkich kątów trójściennych przy wierzchołkach
czworościanu
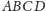 są mniejsze od
są mniejsze od
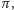 to punkt
to punkt
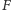 leży
wewnątrz tego czworościanu (przez miarę kąta trójściennego rozumiemy pole
powierzchni części sfery jednostkowej o środku w wierzchołku tego kąta
wyciętej przez ten kąt). Przy tym założeniu punkt ten ma szereg ciekawych
własności, opisanych poniżej.
leży
wewnątrz tego czworościanu (przez miarę kąta trójściennego rozumiemy pole
powierzchni części sfery jednostkowej o środku w wierzchołku tego kąta
wyciętej przez ten kąt). Przy tym założeniu punkt ten ma szereg ciekawych
własności, opisanych poniżej.
Twierdzenie. Jeśli punkt
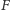 leżący wewnątrz czworościanu
leżący wewnątrz czworościanu
 minimalizuje sumę
minimalizuje sumę
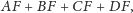 to
to
- a)
- dwusieczne
kątów płaskich
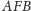 i
i
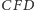 pokrywają się (tak samo dla
par kątów
pokrywają się (tak samo dla
par kątów
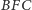 i
i
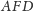 oraz
oraz
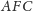 i
i
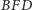 ),
),
- b)
-
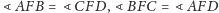 i
i
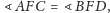
- c)
- jeśli
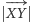 oznacza długość wektora
oznacza długość wektora
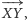 to spełniona
jest zależność
to spełniona
jest zależność
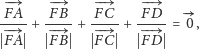
- d)
-
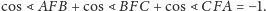
Zanim przejdziemy do dowodu twierdzenia, wprowadźmy pewien przydatny obiekt.
Definicja. Elipsoidą obrotową o ogniskach
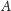 i
i
 nazywamy
powierzchnię powstałą w wyniku obrotu wokół prostej
nazywamy
powierzchnię powstałą w wyniku obrotu wokół prostej
 pewnej
elipsy o ogniskach
pewnej
elipsy o ogniskach
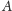 i
i
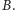
Wprost z definicji wynika następująca własność: elipsoida obrotowa
o ogniskach
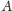 i
i
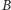 jest zbiorem wszystkich takich punktów
jest zbiorem wszystkich takich punktów
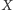 przestrzeni, że
przestrzeni, że
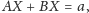 gdzie
gdzie
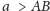 jest pewną
ustaloną liczbą rzeczywistą. Ponadto, jeśli
jest pewną
ustaloną liczbą rzeczywistą. Ponadto, jeśli
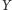 leży wewnątrz
danej elipsoidy, to
leży wewnątrz
danej elipsoidy, to
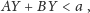 zaś jeśli
zaś jeśli
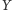 leży na
zewnątrz elipsoidy, to
leży na
zewnątrz elipsoidy, to
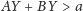 (łatwo to udowodnić, korzystając
z nierówności trójkąta).
(łatwo to udowodnić, korzystając
z nierówności trójkąta).
Poniższy fakt jest odpowiednikiem pewnej własności elipsy, opisanej np. w Delcie 2/2007 na stronie 1.

Rys. 2
Fakt 1. Załóżmy, że punkt
 leży na elipsoidzie o ogniskach
leży na elipsoidzie o ogniskach
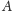 i
i
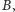 zaś
zaś
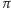 jest płaszczyzną styczną do tej elipsoidy
w punkcie
jest płaszczyzną styczną do tej elipsoidy
w punkcie
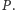 Niech
Niech
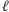 będzie prostą prostopadłą do płaszczyzny
będzie prostą prostopadłą do płaszczyzny
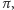 przechodzącą przez punkt
przechodzącą przez punkt
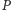 (Rys. 2). Wtedy
(Rys. 2). Wtedy
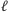 jest
dwusieczną kąta płaskiego
jest
dwusieczną kąta płaskiego
Nietrudne uzasadnienie można znaleźć analogicznie do przypadku elipsy, co pozostawiamy Czytelnikom jako zadanie, a teraz przejdziemy do dowodu głównego twierdzenia.
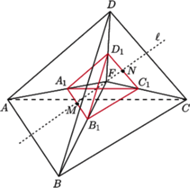
Rys. 3
Rys. 4
Dowód twierdzenia.
a) Rozważmy elipsoidę obrotową
 o ogniskach
o ogniskach
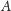 i
i
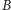 oraz elipsoidę obrotową
oraz elipsoidę obrotową
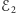 o ogniskach
o ogniskach
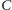 i
i
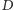 przechodzące przez punkt
przechodzące przez punkt
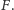 Ponieważ punkt
Ponieważ punkt
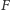 minimalizuje sumę
minimalizuje sumę
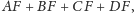 to z wcześniejszych
obserwacji wnosimy, że dane dwie elipsoidy nie mogą mieć punktów
wspólnych wewnętrznych, a więc muszą być styczne w punkcie
to z wcześniejszych
obserwacji wnosimy, że dane dwie elipsoidy nie mogą mieć punktów
wspólnych wewnętrznych, a więc muszą być styczne w punkcie
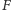 (Rys. 3). Niech
(Rys. 3). Niech
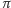 oznacza wspólną płaszczyznę styczną do tych elipsoid
w punkcie
oznacza wspólną płaszczyznę styczną do tych elipsoid
w punkcie
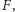 zaś
zaś
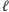 prostą prostopadłą do płaszczyzny
prostą prostopadłą do płaszczyzny
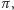 przechodzącą przez
przechodzącą przez
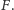 Wówczas z przytoczonego powyżej faktu
wynika, że prosta ta jest dwusieczną zarówno kąta płaskiego
Wówczas z przytoczonego powyżej faktu
wynika, że prosta ta jest dwusieczną zarówno kąta płaskiego
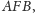 jak
i
jak
i
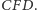 Identyczne rozumowanie przeprowadzimy dla par kątów
Identyczne rozumowanie przeprowadzimy dla par kątów
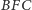 i
i
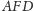 oraz
oraz
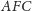 i
i
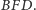
b) Wybierzmy na półprostych
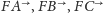 i
i
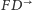 odpowiednio
takie punkty
odpowiednio
takie punkty
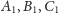 i
i
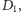 że
że
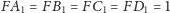 (Rys. 4). Punkt
(Rys. 4). Punkt
 jest więc środkiem sfery opisanej na czworościanie
jest więc środkiem sfery opisanej na czworościanie
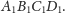 Niech ponadto prosta
Niech ponadto prosta
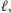 zdefiniowana jak w części a),
przecina odcinki
zdefiniowana jak w części a),
przecina odcinki
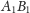 i
i
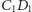 odpowiednio w punktach
odpowiednio w punktach
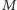 i
i
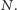 Skoro
Skoro
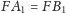 i
i
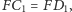 to
to
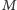 i
i
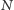 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków
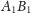 i
i
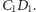 Zatem środek sfery opisanej na czworościanie
Zatem środek sfery opisanej na czworościanie
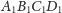 leży na prostej łączącej środki odcinków
leży na prostej łączącej środki odcinków
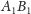 i
i
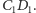 W ten sam sposób uzasadniamy, że leży on na
prostej łączącej środki odcinków
W ten sam sposób uzasadniamy, że leży on na
prostej łączącej środki odcinków
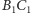 i
i
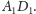 W takim
razie musi pokrywać się ze środkiem ciężkości czworościanu
W takim
razie musi pokrywać się ze środkiem ciężkości czworościanu
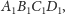 a to oznacza, że czworościan ten jest równościenny
(korzystamy tu z twierdzenia opisanego w Kąciku przestrzennym 12, w Delcie
4/2012). Stąd wnioskujemy, że
a to oznacza, że czworościan ten jest równościenny
(korzystamy tu z twierdzenia opisanego w Kąciku przestrzennym 12, w Delcie
4/2012). Stąd wnioskujemy, że

Analogicznie otrzymujemy pozostałe równości.
c) Wykorzystując zależności

widzimy, że postulowaną równość możemy przepisać w postaci
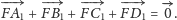 | (*) |
Jeśli
 i
i
 są środkami odcinków
są środkami odcinków
 i
i
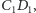 to
to

Na koniec zauważmy, że skoro
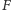 jest środkiem ciężkości
czworościanu
jest środkiem ciężkości
czworościanu
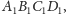 to
to
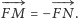
d) Wystarczy wykorzystać zależność
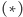 i własności iloczynu
skalarnego (np.
i własności iloczynu
skalarnego (np.
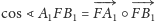 ). Uzupełnienie szczegółów
pozostawiamy Czytelnikom.
). Uzupełnienie szczegółów
pozostawiamy Czytelnikom.