Kącik przestrzenny
Sfera styczna do krawędzi czworościanu
Dla trójkąta definiujemy okrąg opisany i okrąg wpisany. Podobnie z czworościanem można związać dwie naturalne sfery: sferę przechodzącą przez wierzchołki (opisaną) oraz sferę styczną do ścian (wpisaną). Można jednak rozważać jeszcze trzecią ciekawą sferę – styczną do krawędzi.
Twierdzenie 1. Następujące warunki są równoważne:
- (a)
- istnieje sfera styczna do wszystkich krawędzi czworościanu,
- (b)
- istnieją cztery parami styczne sfery o środkach w wierzchołkach czworościanu,
- (c)
- sumy długości trzech par przeciwległych krawędzi czworościanu są równe,
- (d)
- okręgi wpisane w ściany czworościanu są parami styczne.
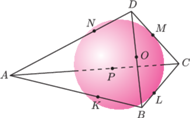
Rys. 1
Dowód. (a)
 (b). Oznaczmy przez
(b). Oznaczmy przez
 punkty styczności
danej sfery odpowiednio z krawędziami
punkty styczności
danej sfery odpowiednio z krawędziami
 Wówczas
z Najmocniejszego Twierdzenia Stereometrii (patrz Kącik 2) otrzymujemy
Wówczas
z Najmocniejszego Twierdzenia Stereometrii (patrz Kącik 2) otrzymujemy

Nietrudno teraz zauważyć, że sfery o środkach
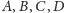 i promieniach
odpowiednio
i promieniach
odpowiednio
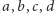 są parami styczne.
są parami styczne.
(b)
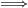 (c). Przyjmując poprzednie oznaczenia, otrzymujemy
(c). Przyjmując poprzednie oznaczenia, otrzymujemy

i podobnie
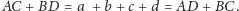

Rys. 2
(c)
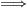 (d). Załóżmy, że okręgi wpisane w trójkąty
(d). Załóżmy, że okręgi wpisane w trójkąty
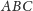 i
i
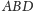 są styczne do krawędzi
są styczne do krawędzi
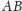 odpowiednio
w punktach
odpowiednio
w punktach
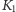 i
i
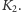 Wtedy wykorzystując zależność
Wtedy wykorzystując zależność
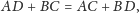 otrzymujemy
otrzymujemy

a więc
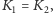 czyli okręgi te są styczne do krawędzi
czyli okręgi te są styczne do krawędzi
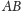 w tym
samym punkcie. W ten sam sposób stwierdzamy, że każde dwa okręgi
wpisane w ściany czworościanu są styczne.
w tym
samym punkcie. W ten sam sposób stwierdzamy, że każde dwa okręgi
wpisane w ściany czworościanu są styczne.
Rys. 3
(d)
 (a). Załóżmy, że okręgi wpisane w ściany czworościanu są
parami styczne i oznaczmy przez
(a). Załóżmy, że okręgi wpisane w ściany czworościanu są
parami styczne i oznaczmy przez
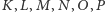 ich punkty styczności
odpowiednio z krawędziami
ich punkty styczności
odpowiednio z krawędziami
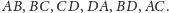 Przez środki
Przez środki
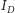 oraz
oraz
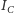 okręgów wpisanych odpowiednio w ściany
okręgów wpisanych odpowiednio w ściany
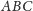 i
i
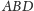 prowadzimy proste prostopadłe do tych ścian.
Ponieważ leżą one w płaszczyźnie
prowadzimy proste prostopadłe do tych ścian.
Ponieważ leżą one w płaszczyźnie
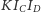 i nie są równoległe, więc
mają punkt wspólny
i nie są równoległe, więc
mają punkt wspólny
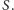 Istnieje sfera o środku
Istnieje sfera o środku
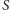 zawierająca
okręgi wpisane w ściany
zawierająca
okręgi wpisane w ściany
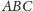 i
i
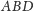 (a więc styczna do pięciu
krawędzi czworościanu zawartych w tych ścianach). Częścią wspólną tej
sfery z płaszczyzną
(a więc styczna do pięciu
krawędzi czworościanu zawartych w tych ścianach). Częścią wspólną tej
sfery z płaszczyzną
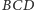 jest okrąg styczny do
jest okrąg styczny do
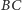 w punkcie
w punkcie
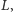 zaś do
zaś do
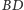 w
w
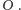 Taki okrąg jest wyznaczony
jednoznacznie, a zatem z założenia wnosimy, że musi być to okrąg wpisany
w trójkąt
Taki okrąg jest wyznaczony
jednoznacznie, a zatem z założenia wnosimy, że musi być to okrąg wpisany
w trójkąt
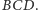 Stąd wniosek, że dana sfera jest też styczna do
krawędzi
Stąd wniosek, że dana sfera jest też styczna do
krawędzi
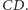
Sfera styczna do krawędzi czworościanu ma pewne cechy analogiczne do własności okręgów wpisanych w trójkąt czy czworokąt. Jedną z nich jest następująca własność, którą można nazwać odpowiednikiem twierdzenia Brianchona.
Twierdzenie 2. Sfera
 jest styczna
do wszystkich krawędzi czworościanu. Wówczas odcinki łączące punkty
styczności leżące na przeciwległych krawędziach przecinają się w jednym
punkcie.
jest styczna
do wszystkich krawędzi czworościanu. Wówczas odcinki łączące punkty
styczności leżące na przeciwległych krawędziach przecinają się w jednym
punkcie.

Rys. 4
Dowód. Oznaczmy, jak poprzednio, przez
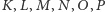 punkty
styczności sfery
punkty
styczności sfery
 z krawędziami czworościanu
z krawędziami czworościanu
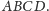 Wykażemy
najpierw, że punkty
Wykażemy
najpierw, że punkty
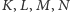 leżą na jednej płaszczyźnie.
leżą na jednej płaszczyźnie.
Jeśli
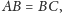 to
to
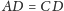 i proste
i proste
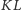 i
i
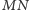 są
równoległe, więc leżą na pewnej płaszczyźnie. W przeciwnym razie istnieje
punkt
są
równoległe, więc leżą na pewnej płaszczyźnie. W przeciwnym razie istnieje
punkt
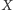 przecięcia prostych
przecięcia prostych
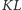 i
i
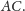 Z twierdzenia
Menelaosa otrzymujemy
Z twierdzenia
Menelaosa otrzymujemy

Zatem z twierdzenia odwrotnego do twierdzenia Menelaosa wnosimy, że punkt
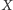 leży również na prostej
leży również na prostej
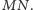 W takim razie i w tym
przypadku punkty
W takim razie i w tym
przypadku punkty
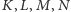 leżą na jednej płaszczyźnie.
leżą na jednej płaszczyźnie.
Odcinki
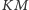 i
i
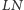 mają więc punkt wspólny
mają więc punkt wspólny
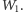 Analogicznie
stwierdzamy, że odcinki
Analogicznie
stwierdzamy, że odcinki
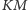 i
i
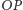 przecinają się w punkcie
przecinają się w punkcie
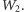 W ten sam sposób dowodzimy, że punkty
W ten sam sposób dowodzimy, że punkty
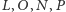 leżą
na jednej płaszczyźnie, do której należą w szczególności punkty
leżą
na jednej płaszczyźnie, do której należą w szczególności punkty
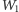 i
i
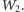 Jednak odcinek
Jednak odcinek
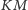 nie leży w tej płaszczyźnie,
a więc może mieć z nią co najwyżej jeden punkt wspólny. Zatem
nie leży w tej płaszczyźnie,
a więc może mieć z nią co najwyżej jeden punkt wspólny. Zatem
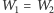 i rozważane trzy odcinki są współpękowe.
i rozważane trzy odcinki są współpękowe.
Jeśli przez
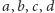 oznaczymy odpowiednio promienie sfer
o środkach
oznaczymy odpowiednio promienie sfer
o środkach
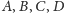 (jak w punkcie (b) Twierdzenia 1), zaś przez
(jak w punkcie (b) Twierdzenia 1), zaś przez
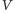 objętość danego czworościanu, to promień
objętość danego czworościanu, to promień
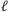 sfery stycznej
do krawędzi wyraża się wzorem
sfery stycznej
do krawędzi wyraża się wzorem

Na zakończenie dodajmy, że można rozważać sferę, która jest styczna do pewnych krawędzi oraz do przedłużeń pozostałych krawędzi czworościanu (analogicznie do okręgów dopisanych na płaszczyźnie).
Zbadanie jej własności pozostawiamy Czytelnikom.