Kącik przestrzenny
Inwersja w przestrzeni i rzut stereograficzny
Kiedy na płaszczyźnie mamy do czynienia z okręgami, to bardzo często posługujemy się rachunkiem na kątach, ponieważ znamy wiele przydatnych twierdzeń i faktów z tego zakresu. Niestety, trudno o analogiczne narzędzia w przestrzeni. Stanowi to wielki kłopot, gdy zmagamy się z zadaniami o sferach. Istnieje jednak kilka innych technik, skutecznych w zadaniach o okręgach, które działają również w przestrzeni. Są to: potęga punktu, jednokładność oraz inwersja. O tej ostatniej metodzie opowiemy w tym kąciku.
Przypomnijmy najpierw definicję i proste własności. Inwersją względem sfery
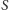 o środku
o środku
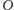 i promieniu
i promieniu
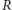 (mówi się o nich często:
środek inwersji i promień inwersji) nazywamy przekształcenie, które
przypisuje punktowi
(mówi się o nich często:
środek inwersji i promień inwersji) nazywamy przekształcenie, które
przypisuje punktowi
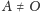 taki punkt
taki punkt
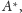 leżący na półprostej
leżący na półprostej
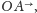 że
że
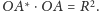 Widać podobieństwo do definicji
inwersji względem okręgu: ona wnętrze okręgu rozciąga na całe zewnętrze,
a zewnętrze wpycha do wewnątrz – inwersja względem sfery podobnie zamienia
jej wnętrze z zewnętrzem.
Widać podobieństwo do definicji
inwersji względem okręgu: ona wnętrze okręgu rozciąga na całe zewnętrze,
a zewnętrze wpycha do wewnątrz – inwersja względem sfery podobnie zamienia
jej wnętrze z zewnętrzem.
Inwersja względem sfery ma wiele przydatnych własności – oto niektóre z nich:
- inwersja jest przekształceniem odwrotnym do siebie,
- płaszczyzny i sfery przechodzą na płaszczyzny lub sfery,
- proste i okręgi przechodzą na proste lub okręgi,
- płaszczyzny i proste przechodzące przez środek inwersji przechodzą na siebie,
- płaszczyzny i proste nieprzechodzące przez środek inwersji przechodzą odpowiednio na sfery i okręgi przechodzące przez środek inwersji,
- sfery i okręgi nieprzechodzące przez środek inwersji przechodzą odpowiednio na sfery i okręgi nieprzechodzące przez środek inwersji,
- inwersja zachowuje kąty między krzywymi – kąt między krzywymi to kąt między prostymi stycznymi do tych krzywych w ich punkcie przecięcia.
Czytelnik dostrzeże, iż – niestety – nie można mówić o zachowaniu kąta między powierzchniami, gdyż pojęcie kąta między powierzchniami sensu nie ma: płaszczyzny styczne do dwóch powierzchni w różnych ich punktach wspólnych mogą tworzyć różne kąty dwuścienne.
Wygodnie jest jednak mówić o kątach między płaszczyznami, czy między sferami, czy też między płaszczyznami i sferami, bo w tych przypadkach rozwartość powstałych kątów dwuściennych nie zależy od tego, który punkt wspólny rozpatrujemy. Takie kąty są również przez inwersję zachowywane. Wykorzystamy to w następującym zadaniu, którego płaski odpowiednik jest banalnym rachunkiem na kątach.
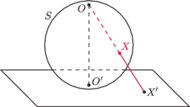
Bardzo ważnym, szczególnym przypadkiem inwersji jest tak zwany
rzut stereograficzny. Załóżmy, że punkt
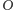 leży na sferze
leży na sferze
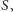 zaś płaszczyzna
zaś płaszczyzna
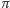 jest styczna do tej sfery w punkcie
jest styczna do tej sfery w punkcie
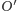 symetrycznym do
symetrycznym do
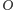 względem środka tej sfery. Obrazem
dowolnego punktu
względem środka tej sfery. Obrazem
dowolnego punktu
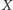 na sferze jest punkt
na sferze jest punkt
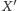 przecięcia prostej
przecięcia prostej
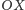 z płaszczyzną
z płaszczyzną
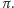 Niezwykle ważną własnością rzutu
stereograficznego jest to, że jest on niczym innym, jak inwersją o środku
Niezwykle ważną własnością rzutu
stereograficznego jest to, że jest on niczym innym, jak inwersją o środku
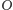 i promieniu
i promieniu
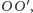 chociaż interesuje nas jedynie obraz sfery
chociaż interesuje nas jedynie obraz sfery
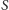 w tej inwersji. W szczególności przekształcenie to ma wszystkie
własności inwersji. Popatrzmy, jak je wykorzystać w następującym
zadaniu.
w tej inwersji. W szczególności przekształcenie to ma wszystkie
własności inwersji. Popatrzmy, jak je wykorzystać w następującym
zadaniu.
Zadania do domu
Na koniec całe mnóstwo zadań do domu.