Geometria jest nauką doświadczalną

W wielu miejscach można przeczytać czy usłyszeć, że matematyka, a zwłaszcza geometria jest nauką aksjomatyczną i wszelkie zawarte w niej fakty uzyskuje się właśnie z aksjomatów przez podporządkowane prawom logiki dowody.

Rys. 1

Rys. 2
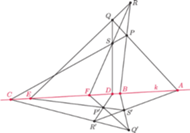
Rys. 3
I chyba nikt w rzeczywistości nie spotkał się w szkole czy na studiach z tak opisaną sytuacją. Nietrudno też byłoby uzasadnić, dlaczego tak jest, ale tu nie będziemy tego robić, tylko zajmiemy się kratką wyplecioną z wikliny albo z dość sztywnych drutów (takich, z jakich zrobione są siatki w płotach), taką jak na rysunku 1.
To, że jest ona kwadratowa, można łatwo zmienić. Jeśli pociągniemy ją (rzecz jasna, delikatnie) za przeciwległe rogi, możemy uzyskać romb (gdy ciągniemy w płaszczyźnie kratki) albo też coś w rodzaju siodła (gdy zegniemy kratkę – Rys. 2). W tym drugim przypadku powstaje pytanie, czy faktycznie w dalszym ciągu pręty wiklinowe (czy druty) mogą pozostać proste, czy też tylko nam się tak wydaje.
To, że faktycznie mogą one pozostać proste, gwarantuje twierdzenie Gallucciego:
Twierdzenie. Dane są dwie trójki prostych skośnych, w których każda prosta jednej trójki przecina każdą prostą drugiej trójki. Wówczas każda prosta przecinająca wszystkie proste jednej trójki przecina każdą prostą przecinającą wszystkie proste drugiej trójki.
Ortodoksyjny geometra powinien w tym momencie sięgnąć po aksjomaty (w wersji Euklidesa, Hilberta, Tarskiego, Krygowskiej... i wyprowadzić z nich to twierdzenie. My, oczywiście, postąpimy inaczej. Narysujemy (starannie, linijką – inne przyrządy nie będą potrzebne) rysunek, taki jak rysunek 3.
W ostatnim zdaniu najistotniejszym słowem jest narysujemy i w nim tkwi to, co uzasadni twierdzenie Gallucciego.
Nie piszę udowodni w obawie krzyku Beotów, jakby powiedział Gauss. Bardziej odważny ode mnie jest Harold S.M. Coxeter, który przedstawione dalej rozumowanie śmiało (i słusznie) nazywa dowodem.
Istotne jest też to, jak taki rysunek wykonać. I na czym polega jego ważna w poniższych rozumowaniach cecha, jaką jest stabilność.
Zaczynamy od narysowania prostej
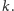 Następnie wybieramy dowolny,
nieleżący na niej punkt
Następnie wybieramy dowolny,
nieleżący na niej punkt
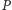 i prowadzimy przez niego dowolne trzy
proste przecinające
i prowadzimy przez niego dowolne trzy
proste przecinające
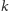 (nazwijmy otrzymane punkty przecięcia
(nazwijmy otrzymane punkty przecięcia
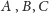 ).
).
Teraz na prostej
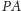 obieramy dowolnie punkt
obieramy dowolnie punkt
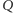 i prowadzimy
przez niego dowolne dwie proste przecinające
i prowadzimy
przez niego dowolne dwie proste przecinające
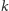 (otrzymane punkty
nazwijmy
(otrzymane punkty
nazwijmy
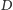 i
i
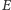 ) i nierównoległe do dotychczas narysowanych.
Ponadto oznaczmy przecięcie prostej
) i nierównoległe do dotychczas narysowanych.
Ponadto oznaczmy przecięcie prostej
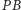 z
z
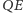 przez
przez
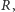 a przecięcie
a przecięcie
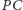 z
z
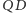 przez
przez
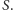 I jeszcze niech
przecięcie
I jeszcze niech
przecięcie
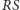 z
z
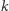 nazywa się
nazywa się
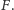
Po drugiej stronie
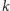 wykonamy PRAWIE taki sam rysunek. Punkt
wykonamy PRAWIE taki sam rysunek. Punkt
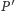 obieramy dowolnie. Na prostej
obieramy dowolnie. Na prostej
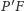 dowolnie obieramy punkt
dowolnie obieramy punkt
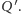 Przecięcie prostej
Przecięcie prostej
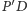 z
z
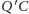 oznaczamy przez
oznaczamy przez
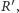 a przecięcie
a przecięcie
 z
z
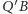 przez
przez
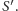 I teraz
okazuje się (proszę sprawdzić, najlepiej wielokrotnie, różnie obierając
początkowe punkty), że punkty
I teraz
okazuje się (proszę sprawdzić, najlepiej wielokrotnie, różnie obierając
początkowe punkty), że punkty
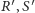 i
i
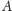 leżą na jednej
prostej.
leżą na jednej
prostej.
To, że tak się zawsze zdarzy, nazywa się właśnie stabilnością rysunku.
No właśnie: skoro tak jest zawsze, to możemy postąpić jak przyrodnicy i uznać to za prawo przyrody, a takie nie wymagają dowodów.
Spostrzeżenie o stabilności będzie nam potrzebne, abyśmy mogli uznać, że dowodząc czegoś dla tych konkretnych punktów, dowodzimy tego dla dowolnych punktów powiązanych wskazanymi wyżej zależnościami.
Teraz dokonamy całkiem realnej operacji: zegniemy pod pewnym kątem kartkę
z rysunkiem 3 wzdłuż prostej
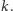 Oczywiście, wygląda to nadal tak
samo, więc możemy nadal korzystać z rysunku 3.
Oczywiście, wygląda to nadal tak
samo, więc możemy nadal korzystać z rysunku 3.
Jako jedną z trójek prostych skośnych, o których mówią założenia
twierdzenia Gallucciego, weźmy
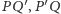 i
i
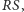 jako drugą –
jako drugą –
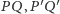 i
i
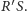 Czytelnik Spostrzegawczy zauważy, że na
rysunku nie ma tych prostych – to słuszna uwaga, ale ich narysowanie czyniłoby
rysunek zupełnie nieczytelnym (nie wiadomo byłoby, które linie przecinają się,
a które mijają), a przecież i tak o tych (niewidzialnych) prostych możemy
wiele powiedzieć.
Czytelnik Spostrzegawczy zauważy, że na
rysunku nie ma tych prostych – to słuszna uwaga, ale ich narysowanie czyniłoby
rysunek zupełnie nieczytelnym (nie wiadomo byłoby, które linie przecinają się,
a które mijają), a przecież i tak o tych (niewidzialnych) prostych możemy
wiele powiedzieć.
Możemy np. sprawdzić, że proste w każdej trójce faktycznie są skośne.
Sprawdźmy to dla
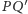 i
i
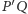 (pozostawiając pozostałe
5 sprawdzeń Czytelnikowi). Gdyby te proste leżały na jednej płaszczyźnie, na
jednej płaszczyźnie leżałyby punkty
(pozostawiając pozostałe
5 sprawdzeń Czytelnikowi). Gdyby te proste leżały na jednej płaszczyźnie, na
jednej płaszczyźnie leżałyby punkty
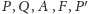 i
i
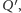 a więc
kartka nie byłaby zgięta.
a więc
kartka nie byłaby zgięta.
Możemy też sprawdzić, że każda z prostych pierwszej trójki przecina
każdą z drugiej trójki. Sprawdzimy to dla
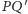 (jak poprzednio,
pozostawiając pozostałe 6 sprawdzeń Czytelnikowi) – dla wspomożenia
wyobraźni przedstawiamy obok schemat powstałej sytuacji.
(jak poprzednio,
pozostawiając pozostałe 6 sprawdzeń Czytelnikowi) – dla wspomożenia
wyobraźni przedstawiamy obok schemat powstałej sytuacji.
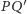 z
z
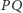 ma wspólny punkt
ma wspólny punkt
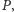 a z
a z
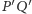 wspólny punkt
wspólny punkt
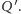 Trzecie sprawdzenie jest mniej banalne: ponieważ
Trzecie sprawdzenie jest mniej banalne: ponieważ
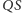 i
i
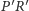 mają wspólny punkt
mają wspólny punkt
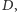 więc leżą na jednej płaszczyźnie
i na tej płaszczyźnie poprowadzone są proste
więc leżą na jednej płaszczyźnie
i na tej płaszczyźnie poprowadzone są proste
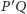 i
i
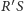 – gdyby
były przypadkiem równoległe, wystarczy jeden z punktów na tej płaszczyźnie
odrobinę przesunąć (tu korzystamy ze stabilności!).
– gdyby
były przypadkiem równoległe, wystarczy jeden z punktów na tej płaszczyźnie
odrobinę przesunąć (tu korzystamy ze stabilności!).
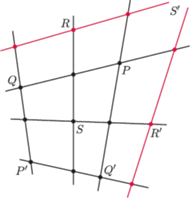
Uwaga! To nie jest rysunek, a tylko schemat pokazujący zależności. Sytuacja rzeczywista tak nie wygląda.
Tak więc (wraz z Czytelnikiem) uzyskaliśmy dziewięć punktów zaznaczonych na schemacie czarnymi kropkami.
Połóżmy teraz poprzeczkę na pierwszej trójce prostych (po angielsku
transversal jest pełnoprawnym terminem geometrycznym) przechodzącą przez
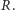
Ponieważ poprzeczka ta przecina
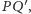 więc leży na płaszczyźnie
więc leży na płaszczyźnie
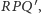 czyli na
czyli na
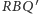 (
(
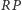 i
i
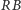 to ta sama prosta).
Analogicznie, skoro przecina
to ta sama prosta).
Analogicznie, skoro przecina
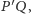 więc leży na płaszczyźnie
więc leży na płaszczyźnie
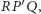 czyli
czyli
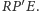 Zatem ta poprzeczka to przecięcie płaszczyzn
Zatem ta poprzeczka to przecięcie płaszczyzn
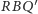 i
i
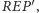 czyli prosta
czyli prosta
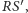 bo proste
bo proste
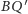 i
i
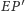 przecinają się w
przecinają się w
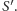
Z kolei połóżmy na drugiej trójce prostych skośnych poprzeczkę
przechodzącą przez
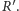 Leży ona na
Leży ona na
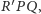 czyli
czyli
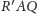 i na
i na
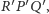 czyli
czyli
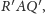 a więc – jak widać, jest prostą
a więc – jak widać, jest prostą
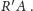 Nietrudno zauważyć, że
Nietrudno zauważyć, że
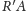 przechodzi przez
przechodzi przez
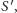 a więc poprzeczki mają punkt wspólny, mianowicie
a więc poprzeczki mają punkt wspólny, mianowicie
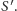
* * *
Nietrudno wyobrazić sobie, że przedstawiony wyżej dowód nie wszystkich przekonał. Formalistom brakowało zapewne odwołania nie tyle może do aksjomatów, co do jakichś powszechnie uznanych za pewne, a także za normalne, twierdzeń – takich, na które moglibyśmy się powoływać, bez obawy, że nasz egzaminator ich nie zna. Realistów mogło zrazić zagmatwanie sytuacji, w której rysujemy proste, o których uzasadniane twierdzenie się nie wypowiada, by nie rysować prostych, o których mówi – i to wszystko jakoby dla większej przejrzystości.

Ale, jako się rzekło, geometria jest nauką doświadczalną. Inżynierowie umocowali sześć zbrojonych betonowych belek w sposób spełniający założenia twierdzenia Gallucciego i, faktycznie, można było na nie kłaść następne belki, zgodnie z tym twierdzeniem. Tak powstał dach przystanku kolejowego Warszawa Ochota. Twierdzenie zatem jest prawdziwe.

Postscriptum 1 (o takich dowodach)
W podobny sposób można dowieść np. następującego twierdzenia:
Twierdzenie. Co najmniej jeden z rzutów prostokątnych środka ciężkości czworościanu na płaszczyzny jego ścian leży wewnątrz ściany.
W przeciwnym bowiem razie ten czworościan położony na stole bez końca by się przewracał.

Postscriptum 2 (o innej kratce z patyczków)
Jeśli połączymy pionowymi patyczkami dwa poziome jednakowe okręgi, a następnie obrócimy jeden z tych okręgów o jakiś kąt, to otrzymamy jedną z dwóch „górnych” sytuacji z rysunku 4 – w zależności od tego, w którą stronę będziemy obracać. Nie potrzeba specjalnej wyobraźni, by nałożyć jeden rysunek na drugi, a nawet zrealizować to, co wyjdzie, wikliną lub drutem. Taką kratką jest np. konstrukcja nośna miejskiej wieży ciśnień w Ciechanowie.
Tym, którzy z pewnym dystansem odnieśli się do całego tego tekstu, przyjemnie będzie przeczytać, że administracja Ciechanowa też z dystansem odnosi się do tej budowli.
Postscriptum 3 (może jednak trochę formalizmu)
Pewna Młoda Dama po przeczytaniu wersji wstępnej tego tekstu powiedziała, że to chyba wiele hałasu o nic, bo o obu tych powierzchniach jest mowa na I roku studiów matematycznych w ramach algebry liniowej – są to paraboloida hiperboliczna i hiperboloida jednopowłokowa, o wygodnych równaniach

Rzeczywiście, to są te powierzchnie, ale pamiętam, że – gdy byłem na I roku – stwierdzenie, że to takie gęste kratki, zrobiło na mnie wrażenie i chciałem się dowiedzieć, czy to można jakoś zobaczyć, a nie tylko wyliczyć.
Postscriptum 4 (Wielcy też o tym myśleli)
Okazuje się, że sprawa kratek nękała też Hugona Steinhausa. W Księdze Szkockiej są aż cztery postawione przez niego problemy na ten temat. Oto one.
Problem (44). Ciągła funkcja
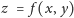 przedstawia
powierzchnię, przez której każdy punkt przechodzą dwie proste całkowicie
na niej leżące. Wykazać, że to jest paraboloida hiperboliczna. To samo bez
założenia ciągłości.
przedstawia
powierzchnię, przez której każdy punkt przechodzą dwie proste całkowicie
na niej leżące. Wykazać, że to jest paraboloida hiperboliczna. To samo bez
założenia ciągłości.
I jest dopisek z 30 lipca 1935 roku:
Ten problem pozytywnie rozstrzygnął Banach, również bez założenia
ciągłości. Dowód opiera się na spostrzeżeniu, że dowolne dwie proste tej
powierzchni albo się przecinają, albo ich rzuty na płaszczyznę
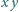 są
równoległe.
są
równoległe.
Problem (61). Wyznaczyć powierzchnie
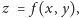 takie, że
przez każdy ich punkt przechodzą dwie przystające krzywe płaskie całkowicie
na nich leżące (mocniej: przez każdy punkt takie same).
takie, że
przez każdy ich punkt przechodzą dwie przystające krzywe płaskie całkowicie
na nich leżące (mocniej: przez każdy punkt takie same).
Dopisek Stanisława Ruziewicza (z 31 lipca 1935 roku):
Wszystkie powierzchnie obrotowe mają tę własność; nie wiadomo, czy tylko one.
Problem (78, 2 sierpnia 1935 roku). Znaleźć wszystkie
powierzchnie o następującej własności:
przez każdy punkt przechodzą dwie
krzywe całkowicie na nich leżące i przystające odpowiednio do krzywych
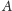 i
i
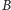 (np. tak jest na walcu).
(np. tak jest na walcu).
Tu koledzy zawiedli – brak odpowiedzi do dzisiaj.
Problem 81 (z 6 sierpnia 1935 roku) też jest na ten temat, ale jest postawiony tak zawile, że komentator w wydanej pod redakcją R. Daniela Mauldina The Scottish Book ograniczył się do podania kilku możliwych interpretacji zadanych w nim pytań i (co jest całkowitym w tej książce ewenementem) podpisał się nic nieznaczącym pseudo: Recenzent.
Po tych wszystkich wyjaśnieniach czuję się usprawiedliwiony z napisania tego tekstu, M. K.