Kącik przestrzenny
Czworościany równościenne – część I
Na płaszczyźnie, jeśli trójkąt ma równe boki, to jest równoboczny. W przestrzeni jednak czworościan, którego ściany są przystające, wcale nie musi być foremny...
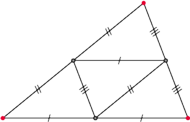
Rys. 1
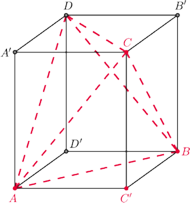
Rys. 2
Aby się o tym przekonać, wystarczy narysować dowolny nierównoboczny
trójkąt ostrokątny, podzielić go na cztery przystające trójkąty (łącząc środki
jego boków, jak na rysunku 1) i zauważyć, że otrzymujemy w ten sposób
siatkę czworościanu (dlaczego?). Inaczej, można spojrzeć na czworościan
 w prostopadłościanie
w prostopadłościanie
 (Rys. 2). Ma on
przeciwległe krawędzie równej długości, a więc jego ściany są przystające.
Takie czworościany nazywamy równościennymi. O nich opowiemy
w najbliższych dwóch odcinkach. W tym kąciku zrobimy krótki przegląd ich
własności, a następnym razem przyjrzymy się paru zastosowaniom
w zadaniach olimpijskich.
(Rys. 2). Ma on
przeciwległe krawędzie równej długości, a więc jego ściany są przystające.
Takie czworościany nazywamy równościennymi. O nich opowiemy
w najbliższych dwóch odcinkach. W tym kąciku zrobimy krótki przegląd ich
własności, a następnym razem przyjrzymy się paru zastosowaniom
w zadaniach olimpijskich.
Jednym z ważniejszych faktów związanych z czworościanem równościennym jest to, że równoległościan na nim opisany jest prostopadłościanem. To pociąga za sobą wiele ważnych konsekwencji, np. środek sfery opisanej, środek sfery wpisanej oraz środek ciężkości czworościanu są tym samym punktem – środkiem opisanego prostopadłościanu. Nietrudno również uzasadnić, że jeśli którekolwiek dwa z tych punktów się pokrywają, to czworościan jest równościenny.
Można sformułować bardzo wiele warunków równoważnych temu, że czworościan jest równościenny. Wybrane podajemy poniżej. W szczególności interesujące jest to, że wystarczy założyć równość pól ścian.
Twierdzenie. Dla dowolnego czworościanu
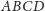 następujące warunki
są równoważne:
następujące warunki
są równoważne:
- (1)
- wszystkie ściany są przystające;
- (2)
- wszystkie ściany mają okręgi opisane o jednakowym promieniu;
- (3)
- wszystkie ściany mają równe pola;
- (4)
- wszystkie ściany mają równe obwody;
- (5)
- przeciwległe krawędzie są równe;
- (6)
- siatka czworościanu jest trójkątem ostrokątnym podzielonym na cztery przystające trójkąty; [uwaga]
- (7)
- suma kątów płaskich w każdym wierzchołku jest równa
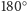 (wystarczy nawet w trzech);
(wystarczy nawet w trzech);
- (8)
-
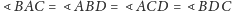 ;
;
- (9)
- równoległościan opisany na czworościanie jest prostopadłościanem;
- (10)
- rzut prostokątny czworościanu na dowolną płaszczyznę równoległą do dwóch przeciwległych krawędzi jest prostokątem;
- (11)
- wszystkie biśrodkowe są parami prostopadłe;
- (12)
- każda biśrodkowa jest prostopadła do krawędzi, które łączy;
- (13)
- pewne dwa punkty spośród następujących: środek ciężkości, środek sfery wpisanej, środek sfery opisanej, się pokrywają;
- (14)
- sfera wpisana w czworościan jest styczna do wszystkich ścian w środkach okręgów opisanych (wystarczy nawet do dwóch). [uwaga]
Zachęcamy Czytelników do samodzielnego zmierzenia się z tym twierdzeniem. Dużą część dowodu można znaleźć w artykule Waldemara Pompego („O czworościanie równościennym”, Delta 3/1994). Warto tam zajrzeć chociażby po to, żeby sprawdzić, w jakiej kolejności najwygodniej wyprowadzać jedne warunki z innych – tutaj są pogrupowane ze względu na obiekty, których dotyczą.
Czworościany równościenne są na tyle regularne, że wiele wielkości z nimi
związanych wyraża się stosunkowo prostymi, jak na czworościany, wzorami.
Przyjmując, że każda ściana takiego czworościanu jest trójkątem o bokach
długości
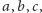 można obliczyć, że
można obliczyć, że

gdzie
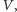
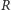 i
i
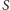 oznaczają odpowiednio objętość,
długość promienia sfery opisanej oraz pole powierzchni całkowitej. Dzieląc
potrojoną objętość przez pole, otrzymamy wzór na promień sfery wpisanej.
Można także sprawdzić, że środki sfer dopisanych leżą w wierzchołkach
prostopadłościanu opisanego na czworościanie i każda z tych sfer
ma promień dwa razy większy od promienia sfery wpisanej. Ponadto
Czytelnik Wnikliwy może znaleźć wzory na długości biśrodkowych,
środkowych i wysokości.
oznaczają odpowiednio objętość,
długość promienia sfery opisanej oraz pole powierzchni całkowitej. Dzieląc
potrojoną objętość przez pole, otrzymamy wzór na promień sfery wpisanej.
Można także sprawdzić, że środki sfer dopisanych leżą w wierzchołkach
prostopadłościanu opisanego na czworościanie i każda z tych sfer
ma promień dwa razy większy od promienia sfery wpisanej. Ponadto
Czytelnik Wnikliwy może znaleźć wzory na długości biśrodkowych,
środkowych i wysokości.
Na koniec udowodnimy jeszcze jedno ciekawe twierdzenie związane z czworościanami równościennymi.
Twierdzenie 1 (sfera dwunastu punktów). W czworościanie równościennym spodki wysokości, środki wysokości i punkty przecięcia wysokości ścian tego czworościanu leżą na jednej sferze.
Dowód. Rozważmy czworościan równościenny
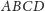 wpisany w prostopadłościan
wpisany w prostopadłościan
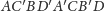 o środku
o środku
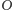 (Rys. 3). Wystarczy, jeśli
udowodnimy, że odległości punktu
(Rys. 3). Wystarczy, jeśli
udowodnimy, że odległości punktu
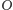 od dwunastu
rozważanych punktów są równe. Z uwagi na symetrię wystarczy
dowieść, że
od dwunastu
rozważanych punktów są równe. Z uwagi na symetrię wystarczy
dowieść, że
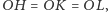 gdzie
gdzie
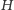 jest ortocentrum
trójkąta
jest ortocentrum
trójkąta
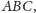
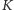 – spodkiem wysokości poprowadzonej
z punktu
– spodkiem wysokości poprowadzonej
z punktu
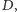 natomiast
natomiast
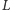 jest jej środkiem.
jest jej środkiem.
Z pierwszego zadania omawianego w kąciku 5 (a mówiłem, że to
zadanie jeszcze się przyda...) wiemy, że
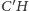 jest prostopadłe do
jest prostopadłe do
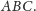 Z drugiej strony nietrudno stwierdzić, że punkt
Z drugiej strony nietrudno stwierdzić, że punkt
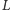 leży
na płaszczyźnie
leży
na płaszczyźnie
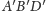 oraz
oraz
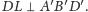 W takim razie
punkty
W takim razie
punkty
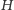 i
i
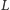 są symetryczne względem punktu
są symetryczne względem punktu
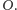 Ponadto
trójkąt
Ponadto
trójkąt
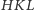 jest prostokątny, ponieważ punkty
jest prostokątny, ponieważ punkty
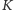 i
i
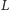 leżą
na wysokości czworościanu opuszczonej na ścianę
leżą
na wysokości czworościanu opuszczonej na ścianę
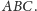 Punkt
Punkt
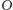 jest środkiem przeciwprostokątnej tego trójkąta, skąd wynika, że
jest środkiem przeciwprostokątnej tego trójkąta, skąd wynika, że
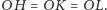
Jak widać, czworościan równościenny ma niesamowicie dużo różnych dobrych własności. Jednej rzeczy jednak na ogół nie posiada – nie ma ortocentrum. I chyba całe szczęście, bowiem jeśli już je ma, to musi być foremny. A tak mamy całą rodzinę dość regularnych czworościanów z mnóstwem ciekawych własności, których wiele odpowiedników na płaszczyźnie jest zarezerwowanych tylko dla trójkątów równobocznych.