Kącik przestrzenny
Jak wyjść z dżungli?
Każdy, kto był w dżungli lub chociaż widział ją w jakimś filmie, wie, że poruszanie się po niej jest, delikatnie mówiąc, dosyć uciążliwe. Stanowi to ogromny kłopot szczególnie wtedy, gdy ktoś się w niej zgubi i chce się jakoś wydostać. Nie dość, że nie wiadomo, w jakim kierunku iść, to w ogóle ciężko jest nam pokonywać przeszkody (a rozwiązania siłowe, takie jak maczeta, niewiele dają). Istnieje następujące zalecenie: wystarczy znaleźć strumień (co zresztą wcale nie musi być łatwe), a potem liczyć na to, że zaprowadzi nas on do większej rzeki, a ta, być może, do morza.
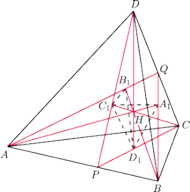
Rys. 1 Nawet jeśli narysujemy tylko płaszczyzny
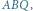
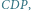
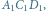
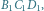 to i tak rysunek jest bardzo nieczytelny.
to i tak rysunek jest bardzo nieczytelny.
Podobnie jest z zadaniem pochodzącym z finału olimpiady rosyjskiej z 1994 roku – oto ono:
Zadanie. Punkt
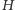 przecięcia wysokości
przecięcia wysokości
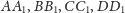 czworościanu
czworościanu
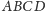 leży wewnątrz tego czworościanu oraz jest środkiem sfery
wpisanej w czworościan
leży wewnątrz tego czworościanu oraz jest środkiem sfery
wpisanej w czworościan
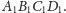 Dowieść, że czworościan
Dowieść, że czworościan
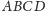 jest foremny.
jest foremny.
Rysunek do tego zadania jest potworną plątaniną kresek – zupełnie nic nie widać. Może się wydawać, że znajdujemy się w samym środku dżungli... Okazuje się jednak, że wystarczy uczynić jedno drobne spostrzeżenie (czyli wypatrzeć strumień), które zaprowadzi nas łatwo do celu. Zatem do dzieła!
Z poprzednich kącików wiemy już, że warto zrobić sobie kilka rysunków, na
których będą tylko potrzebne nam kreski. No właśnie, tylko co narysować,
a czego nie? Wydaje się, że potrzebujemy stosunkowo dużo kresek (Rys. 1)
i właściwie nie widać, jak wykorzystać fakt, że punkt
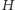 jest
środkiem sfery wpisanej w czworościan
jest
środkiem sfery wpisanej w czworościan
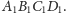 Można tylko
zobaczyć, że płaszczyzny wyznaczone przez dwie wysokości czworościanu
Można tylko
zobaczyć, że płaszczyzny wyznaczone przez dwie wysokości czworościanu
 są płaszczyznami dwusiecznymi odpowiednich kątów
dwuściennych czworościanu
są płaszczyznami dwusiecznymi odpowiednich kątów
dwuściennych czworościanu
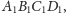 ale co zrobić potem?
ale co zrobić potem?
Próbujmy więc dalej. Pamiętamy również, że gdy nie wiemy, co zrobić w przestrzeni, to warto rozwiązać analogiczne zadanie na płaszczyźnie. No to rozwiążmy! Zakładamy, że ortocentrum danego trójkąta ostrokątnego jest środkiem okręgu wpisanego w trójkąt utworzony przez spodki jego wysokości i wtedy... No właśnie, niestety, na płaszczyźnie jest inaczej, bowiem zachodzi łatwe do udowodnienia
Rys. 2
Twierdzenie 1. Punkt
 przecięcia wysokości
przecięcia wysokości
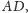
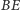 i
i
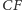 dowolnego trójkąta ostrokątnego jest
środkiem okręgu wpisanego w trójkąt
dowolnego trójkąta ostrokątnego jest
środkiem okręgu wpisanego w trójkąt
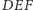 (Rys. 2).
(Rys. 2).
Tym razem nie uda się nam „zejście na ziemię”. Zadanie wydaje się niemożliwe do rozwiązania. Ale przecież nie ma rzeczy niemożliwych, są tylko takie, których jeszcze nie potrafimy!
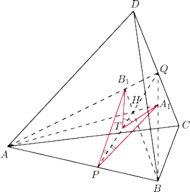
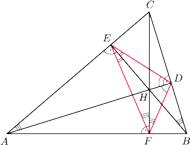
Rys. 3
Mimo wszystko może ten płaski odpowiednik zadania do czegoś nam się przyda.
Przyjrzyjmy się dokładniej płaszczyźnie
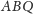 na rysunku 3.
Wysokości czworościanu
na rysunku 3.
Wysokości czworościanu
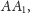
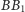 oraz odcinek
oraz odcinek
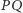 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego
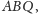 a
a
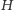 jego ortocentrum. Korzystając teraz z twierdzenia 1, wnosimy, że
jego ortocentrum. Korzystając teraz z twierdzenia 1, wnosimy, że
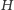 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt
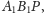 czyli
w szczególności
czyli
w szczególności
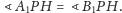 Krawędź
Krawędź
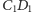 leży
w płaszczyźnie
leży
w płaszczyźnie
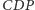 i przecina odcinek
i przecina odcinek
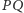 w punkcie
w punkcie
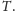 Intuicja podpowiada nam, że, być może, zachodzi równość
Intuicja podpowiada nam, że, być może, zachodzi równość
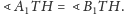 Może miary tych kątów płaskich są równe
miarom odpowiednich kątów dwuściennych między płaszczyzną
Może miary tych kątów płaskich są równe
miarom odpowiednich kątów dwuściennych między płaszczyzną
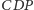 a płaszczyznami
a płaszczyznami
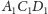 i
i
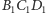 (których
równość łatwo jest uzasadnić)? Niestety, w ogólnej sytuacji wcale nie musi
tak być. Czyżby intuicja nas zawiodła? Otóż nie – można znaleźć
uzasadnienie. Mianowicie, jeśli płaszczyzna
(których
równość łatwo jest uzasadnić)? Niestety, w ogólnej sytuacji wcale nie musi
tak być. Czyżby intuicja nas zawiodła? Otóż nie – można znaleźć
uzasadnienie. Mianowicie, jeśli płaszczyzna
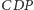 jest płaszczyzną
dwusieczną kąta dwuściennego między płaszczyznami
jest płaszczyzną
dwusieczną kąta dwuściennego między płaszczyznami
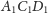 i
i
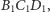 to płaszczyzny te są symetryczne względem
to płaszczyzny te są symetryczne względem
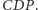 Ponadto
z prostopadłości płaszczyzn
Ponadto
z prostopadłości płaszczyzn
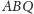 i
i
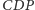 wynika, że również
proste
wynika, że również
proste
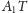 i
i
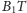 są symetryczne względem płaszczyzny
są symetryczne względem płaszczyzny
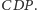 To zaś oznacza, że
To zaś oznacza, że
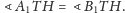 W takim razie
trójkąty
W takim razie
trójkąty
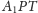 i
i
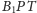 są przystające, skąd wniosek, że
są przystające, skąd wniosek, że
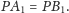 Strumień został więc znaleziony! Dalej będzie już
z górki.
Strumień został więc znaleziony! Dalej będzie już
z górki.
Teraz w nietrudny sposób można wykazać, że
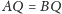 (dowód
pozostawiamy Czytelnikowi), a w takim razie też
(dowód
pozostawiamy Czytelnikowi), a w takim razie też
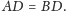 Analogicznie
dowodzimy, że dowolne dwie sąsiednie krawędzie są równe, co kończy dowód.
Nie ma rzeczy niemożliwych: każde, nawet najbardziej skomplikowane
zadanie da się rozwiązać!
Analogicznie
dowodzimy, że dowolne dwie sąsiednie krawędzie są równe, co kończy dowód.
Nie ma rzeczy niemożliwych: każde, nawet najbardziej skomplikowane
zadanie da się rozwiązać!
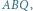
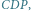
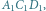
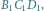 to i tak rysunek jest bardzo nieczytelny.
to i tak rysunek jest bardzo nieczytelny.