Kącik przestrzenny
Trzy rozwiązania pewnego zadania
W tym kąciku zajmiemy się pewnym zadaniem o czworościanie foremnym, o którym, między innymi, miałem okazję opowiadać na XLVI Szkole Matematyki Poglądowej pod hasłem Podejście niestandardowe.
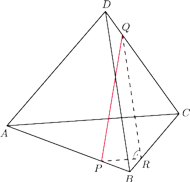
Zadanie. Dany jest czworościan foremny o krawędzi długości
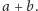 Punkty
Punkty
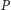 i
i
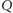 leżą na krawędziach
leżą na krawędziach
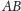 i
i
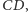 przy czym
przy czym
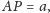
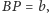
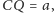
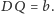 Znaleźć
długość odcinka
Znaleźć
długość odcinka
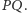
Zadanie jest szkolne, a więc zobaczmy, jak wygląda typowo szkolny sposób rozwiązywania.
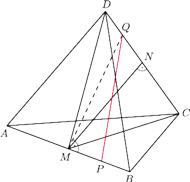
Sposób I – za pomocą twierdzenia Pitagorasa. Oznaczmy przez
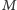 i
i
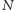 środki krawędzi
środki krawędzi
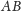 i
i
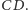 Odcinki
Odcinki
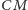 i
i
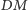 są wysokościami trójkątów równobocznych
są wysokościami trójkątów równobocznych
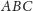 i
i
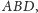 a więc
ich długości są równe
a więc
ich długości są równe
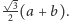 Trójkąt
Trójkąt
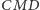 jest więc
równoramienny, zatem jego środkowa
jest więc
równoramienny, zatem jego środkowa
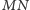 jest jednocześnie
jego wysokością i z twierdzenia Pitagorasa
obliczymy, że
jest jednocześnie
jego wysokością i z twierdzenia Pitagorasa
obliczymy, że
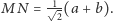 Jeśli
Jeśli
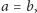 to wiemy już,
że
to wiemy już,
że
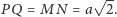 Dalej przyjmijmy dla
ustalenia uwagi, że
Dalej przyjmijmy dla
ustalenia uwagi, że
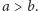 Trójkąt
Trójkąt
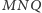 jest prostokątny,
a skoro
jest prostokątny,
a skoro
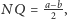 to znów korzystając z twierdzenia Pitagorasa,
obliczymy, że
to znów korzystając z twierdzenia Pitagorasa,
obliczymy, że

Płaszczyzna
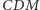 jest płaszczyzną symetralną odcinka
jest płaszczyzną symetralną odcinka
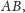 a więc jest do niego prostopadła. To samo dotyczy dowolnej
prostej w niej zawartej, skąd wniosek, że
a więc jest do niego prostopadła. To samo dotyczy dowolnej
prostej w niej zawartej, skąd wniosek, że
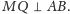 Z twierdzenia
Pitagorasa dla trójkąta prostokątnego
Z twierdzenia
Pitagorasa dla trójkąta prostokątnego
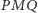 dostajemy
dostajemy

skąd
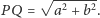
Rachunki dość uciążliwe, ale wynik podejrzanie ładny
 Spróbujmy
więc innego podejścia. Doświadczony uczestnik olimpiad, jak również
Czytelnik Uważny, spojrzałby na to w następujący sposób.
Spróbujmy
więc innego podejścia. Doświadczony uczestnik olimpiad, jak również
Czytelnik Uważny, spojrzałby na to w następujący sposób.
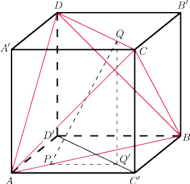
Sposób II – za pomocą wpisania czworościanu foremnego w sześcian.
Na czworościanie
 opiszmy sześcian
opiszmy sześcian
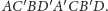 Długość
jego krawędzi jest równa
Długość
jego krawędzi jest równa
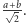 Niech
Niech
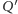 będzie takim punktem
na odcinku
będzie takim punktem
na odcinku
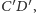 że
że
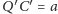 i
i
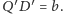 Wtedy odcinek
Wtedy odcinek
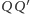 jest prostopadły do podstawy
jest prostopadły do podstawy
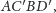 a jego długość
jest równa długości krawędzi sześcianu, czyli
a jego długość
jest równa długości krawędzi sześcianu, czyli
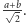 Znowu, jeśli
Znowu, jeśli
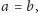 to punkt
to punkt
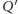 pokrywa się z punktem
pokrywa się z punktem
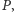 a więc
odcinek
a więc
odcinek
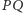 pokrywa się z
pokrywa się z
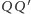 – stąd
– stąd
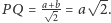 W przeciwnym
przypadku trójkąt
W przeciwnym
przypadku trójkąt
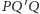 jest prostokątny. Korzystając np. z twierdzenia
Talesa, możemy obliczyć, że
jest prostokątny. Korzystając np. z twierdzenia
Talesa, możemy obliczyć, że
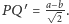 Stosując teraz twierdzenie
Pitagorasa dla trójkąta
Stosując teraz twierdzenie
Pitagorasa dla trójkąta
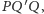 otrzymujemy
otrzymujemy

i znów
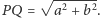
Tym razem rachunki były krótsze, ale nadal trzeba coś obliczyć, a poza tym
w obu rozwiązaniach obliczenia nie obejmują przypadku
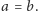 Pokażemy
więc sposób, który daje wynik natychmiast i bez rozpatrywania dwóch
przypadków.
Pokażemy
więc sposób, który daje wynik natychmiast i bez rozpatrywania dwóch
przypadków.
Sposób III – za pomocą... chytrego, niestandardowego pomysłu.
Niech
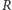 będzie takim punktem leżącym na krawędzi
będzie takim punktem leżącym na krawędzi
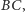 że
że
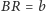 i
i
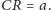 Trójkąty
Trójkąty
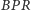 i
i
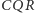 są równoboczne,
a stąd wynika, że
są równoboczne,
a stąd wynika, że
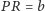 i
i
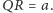 Z twierdzenia odwrotnego
do twierdzenia Talesa wnioskujemy, że
Z twierdzenia odwrotnego
do twierdzenia Talesa wnioskujemy, że
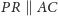 i
i
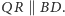 Ale
krawędzie
Ale
krawędzie
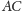 i
i
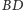 czworościanu
czworościanu
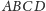 są prostopadłe
(dlaczego?), skąd wnioskujemy, że trójkąt
są prostopadłe
(dlaczego?), skąd wnioskujemy, że trójkąt
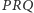 jest prostokątny.
Twierdzenie Pitagorasa daje więc wynik
jest prostokątny.
Twierdzenie Pitagorasa daje więc wynik