Kącik przestrzenny
Kąty płaskie w przestrzeni
Tym razem opowiemy o kątach w przestrzeni, a dokładniej o tym, jak rozwiązywać zadania zawierające nierówności miar kątów w przestrzeni. W zadaniach pojawiają się dwa typy kątów – płaskie i dwuścienne. Ten odcinek poświęcimy kątom płaskim, a o dwuściennych opowiemy następnym razem.
W zadaniach z nierównościami dotyczącymi kątów płaskich nie ma wielkiej filozofii, należy zapamiętać jedno ważne twierdzenie i jeden prosty wniosek – właśnie od nich rozpoczniemy.
Twierdzenie 1. W dowolnym kącie trójściennym każdy z kątów płaskich jest mniejszy od sumy dwóch pozostałych kątów.
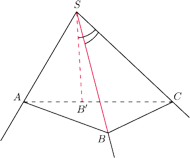
Rys. 1
Dowód. Mamy wykazać, że
w kącie trójściennym
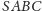o wierzchołku
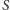zachodzi
nierówność
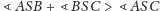(Rys. 1). Przyjmijmy, że
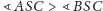(w przeciwnym przypadku nie ma czego
dowodzić). Niech
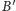będzie punktem leżącym wewnątrz ściany
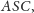takim że
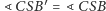i
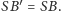Można, oczywiście, przyjąć, że punkt
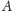leży
na prostej
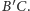Wtedy z nierówności trójkąta mamy
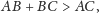skąd otrzymujemy, że
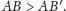Trójkąty
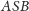i
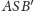mają dwa boki równe, a trzeci w pierwszym
jest większy, skąd wniosek, że
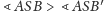(np. na mocy
twierdzenia cosinusów). To zaś dowodzi naszej nierówności.
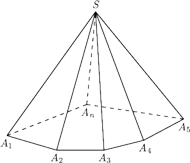
Rys. 2
Dowód. Przyjmijmy, że
dany kąt bryłowy o wierzchołku
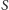tworzy
ścian. Niech
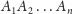będzie wielokątem powstałym z przecięcia
ścian tego kąta płaszczyzną. Korzystając z poprzedniego twierdzenia dla
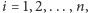dostajemy nierówności
Dodając je
wszystkie stronami, otrzymamy po lewej stronie
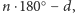gdzie
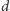oznacza sumę kątów płaskich danego kąta bryłowego, a po prawej
sumę kątów wielokąta
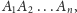czyli
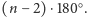Stąd
wynika, że
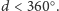
Dowód twierdzenia 2 wskazuje, że czasem, zamiast patrzeć bezpośrednio na interesujący nas kąt, warto spojrzeć na dwa pozostałe kąty trójkąta i dla nich stosować twierdzenie 1. Wykorzystamy naszą wiedzę do rozwiązania następującego zadania.
Jak nietrudno zauważyć, z powyższego zadania wynika ogólniejszy rezultat, który był treścią jednego z zadań na III Austriacko-Polskich Zawodach Matematycznych:
