Zdarza się bowiem, że rozwiązując problem przestrzenny, nie wiemy, jak się do niego zabrać, natomiast widzimy, że można sformułować analogiczne zadanie na płaszczyźnie. Czasem rozwiązanie takiego zadania na płaszczyźnie może nam podpowiedzieć, co zrobić w przestrzeni.

Nietrudno zauważyć, że wierzchołki realizują maksimum, a intuicja podpowiada nam, że pewnie tylko one. Spróbujmy więc sformułować, a następnie rozwiązać, analogiczne zadanie na płaszczyźnie:

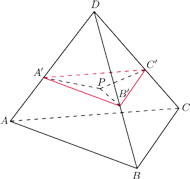
Przejdźmy do sytuacji trójwymiarowej. Przyjmijmy, że 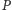leży wewnątrz czworościanu foremnego 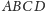o krawędzi 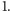 Wykorzystajmy naszą wiedzę o wersji płaskiej. Tym razem, zamiast prostej, poprowadźmy płaszczyznę równoległą do 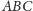 przechodzącą przez punkt 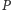 i przecinającą krawędzie 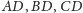odpowiednio w punktach 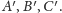Podobnie jak w wersji płaskiej, czworościan 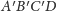jest foremny, więc 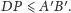Znów z nierówności trójkąta otrzymamy

więc dostajemy

Ostatnia nierówność wynika z zastosowania wersji płaskiej dla trójkąta

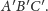
W tym zadaniu rozwiązanie analogicznego problemu płaskiego nie tylko podpowiedziało nam, jak znaleźć rozwiązanie wersji przestrzennej, ale nawet okazało się elementem dowodu.

Zadanie na pierwszy rzut oka wygląda dość przerażająco. Ale to tylko pozory, tak naprawdę jest dosyć łatwe. Żeby mieć lepszy ogląd, najpierw rozwiążmy wersję płaską:

Teraz rozwiązanie zadania w wersji przestrzennej nie powinno sprawić już żadnych problemów.

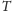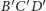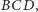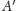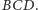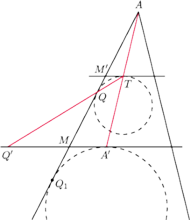
Istotnie, prowadząc przez płaszczyznę równoległą do stwierdzamy, że punkt jest punktem styczności sfery dopisanej do czworościanu ze ścianą Dla wygody i przejrzystości rozumowania rozważmy przekrój czworościanu 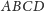oraz dwóch rozważanych sfer płaszczyzną 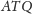(Rys. 4) – cała reszta jest niepotrzebna, gdyż wersja płaska wyrobiła nam pewne intuicje. Punkt 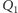styczności sfery dopisanej z płaszczyzną 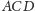leży na prostej 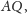należy więc do przekroju. Niech ponadto 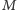 i 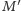będą odpowiednio punktami przecięcia prostej z prostą 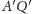i prostą do niej równoległą przechodzącą przez punkt 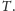Postępując analogicznie jak w wersji płaskiej, otrzymamy kolejno równości:

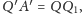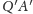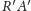skąd natychmiast wynika, że czyli jest równe długości odcinka stycznego do obu sfer. W ten sam sposób dowodzimy, że tę własność mają odcinki  i

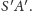
Zadanie to jest kolejnym przykładem, jak duże znaczenie w zadaniach przestrzennych ma czytelny rysunek zawierający tylko potrzebne rzeczy. A wersja płaska pomogła nam zdecydować, co tak naprawdę jest potrzebne do rozwiązania.