Kącik przestrzenny
Najmocniejsze twierdzenie stereometrii
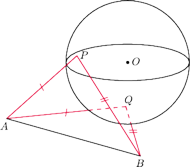
Rozpocznijmy od sformułowania tytułowego twierdzenia (łatwy dowód pozostawiamy Czytelnikowi).
Twierdzenie 1. Dana jest sfera
 oraz takie punkty
oraz takie punkty
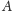 i
i
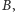 że prosta
że prosta
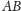 jest rozłączna ze sferą
jest rozłączna ze sferą
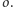 Prowadzimy dwie
płaszczyzny przechodzące przez punkty
Prowadzimy dwie
płaszczyzny przechodzące przez punkty
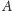 i
i
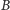 styczne do
sfery
styczne do
sfery
 w punktach
w punktach
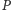 i
i
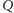 . Wówczas
. Wówczas
- a)
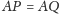
- b) trójkąty
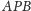 i
i
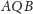 są przystające
są przystające
Z części a) otrzymujemy, że jeśli do dwóch danych sfer poprowadzimy dwie wspólne styczne zewnętrzne, to odcinki łączące punkty styczności zawarte w tych stycznych będą równej długości (dlaczego?).
Okazuje się, że te proste fakty mogą prowadzić do bardzo ciekawych i niebanalnych wniosków. Przyjrzyjmy się kilku przykładom.
Warto zapamiętać ten fakt, bo na pierwszy rzut oka jest dość zaskakujący (i, niestety, mało znany), a przydaje się w wielu miejscach. Czytelnikom pozostawiamy dowód, że analogiczna własność zachodzi również dla sfery dopisanej, jak i w przypadkach, gdy jeden lub dwa wierzchołki uciekną do nieskończoności.
Nastepne zadanie pochodzi z olimpiady OM 54-III-5. Sięgając do broszurki z tej olimpiady, widzimy, że zadanie to rozwiązały zaledwie 3 osoby, jedna w połowie, a aż 122 prace zostały ocenione na 0 punktów! Jednakże zadanie to, jak za chwilę zobaczymy, jest bardzo łatwe – wystarczy zauważyć kilka par trójkątów przystających i porachować troszkę na kątach.
Dlaczego więc tak proste zadanie sieje takie spustoszenie na finale? Częstym błędem wielu olimpijczyków jest rysowanie wszystkich rzeczy na jednym rysunku. Na powyższym przykładzie przekonaliśmy się, jak dużo może dać zrobienie kilku rysunków i zaznaczenie na każdym z nich jedynie pewnych elementów! Być może brakuje też wiary, że do tego typu zadań wystarczają jedynie te prościutkie fakty przytoczone na początku. Pamiętajcie: wiara czyni cuda!