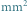Vilfredo Pareto (1848-1923), włoski arystokrata i ekonomista, zauważył, co i tak było widoczne dla zwykłych ludzi, że dobrobyt i bogactwo wcale nie są równomiernie rozłożone wśród obywateli. Obiegowe powiedzenie mówiące, że 80% majątku znajduje się w rękach zaledwie 20% ludzi, przełożył on na następującą formułę matematyczną:

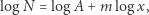(1)

gdzie 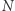oznacza liczbę osób, których dochód nie przekracza 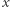jednostek, natomiast 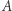i 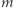są pewnymi stałymi charakterystycznymi dla kraju. Ponadto w swoim trzytomowym dziele Cours d'économie politique, (1896-1897) Pareto twierdził, że prawo to obowiązywało zawsze i we wszystkich krajach. Badania empiryczne, prowadzone sporadycznie do dzisiaj, sugerują, że tak jest w rzeczywistości. Zauważmy, że formułę (1) można przedstawić w równoważnej formie jako

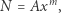(2)

czyli jako krzywą potęgową. Postać pierwsza, zwana prawem Pareto, ma jednakże tę zaletę, że we współrzędnych 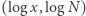przedstawia linię prostą.

Zmieńmy temat. W latach trzydziestych ubiegłego stulecia profesor lingwistyki z uniwersytetu Harvarda, niejaki George Kingsley Zipf (1902-1950), spostrzegł inną zależność. Otóż jeśli weźmie się dostatecznie długi tekst, np. rocznik gazety codziennej New York Times, i wypisze z niego wszystkie spotkane tam wyrazy oraz zliczy, ile razy każdy z nich wystąpił, to z tego da się coś wykombinować. Tę gigantyczną pracę wykonały najlepsze osiągalne ówcześnie bioprocesory, czyli po prostu studenci Zipfa. Ci z Czytelników, którzy znają język angielski, nie będą zapewne zdziwieni, że absolutnym rekordzistą okazało się słówko the; pozostali natomiast przynajmniej rozumieją dlaczego G.K. Zipf był uważany za ekscentryka. Co robimy dalej z plonem całej tej pracy? Otóż każdemu słowu nadajemy rangę, czyli numer, tym niższy, im częściej dane słowo występuje w badanym tekście. Jak na zawodach sportowych: najlepszy zawodnik zajmuje na podium miejsce z numerem 1, a inni - miejsca z numerami wyższymi. Możemy teraz sporządzić wykres, a właściwie histogram: na osi odkładamy rangi, natomiast rzędne to liczba wystąpień wszystkich słów o danej randze. Zipf zaobserwował tutaj odwrotną proporcjonalność, tj. 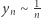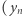to liczba słów o randze n), czyli tak samo, jak stanowi prawo Pareto (2) w szczególnym przypadku, kiedy wykładnik potęgi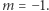

Oczywiście wykładnik 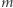wywiedziony ze zgromadzonych danych zwykle nie będzie dokładnie równy -1, bo przecież bioprocesory Zipfa musiały zrobić co najmniej kilka błędów. Ale będzie bliski liczby -1, cokolwiek słowo bliski oznacza dla profesora lingwistyki. W późniejszych latach Zipf wykonał jeszcze ranking dużych miast amerykańskich (odpowiednio do wielkości ich populacji) i, ku swemu zdziwieniu, znowu otrzymał z wykresu wykładnik 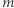bliski -1. Odtąd odwrotna proporcjonalność bywa nazywana prawem Zipfa. Sam autor wolał nazwać odkryte przez siebie prawo empiryczne zasadą najmniejszego wysiłku. Nazwa ta prawdopodobnie przyszła mu do głowy dlatego, że słowa o najniższych rangach są jednocześnie krótkie (przyimki i spójniki), natomiast te z wysoką rangą - długie. Ciekawe, że podobny wynik uzyskuje się w odniesieniu do całych fraz, np. nazywam się, co to takiego i podobnych. Znowu otrzymuje się prawo Zipfa, a frazy występują tym rzadziej, im są dłuższe.

Dygresja: ranking jest niezwykle sprytną sztuczką wymyśloną przez statystyków do obróbki danych niemających dobrych wartości liczbowych, takich jak np. kolory czy typy antropologiczne. Obiektom tego rodzaju trudno przypisać jakieś konkretne wartości liczbowe, ale można nadać im rangi. Oczywiście nadawanie rang nie jest procedurą, którą można wykonać w jeden, jedyny sposób - i dlatego zawsze musimy powiedzieć, jak to zrobiliśmy. Ściśle rzecz biorąc, prawo Zipfa, w odróżnieniu od prawa Pareto, dotyczy właśnie rang, o czym często się zapomina.

Podobne badania prowadzono wielokrotnie w różnych krajach. Na przykład w Japonii sporządzono ranking gruntów wystawionych na sprzedaż w ciągu kilku lat. Zarówno ich ceny, jak i wielkości powierzchni spełniały prawo Zipfa, podobnie jak dochody ludności - prawo Pareto. Zbadano także rozkład dochodów firm w różnych branżach - i stale wychodziło to samo: prawo Pareto-Zipfa. Zupełnie nieoczekiwanie okazało się, że na obszarach dawnego ZSRR oraz Chin rankingi miast wyraźnie nie podporządkowują się prawu Zipfa! Wiemy, że w tych krajach ruchy migracyjne były przez wiele lat regulowane administracyjnie, zakłócając tym samym naturalne zjawiska demograficzne. Dla równowagi informujemy, że w roku 2004 stwierdzono stosowalność prawa Zipfa do zupełnie specyficznego języka, jakim jest zapis nutowy. Wydawać by się zatem mogło, że Zipf odkrył jakieś bardzo ogólne prawo natury. Tylko jakie?

Hmmm... Dobre pytanie. Okazało się bowiem, że tzw. małpi tekst, czyli wynik czysto przypadkowego klepania w klawiaturę, także spełnia prawo Zipfa! Jest to wynik zupełnie pewny, bo w tym przypadku można właściwy wykładnik precyzyjnie obliczyć, nie tylko zbadać empirycznie.

Nauki ścisłe nie są aż tak niefrasobliwe pod względem rachunków jak Pareto, który bez większych problemów logarytmował liry, franki czy dolary. My umiemy logarytmować jedynie liczby. Ranga - to właśnie zwykła liczba i zapewne dlatego prawo Zipfa, choć ograniczone do ustalonej wartości wykładnika potęgi, zyskało na popularności jako lepiej osadzone w rzeczywistości matematycznej. Te problemy rozważał matematyk francuski Benoî t Mandelbrot (1924-2010), ten od fraktali. Postanowił on jakoś "wyprowadzić" prawo Zipfa, lub przynajmniej podać jego najbardziej ogólną postać. Chciałoby się też, aby prawo - skoro wydaje się tak fundamentalne - opisywało także wielkości o charakterze ciągłym. Wynik Mandelbrota z 1977 roku to:

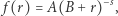(3)

gdzie 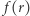oznacza częstość występowania obiektów (inaczej mówiąc: prawdopodobieństwo) o randze 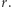Jeśli 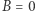oraz dodatkowo 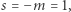to wzór ten opisuje prawo Zipfa. Rezygnacja ze sztywno ustalonej wartości wykładnika prowadzi nas do prawa Pareto. Wciąż jednakże nie opisujemy zmiennych czy wielkości mianowanych typu ciągłego. Dla takich przypadków powinniśmy raczej pisać

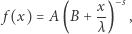(4)

gdzie 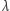oznaczałaby jakiś charakterystyczny rozmiar ( "skalę") wielkości 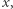a dzięki jej wprowadzeniu uzyskalibyśmy wyrażenie poprawne pod względem matematycznym - ewentualne jednostki, np. sekundy, skracają się i podstawa potęgi pozostaje liczbą niemianowaną. Na przykład w problemach związanych z lotnictwem przyjęło się wyrażać przyspieszenia (przeciążenia) w jednostkach 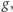choć przyspieszenie ziemskie 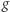wcale nie jest "okrągłą" liczbą. Chciałoby się też, aby wielkość 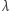miała jasną interpretację fizyczną. I tak bywa: ciepło właściwe w okolicy przejścia fazowego drugiego rodzaju dobrze opisuje się równaniem (4), jeśli 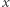oznacza temperaturę, 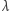jest temperaturą przejścia 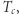a stała 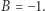Biegli w termodynamice nazywają stałą wykładnikiem krytycznym.

Wreszcie dochodzimy do sedna rzeczy. W zjawiskach, które są dobrze opisywane potęgowym rozkładem prawdopodobieństwa, czyli 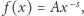takiej charakterystycznej skali 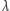nie daje się wprowadzić w sposób naturalny, w tym samym sensie, w jakim naturalną miarą kątów są radiany. Jakieś jednostki oczywiście można wprowadzić, ale gdyby ktoś na przykład chciał używać jednostek trzykrotnie większych niż nasze ulubione, to jego opis różniłby się od naszego tylko wartością stałej 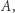natomiast wykładnik pozostałby taki sam. O zjawiskach tego rodzaju mówimy, że nie mają one charakterystycznej skali.

Zipf i jego naśladowcy zademonstrowali kilka przykładów zjawisk SF. Czy istnieją także inne? I czy znajomość prawa Pareto-Zipfa-Mandelbrota jest do czegokolwiek przydatna w codziennej rzeczywistości? W ostatnich latach obserwujemy dosłownie wybuch aktywności naukowej, której celem jest wykazanie, że kolejne zachowanie Przyrody jest typu SF. W literaturze znajdujemy wiele różnych wykresów, które pokazują, że rozkład potęgowy zdarzeń jest dobrym opisem rzeczywistości w szerokim zakresie, z reguły obejmującym kilka rzędów wielkości. Odchyłki od linii prostej (w skali logarytmicznej) najczęściej tłumaczy się skończoną wielkością próbki podlegającej badaniom.

Przedstawimy teraz niektóre z tych badań i ich wyniki.

Piłka nożna, strzelone gole - fizycy brazylijscy ustalili, że ranking piłkarzy z narodowych lig czterech krajów: Włoch, Wielkiej Brytanii, Hiszpanii i Brazylii opisuje się tym samym wykładnikiem, niezależnie od kraju pochodzenia piłkarzy ( 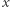to liczba goli, 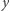- liczba piłkarzy, którzy w ciągu sezonu strzelili 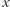bramek). Praca miała w zamierzeniu być spektakularną prezentacją nowego spojrzenia na termodynamikę, w szczególności na pojęcie entropii, które od 1988 roku niestrudzenie lansuje pomysłodawca, Constantino Tsallis.

Internet i komputery - w szczególności dostęp do popularnych stron. Ranking wykazuje, że anglojęzyczne strony Wikipedii są odwiedzane z wykładnikiem ok. 0,3, natomiast w jej polskiej wersji - z wykładnikiem około 0,5 (dane z lipca 2003 r.). Obszerne pakiety programów, np. kompletne systemy operacyjne, składają się z dużej liczby pojedynczych plików. Rozkład ich objętości (tym razem nie ranking!) jest dobrze opisywany prawem potęgowym.

Popularność filmów - zbadano popularność wszystkich filmów wyświetlanych w USA w latach 1997-2003. Zmierzono ją na trzy sposoby: liczba tygodni spędzonych przez nie na liście 60 najbardziej dochodowych projekcji w danym tygodniu, dochód przyniesiony w pierwszym tygodniu wyświetlania oraz łączny czas obecności w kinach. Wszystkie te rozkłady prawdopodobieństwa są słabo skupione, a ich ogony zanikają potęgowo, z wykładnikiem bliskim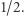

Podatki - okazało się, że ranking cyfr wpisywanych przez podatników w formularze PIT podlega prawu Zipfa, przy czym cyfra "1" ma rangę 1 (w USA). Fakt ten wykorzystano do sporządzenia programu komputerowego, który typuje ewentualnych oszustów podatkowych jedynie na podstawie ich własnych zeznań. Podobno robi to skutecznie, ale bliższych szczegółów nie opublikowano.

Trzęsienia ziemi - histogram przedstawiający logarytm liczby trzęsień ziemi w funkcji ich magnitudy, czyli logarytmu wyzwolonej energii, wykazuje, że jest to zjawisko typu SF. Geolodzy znają je pod nazwą prawa Gutenberga-Richtera (w Japonii jako prawo Omori). Wykładniki, otrzymywane przez różnych badaczy, różnią się w zależności od rejonu, w którym rejestruje się trzęsienia.

Zjawiska atmosferyczne - takie jak np. opady deszczu, zostały zbadane niezwykle starannie w Bostonie przez sieć czujników podłączoną do komputera. Zarówno ilość wody w czasie jednego deszczu (za deszcz uznano opad trwający dłużej niż jedną minutę), jak i odstępy czasu pomiędzy kolejnymi opadami opisują się prawem potęgowym. To samo dotyczy opadów śniegu, ale i monsunów nad wybrzeżem Indii.

Imiona - ranking imion męskich (w USA) ma rozkład potęgowy z wykładnikiem 0,9885, natomiast imion żeńskich 0,9918. Jest to najlepszy przykład prawa Zipfa, tzn. z wykładnikiem najbliższym jedynki, jaki udało się autorowi wyszperać w Internecie.

Szumy 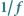- tzn. o amplitudach odwrotnie proporcjonalnych do częstotliwości 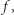od dawna były intrygującą zagadką. Obserwuje się je np. podczas przepływu prądu elektrycznego przez elektrolity. Ich widmo ma w rzeczywistości kształt 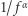z 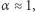ale rozciąga się poprzez kilkanaście dekad częstotliwości: od mikroherców do megaherców.

Kursy giełdowe akcji - w ustalonym dniu. To nie powinno nas zaskakiwać, bo jeśli dochody firm mają rozkład Pareto, to i ceny ich akcji powinny zachowywać się podobnie.

Zachowanie ludzkiego serca - w roku 2001 wykazano, że odstępy pomiędzy okresami małej zmienności aktywności serca pacjenta spełniają prawo Zipfa. Niestety wykładnik jest specyficzny dla każdego z nas oddzielnie i zależy m.in. od naszego trybu życia i nawyków. Proces chorobowy znacząco zmienia wartość wykładnika. Praktyczne zastosowanie tej informacji wymagałoby nieustannego monitoringu naszego cennego organu, na co jednakże nie zanosi się w najbliższej przyszłości.

Cytowania prac naukowych - jeśli ustalimy sobie pewien zbiór prac naukowych, np. wybranego autora, a następnie przeprowadzimy ich ranking, ale tylko tych, które były cytowane przynajmniej raz, to znowu otrzymamy prawo Zipfa-Mandelbrota. Wykładnik okazuje się różny i zależy wyraźnie od wielkości próbki. Na przykład cytowalność 29 prac M. Gell-Manna daje się scharakteryzować wykładnikiem 8,892, natomiast 160 prac E. Wittena - wykładnikiem 2,491. Jeszcze liczniejszy zbiór prac 1120 najczęściej cytowanych fizyków wykazał się wartością wykładnika równą 0,395.

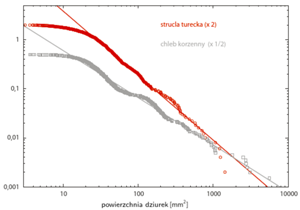
Rys. 1 Rozkład pól dziurek w wyrobach piekarniczych;
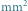są umowne, bo powierzchnie dziurek były mierzone na mocno powiększonych zdjęciach. Dla lepszej czytelności obydwa rozkłady zostały przeskalowane. Wykładniki to: -1,317 (strucla turecka) oraz -0,963 (chleb korzenny)

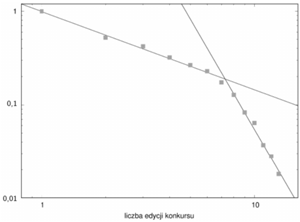
Rys. 2 Prawdopodobieństwo pozostania jurorem/recenzentem w kolejnych edycjach pewnego corocznego konkursu. Widać, że po sześciu latach w składzie jury pozostaje mniej niż 20% jego oryginalnych członków. Wykładniki dla obu gałęzi to -0,836 i -3,925

Podsumujmy. Po pierwsze nie każde zjawisko, którego przejawy mają potęgowy rozkład prawdopodobieństwa, zasługuje na miano zjawiska SF. Kiedy wykładnik potęgi przekracza 3, to rozkład jest na tyle skupiony, że istnieje jego wartość średnia, a wariancja jest skończona. Wykładnik o wartości pomiędzy 2 a 3 zapewnia istnienie jedynie wartości średniej, podczas gdy wariancja staje się nieograniczona - co oznacza, że prognozowanie zjawisk takiego rodzaju musi być bardzo niepewne. Wartość średnią (przeciętną) możemy wówczas mimo wszystko uznać za naturalną jednostkę czy skalę danego zjawiska. Wobec tego na nazwę zjawisk SF zasługują te charakteryzujące się wykładnikiem mniejszym od dwójki, ale większym od jedynki - przynajmniej gdy opisujemy je jako rozkłady prawdopodobieństwa, których "ogony" muszą być całkowalne (żeby całkowita energia szumów 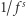była skończona). Ograniczenie 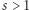nie dotyczy oczywiście sytuacji, kiedy zamiast wielkości fizycznych używamy rang, albo badany rozkład prawdopodobieństwa jest różny od zera jedynie na skończonym odcinku. W szczególności rozkład równomierny można utożsamić z rozkładem potęgowym z wykładnikiem 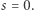Pozostaje jednak problem dla 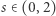w okolicy bliskich zera amplitud badanych zjawisk. Model Mandelbrota, dobry dla obiektów matematycznych zwanych fraktalami, musi się załamać przy opisie rzeczywistości fizycznej. Fraktale to obiekty geometryczne, których fragmenty po powiększeniu wyglądają tak samo jak oryginał (być może obrócony). Proste przykłady to: linia prosta, zbiór Cantora czy dywan Sierpińskiego. Tymczasem "każdy widzi", że powiększania materialnego dywanu Sierpińskiego nie da się prowadzić dowolnie długo. Taki proces musi się zakończyć, kiedy zaczną być widoczne pojedyncze cząsteczki chemiczne. Żartobliwie można powiedzieć, że Przyroda radzi sobie z matematycznymi nieskończonościami na dwa sposoby: od góry - dzięki skończonej prędkości światła i od dołu - poprzez zasadę nieoznaczoności Heisenberga. Bardziej prozaicznie: wielkość dziurek na rysunku 1 jest ograniczona do rozmiarów kromki, z której one pochodzą. Natomiast naturę górnego ograniczenia nośnika rozkładu z rysunku 2 wypada pozostawić Czytelnikowi.