Jak to działa?
Jakie fale nas kręcą?

Fale mogą przenosić pęd i energię. Fala niosąca pęd, oddziałując na obiekt materialny, może mu swój pęd przekazać (czyli zmienić pęd obiektu), a więc będzie działać na niego z pewną siłą (zmiana pędu w czasie to przecież siła). Przykładem takiego zjawiska jest ciśnienie promieniowania elektromagnetycznego - światło pochłaniane przez obiekt materialny wywiera na niego ciśnienie, przekazując mu swój pęd. Efekt ten, choć mierzalny w laboratorium, w życiu codziennym jest praktycznie niezauważalny, ale ciśnienie wywierane na obiekty materialne, na przykład przez fale dźwiękowe, może być naprawdę duże...

Dźwięk silników startującej rakiety potrafi kruszyć szyby w budynkach w odległości kilku kilometrów od niej, a fale, których źródłem są potężne eksplozje, potrafią przewracać budynki. Fale grawitacyjne, które zostały bezpośrednio zaobserwowane w 2015 roku, również przenoszą pęd. Symulacje numeryczne procesu zlewania się dwóch czarnych dziur sugerują, że pęd wynoszony w tym procesie z układu przez promieniowanie może być tak duży, iż powstająca w wyniku zlania się czarna dziura może uzyskać prędkość rzędu kilkuset, a czasami nawet kilku tysięcy km/s względem środka masy układu podwójnego przed połączeniem czarnych dziur. Jej pęd oraz pęd unoszony przez promieniowanie dają w sumie zero w tym układzie, zgodnie z zasadą zachowania pędu. (O zjawisku tym pisaliśmy więcej w Delcie 12/2015).
Skoro fala może przenosić pęd, to nie powinno nikogo dziwić, że może też przenosić moment pędu (w niektórych rejonach Polski nazywany krętem). Skoro fala przekazując materialnemu ciału pęd popycha je, działając z pewną siłą, to przekazując mu moment pędu będzie je rozkręcać, działając momentem siły. Okazuje się, że nie każda fala niesie moment pędu. Powstaje więc naturalne pytanie, jak scharakteryzować te fale, które go przenoszą, i czym one się różnią od tych, które momentu pędu nie niosą, czyli jak wyobrazić sobie fale, które mogą nas rozkręcić.
Jak się za chwilę przekonamy, temat ten jest bardzo ciekawy i bogaty, między innymi dlatego, że istnieją dwa różne mechanizmy odpowiedzialne za przenoszenie momentu pędu przez fale. Mówimy, że fala może mieć spinowy moment pędu związany z polaryzacją lub orbitalny moment pędu związany z kształtem frontu falowego, przy czym fale poprzeczne mogą nieść oba rodzaje, natomiast fale podłużne mogą przenosić tylko orbitalny. Wyjaśnimy sobie teraz wszystkie te pojęcia i związki między nimi w sposób intuicyjny, odwołując się tylko do wyobraźni geometrycznej, bez użycia żadnych wzorów.
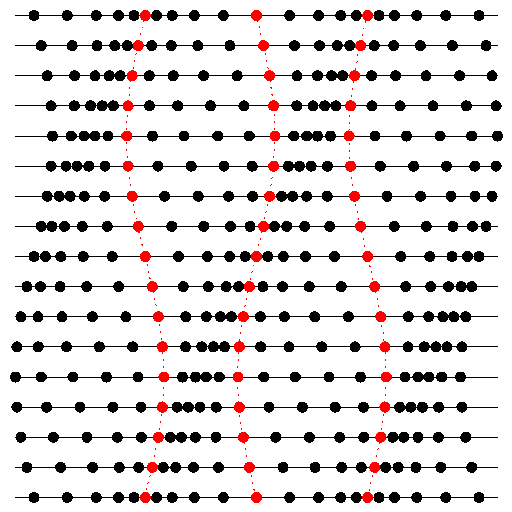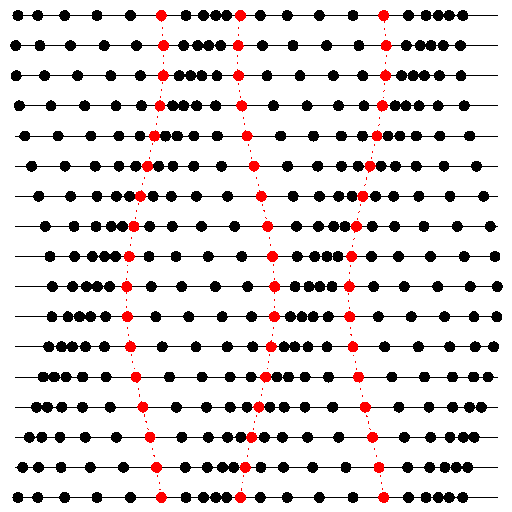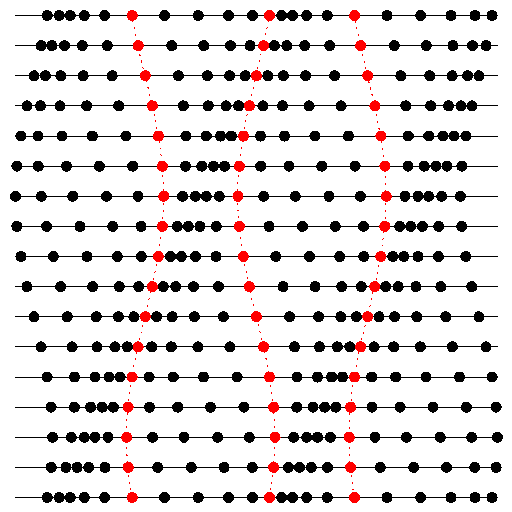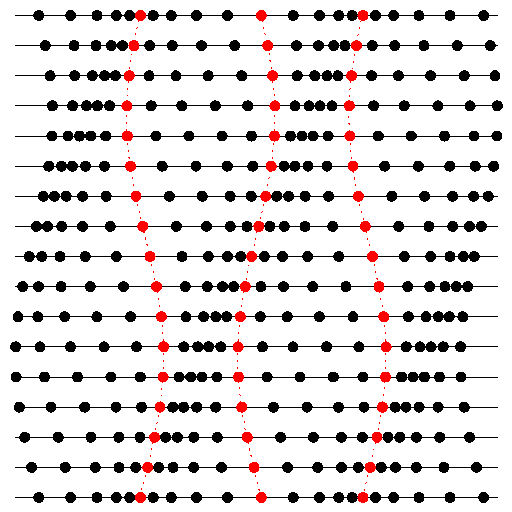
Rys. 1 Schematyczny rysunek fali podłużnej (np. dźwiękowej). Cząsteczki umieszczone na jednej linii wykonują drgania wokół swoich położeń równowagi (trzy cząsteczki zostały wyróżnione kolorem). Kolejne linie reprezentują kolejne chwile. Zakładając, że czas płynie z dołu do góry, widać, jak zagęszczenia i rozrzedzenia przemieszczają się w prawo.
Fala podłużna to taka, dla której drganie ośrodka, w którym się rozchodzi, odbywa się wzdłuż kierunku rozchodzenia się fali. Przykładem takiej fali jest fala dźwiękowa, dla której wielkością, która waha się w czasie, jest ciśnienie. Nasze ucho odbierając dźwięk, rejestruje cykliczne oscylacje ciśnienia wokół wartości średniej, przy czym częstość tych oscylacji odbieramy jako wysokość dźwięku. Gdybyśmy nagle zamrozili powietrze, w którym rozchodzi się fala, albo zrobili jakąś techniką jego zdjęcie, to zobaczylibyśmy zagęszczenia (tam ciśnienie jest większe) i rozrzedzenia (tam ciśnienie jest mniejsze). Cząsteczki powietrza, żeby się zagęszczać i rozrzedzać, muszą się zbliżać i oddalać, przemieszczając się właśnie wzdłuż kierunku rozchodzenia się fali (Rys. 1).

Rys. 2 Polaryzacje liniowe fali elektromagnetycznej. Pole elektryczne (kolor) i magnetyczne (czarne) są prostopadłe. Pole elektryczne górnej fali i dolnej też są prostopadłe. Mówimy, że płaszczyzny polaryzacji tych fal są prostopadłe.
W przypadku fali poprzecznej drganie ośrodka odbywa się w kierunku prostopadłym do kierunku rozchodzenia się fali. Jeżeli szarpniemy napiętą strunę, to zacznie ona drgać wokół położenia równowagi, przy czym zaburzenie, które zapoczątkowaliśmy, będzie rozchodzić się wzdłuż struny. Jest to więc przykład fali poprzecznej, ponieważ wyróżniony punkt na strunie waha się w kierunku prostopadłym do kierunku rozchodzenia się fali. Bardzo ważnym przykładem fali poprzecznej jest fala elektromagnetyczna. Fala taka nie potrzebuje żadnego materialnego ośrodka, żeby się rozchodzić i nawet najprościej jest opisywać jej rozchodzenie się właśnie w próżni. To, co w tym przypadku drga, to natężenie pola elektrycznego i magnetycznego. Okazuje się, że pola te są prostopadłe zarówno do siebie, jak i do do kierunku rozchodzenia się fali. Dodatkowo wartości natężeń tych pól są proporcjonalne, czyli znajomość wektora jednego z nich (np. elektrycznego) wyznacza jednoznacznie wektor tego drugiego (Rys. 2).

Rys. 3 Polaryzacje "  " (po lewej) i "
" (po lewej) i "  " (po prawej) fali grawitacyjnej. Kiedy nie ma fali, cząstki spoczywają na obwodzie okręgu. Kiedy przechodzi fala, cząstki również spoczywają, ale odległości między nimi się zmieniają, co wygląda, jakby cząstki się poruszały tak jak na rysunku.
" (po prawej) fali grawitacyjnej. Kiedy nie ma fali, cząstki spoczywają na obwodzie okręgu. Kiedy przechodzi fala, cząstki również spoczywają, ale odległości między nimi się zmieniają, co wygląda, jakby cząstki się poruszały tak jak na rysunku.
Fala grawitacyjna również jest falą poprzeczną. Żeby taką falę zarejestrować, można mierzyć odległość między dwiema swobodnymi masami próbnymi, spoczywającymi względem siebie w pewnej odległości (np. dwa swobodnie orbitujące satelity). Jeżeli odcinek łączący te masy będzie leżał wzdłuż kierunku rozchodzenia się fali, to żadnego efektu nie zarejestrujemy. Jeżeli będzie w poprzek, to zaobserwujemy, że odległość między masami próbnymi oscyluje. To, co tutaj drga, to czasoprzestrzeń, co manifestuje się właśnie w zmiennej odległości między spoczywającymi względem siebie ciałami. Tradycyjnie ilustruje się to zjawisko wpływem fali grawitacyjnej na masy próbne rozmieszczone na obwodzie okręgu, tak jak na rysunku 3.
Polaryzacja to zjawisko związane z faktem, że dla fali poprzecznej drganie odbywa się w płaszczyźnie prostopadłej do kierunku rozchodzenia się fali, czyli może odbywać się w dowolnym spośród nieskończenie wielu kierunków. Jeżeli odbywa się wzdłuż jednego ustalonego kierunku, to mówimy o polaryzacji liniowej. Można wyróżnić dwa prostopadłe kierunki w płaszczyźnie prostopadłej do kierunku rozchodzenia się fali (Rys. 2) i dowolną polaryzację liniową przedstawiać jako złożenie drgań wzdłuż tych dwóch wyróżnionych kierunków. Dlatego mówi się, że dla fali poprzecznej są dwie możliwe polaryzacje, bo każda inna jest złożeniem tych dwóch.

Rys. 4 Ze złożenia fal elektromagnetycznych o prostopadłych polaryzacjach przesuniętych w fazie o 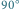 (na górze i na dole) otrzymujemy falę spolaryzowaną kołowo (w środku).
(na górze i na dole) otrzymujemy falę spolaryzowaną kołowo (w środku).
Jednak na polaryzacjach liniowych zabawa się nie kończy. Ze złożenia dwóch prostopadłych drgań o równych amplitudach, ale przesuniętych w fazie o 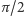 (czyli
(czyli 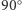 ), uzyskujemy tzw. polaryzację kołową (Rys. 4). Składając drgania o różnych amplitudach, możemy otrzymać każdą z polaryzacji eliptycznych. Dla przykładu, wektor pola elektrycznego dla fali elektromagnetycznej spolaryzowanej liniowo waha się wzdłuż jednego kierunku, a dla fali spolaryzowanej kołowo zatacza okrąg, czyli po prostu się kręci. Ponieważ pole elektryczne pomnożone przez wartość ładunku elektrycznego to siła, jaka działa na ten ładunek, więc pod wpływem fali spolaryzowanej liniowo ładunek wykonuje drgania wzdłuż jednego kierunku, a pod wpływem fali spolaryzowanej kołowo będzie wykonywał ruch po okręgu - fala po prostu go rozkręci.
), uzyskujemy tzw. polaryzację kołową (Rys. 4). Składając drgania o różnych amplitudach, możemy otrzymać każdą z polaryzacji eliptycznych. Dla przykładu, wektor pola elektrycznego dla fali elektromagnetycznej spolaryzowanej liniowo waha się wzdłuż jednego kierunku, a dla fali spolaryzowanej kołowo zatacza okrąg, czyli po prostu się kręci. Ponieważ pole elektryczne pomnożone przez wartość ładunku elektrycznego to siła, jaka działa na ten ładunek, więc pod wpływem fali spolaryzowanej liniowo ładunek wykonuje drgania wzdłuż jednego kierunku, a pod wpływem fali spolaryzowanej kołowo będzie wykonywał ruch po okręgu - fala po prostu go rozkręci.

Rys. 5 Ze złożenia fal grawitacyjnych o polaryzacji "  " (po lewej) i "
" (po lewej) i "  " (po prawej) przesuniętych w fazie o
" (po prawej) przesuniętych w fazie o 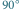 otrzymujemy falę spolaryzowaną kołowo (w środku).
otrzymujemy falę spolaryzowaną kołowo (w środku).
Fala grawitacyjna jako fala poprzeczna ma podobnie jak fala elektromagnetyczna dwie niezależne polaryzacje, schematycznie przedstawione na rysunku 3 Tradycyjnie oznacza się je " 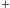 " i "
" i "  ". Dla obu polaryzacji, kiedy odległość między masami próbnymi maleje wzdłuż jednego kierunku prostopadłego do kierunku rozchodzenia się fali, rośnie odległość wzdłuż drugiego kierunku (prostopadłego do pierwszego). Polaryzacje "
". Dla obu polaryzacji, kiedy odległość między masami próbnymi maleje wzdłuż jednego kierunku prostopadłego do kierunku rozchodzenia się fali, rośnie odległość wzdłuż drugiego kierunku (prostopadłego do pierwszego). Polaryzacje " 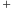 " i "
" i "  " różnią się obrotem o
" różnią się obrotem o 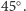 Ze złożenia obu polaryzacji przesuniętych w fazie o
Ze złożenia obu polaryzacji przesuniętych w fazie o 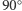 (tak samo jak dla fali elektromagnetycznej) otrzymuje się polaryzację kołową (Rys. 5).
(tak samo jak dla fali elektromagnetycznej) otrzymuje się polaryzację kołową (Rys. 5).
Spinowy moment pędu jest związany z polaryzacją kołową w sposób opisany w poprzednim paragrafie. Jest jasne, że skoro fala elektromagnetyczna spolaryzowana kołowo rozkręca elektron, to przekazuje mu moment pędu. Żeby mu coś przekazać, sama najpierw musi to coś w sobie mieć. Jasne jest również, że skoro spinowy moment pędu jest przenoszony przez fale spolaryzowane kołowo, to fale, których zjawisko polaryzacji nie dotyczy, czyli podłużne, nie mogą tego rodzaju momentu pędu przenosić. Mogą to robić tylko fale poprzeczne, spolaryzowane w szczególny sposób. Fala poprzeczna spolaryzowana liniowo ma zerowy spinowy moment pędu.

Rys. 6 Fala płaska (po lewej) pada na przeszkodę, w której znajduje się mały otwór. Otwór staje się źródłem fali kulistej (po prawej).
Front falowy, zwany inaczej powierzchnią stałej fazy, to powierzchnia, na której wszystkie punkty ośrodka, w jakim rozchodzi się fala o pewnej ustalonej częstości, są w jednej chwili w tej samej fazie ruchu drgającego. Może to być, na przykład, chwila maksymalnego wychylenia z położenia równowagi albo chwila przejścia przez stan równowagi. Dla ustalenia uwagi skupmy się na powierzchniach złożonych z punktów, w których akurat następuje przejście przez stan równowagi (wychylenie jest równe zeru). Od kształtu tych powierzchni biorą się takie nazwy jak fala płaska, czyli taka, dla której front falowy jest płaszczyzną, czy fala kulista, dla której front falowy jest sferą (może trafniej byłoby nazywać je falami sferycznymi?). Te dwa wymienione przykłady są szczególnie ważne, ponieważ fale kuliste rozchodzą się z punktowego źródła, natomiast fale płaskie są dobrym przybliżeniem wtedy, gdy rozpatrujemy falę w małej objętości znajdującej się w dużej odległości od źródła (Rys. 6). Gdy popatrzymy, jak zmienia się front falowy w czasie, to zobaczymy, że po prostu przesuwa się w kierunku rozchodzenia się fali (w szczególności dla fali płaskiej płaszczyzny przesuwają się wzdłuż kierunku do nich prostopadłego, a dla fali kulistej sfery puchną).

Rys. 7 Kształt frontu falowego fali niosącej orbitalny moment pędu.
Orbitalny moment pędu jest związany z własnościami frontu falowego - po prostu front falowy musi się w pewnym sensie kręcić. Ani fale płaskie, ani kuliste nie mogą nieść orbitalnego momentu pędu, ponieważ nic tam się nie kręci, a ściślej, nie widać, żeby się kręciło, ponieważ zarówno płaszczyzna, jak i sfera, obracając się, ślizgają się po sobie. Nie da się wiec odróżnić frontu falowego w kształcie sfery obracającej się od sfery nieobracającej się. Typowy kształt frontu falowego niosącego orbitalny moment pędu przedstawia rysunek 7 Ma on charakterystyczny helikoidalny kształt. Powierzchnia ta jest nawinięta wokół pewnej osi (tzw. osi wirowej), na której amplituda fali znika. Oś wirowa leży wzdłuż kierunku rozchodzenia się fali i kiedy front falowy przesuwa się wzdłuż tego kierunku, to jego ruch wygląda jak obrót tej powierzchni wokół osi wirowej (śruba, która się obraca i śruba, która się przesuwa, wyglądają tak samo). Oba rodzaje fal (podłużne i poprzeczne) mogą przenosić orbitalny moment pędu, ponieważ nie ma on związku z polaryzacją. Wiązki fal, niosące orbitalny moment pędu, mogą mieć różną naturę (dźwiękowe, elektromagnetyczne, grawitacyjne) i bardzo różne własności, ale to, co je wyróżnia, to właśnie charakterystyczny kształt frontu falowego, który zawsze jest podobny do tego z rysunku 7.
Z tego, co zostało powyżej przedstawione, widać już, że temat momentu pędu fali jest bardzo bogaty, a to dopiero wierzchołek góry lodowej. Wiemy, na przykład, że fala płaska albo kulista nie niesie orbitalnego momentu pędu, ale jeżeli jest falą poprzeczną (która może mieć różne polaryzacje) to może nieść spinowy moment pędu. W ogólności wiązki fal poprzecznych mogą być nośnikiem obu typów momentu pędu i dla skomplikowanych wiązek problem rozdzielenia całkowitego momentu pędu niesionego przez falę na składowe spinową i orbitalną jest trudny i czasem może nie mieć jednoznacznego rozwiązania. Okazuje się również, że wiązki fal, niosące moment pędu, mają dużo więcej ciekawych własności, niż to, że potrafią rozkręcać cząstki z nimi oddziałujące. Więcej o własnościach i zastosowaniach fal niosących moment pędu napiszemy w następnym numerze Delty.
 " (po lewej) i "
" (po lewej) i "  " (po prawej) fali grawitacyjnej. Kiedy nie ma fali, cząstki spoczywają na obwodzie okręgu. Kiedy przechodzi fala, cząstki również spoczywają, ale odległości między nimi się zmieniają, co wygląda, jakby cząstki się poruszały tak jak na rysunku.
" (po prawej) fali grawitacyjnej. Kiedy nie ma fali, cząstki spoczywają na obwodzie okręgu. Kiedy przechodzi fala, cząstki również spoczywają, ale odległości między nimi się zmieniają, co wygląda, jakby cząstki się poruszały tak jak na rysunku.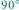 (na górze i na dole) otrzymujemy falę spolaryzowaną kołowo (w środku).
(na górze i na dole) otrzymujemy falę spolaryzowaną kołowo (w środku). " (po lewej) i "
" (po lewej) i "  " (po prawej) przesuniętych w fazie o
" (po prawej) przesuniętych w fazie o 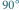 otrzymujemy falę spolaryzowaną kołowo (w środku).
otrzymujemy falę spolaryzowaną kołowo (w środku).