Jak to działa?
Nowe pomysły
Superkomputery
Fizyka a obliczenia równoległe

Komputery, największy wynalazek nowożytności, mają coraz więcej zastosowań. Jedne pracują w telefonach komórkowych i urządzeniach przenośnych. Innym - superkomputerom - zlecamy np. symulację historii wszechświata. Może kiedyś nauczymy je myśleć podobnie do tego jak sami myślimy. We wstępnym artykule z serii o współczesnych kierunkach w technikach obliczeniowych (zwłaszcza superkomputerowych) pokażemy, jak fizyka tranzystora umożliwiła technologii mikroprocesorowej podwoić prędkość komputerów więcej niż dwadzieścia kolejnych razy (tj. o czynnik 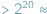 milion razy), umożliwiając szybki internet, smartfony i współczesną naukę obliczeniową, i dlaczego kontynuacja dotychczasowego wykładniczego rozwoju techniki komputerowej od trzynastu lat wymaga od programistów zasadniczo nowego podejścia: programowania współbieżnego procesorów wielordzeniowych.
milion razy), umożliwiając szybki internet, smartfony i współczesną naukę obliczeniową, i dlaczego kontynuacja dotychczasowego wykładniczego rozwoju techniki komputerowej od trzynastu lat wymaga od programistów zasadniczo nowego podejścia: programowania współbieżnego procesorów wielordzeniowych.
Komputery są niezbędne do coraz szerszej listy zastosowań, od użytkowych (komunikatory osobiste, media i handel internetowy) i rozrywkowych (zaawansowane gry) do naukowych i inżynieryjnych, czyli od wymiany i analizy wartko rosnącego strumienia informacji, do symulacji rzeczywistości i prób prawdziwie inteligentnego przetwarzania informacji. Gdy wybiegniemy nieco w przyszłość, ale sądząc z rosnącego tempa rozwoju inteligencji maszynowej, w szczególności uczenia maszynowego - w całkiem niedaleką już przyszłość, nasze życie i światowy rynek pracy będą zmieniać się szybko dzięki tej jakościowo nowej fali komputeryzacji w stopniu nie mniejszym od tego, jak mechanizacja produkcji zmieniła społeczeństwa w epoce rewolucji przemysłowej. Niekoniecznie musi to oznaczać dominację maszyn i bezrobocie ludzi. Na przykład to, że pojazdy mechaniczne wyeliminowały konie i woźniców, nie oznaczało bynajmniej spadku zatrudnienia w transporcie. Pojawił się zawód kierowcy. Niedługo znajdzie się on na liście zawodów zagrożonych. Kierowców zastąpią komputery z wielkimi bazami danych, łącznością satelitarną, widzeniem i adaptacyjnym uczeniem maszynowym. W przewidywalnej przyszłości naukowcy czy lekarze i - niestety - również niektórzy politycy nie pójdą w ślady zapalaczy lamp gazowych (popularna w XIX wieku profesja).
Odpowiednikiem maszyny parowej, motoru rewolucji przemysłowej, jest dziś procesor komputera. Obliczenia równoległe jednego zadania na procesorach wielordzeniowych (tj. na wielu kalkulatorach naraz) mają zaś historyczny odpowiednik w metodzie produkcji masowej rozwiniętej w fabryce samochodów Forda w 1913 roku - zwiększają znacznie tempo obliczeń. Analogia jest o tyle niepełna, że każdy pracownik na taśmie produkcyjnej Forda mógł być (z założenia) mało wykształcony, w odróżnieniu od rzemieślnika tworzącego cały produkt samemu. Dzisiaj natomiast, jak zobaczymy, zachodzi konieczność przestawienia się programisty z myślenia i programowania sekwencyjnego na tworzenie programów współbieżnych albo równoległych (jak jednoczesna produkcja samochodów na równoległych taśmach produkcyjnych). A to wymaga nie mniejszych, lecz większych umiejętności niż programowanie zwykłego komputera von Neumanna, który pobiera i wykonuje jedną po drugiej instrukcje przy użyciu jednego kalkulatora (rdzenia obliczeniowego).
Postęp geometryczny
W latach 60. ubiegłego wieku współzałożyciel firmy Intel, Gordon Moore, sformułował empiryczną regułę geometrycznego postępu szybkości komputerów w ich kolejnych, regularnie co dwa lata (lub nawet nieco częściej) powstających pokoleniach procesorów komputerowych. Ściślej, prawo Moore'a mówi, że liczba tranzystorów na jednostkę powierzchni, tj. gęstość upakowania tranzystorów w płaskim układzie scalonym podwaja się co około dwa lata. Prawo jest szeroko znane, gdyż faktycznie tak zmieniała się ta liczba przez niesłychanie wiele pokoleń technologii procesorowych: ponad 20 (czyli przez ostatnie 40 lat) i ponieważ taki wykładniczy przyrost liczby bramek logicznych i komórek pamięci lokalnej w procesorze leży u podstaw błyskotliwej kariery komputera, a w miarę jak komputery stają się niezbędne, postępu technicznego cywilizacji. Spójrzmy na liczby opisujące typowy zaawansowany procesor główny (CPU, od ang. Central Processor Unit) w roku 1975 i 2015. Szybkość działania CPU mierzona jest liczbą najprostszych działań arytmetycznych zmiennoprzecinkowych na sekundę (jednostka zapisywana jako FLOP albo FLOP/s, to właśnie oznacza: floating point operation per second). Wynosiła w roku 1975 około 0,1 MFLOP (0,1 miliona FLOP). Czterdzieści lat później procesor CPU był już milion razy szybszy, 0,1-0,3 TFLOP (teraflop to 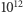 działań/s), a koprocesory obliczeniowe osiągnęły 1 TFLOP w podwójnej precyzji obliczeń. Liczba tranzystorów w procesorach dochodzi do około 10 miliardów.
działań/s), a koprocesory obliczeniowe osiągnęły 1 TFLOP w podwójnej precyzji obliczeń. Liczba tranzystorów w procesorach dochodzi do około 10 miliardów.

Rys. 1 Fragment procesora Apple A7, gdzie dziesięć tranzystorów ułożonych jest na odcinku 1138 nm. Procesor ten, znajdujący się w telefonach iPhone 5S, oparty jest na połączeniach o grubości 28 nm, tj. rzędu 70 odległości między atomami krzemu. (W latach 2010-2014 szerokość ścieżki procesorów Intel Corp. zmalała z 32 i 28 nm do 22 nm, a następnie do 14 nm). Szybko rosnący koszt produkcji tych niezawodnych, mikroskopijnych układów musi się producentom zwrócić. To zmusza ich do nieco rzadszej niż dawniej zmiany technologii produkcji. Pesymiści ogłosili wręcz, że pokolenie procesorów w technologii 10 nm będzie już ostatnim opłacalnym, czyli końcem technologii krzemowej. To niekoniecznie prawda. W odwodzie są też nowe substraty, np. grafen, prawdziwie 2-wymiarowa, heksagonalna sieć atomów węgla, która może kiedyś zastąpi krzem. Istnieje poważny, atomowo-kwantowy limit miniaturyzacji, związany z odległościami między atomami krzemu równymi 0,43 nm. Standardowy tranzystor nie będzie działał klasycznie po miniaturyzacji do kilku nanometrów i schemat funkcjonowania komputera musi być wtedy wymyślony od podstaw.
Prawo Moore'a nie było przypadkiem. Przeciwnie, było decyzją przemysłu elektronicznego, umożliwioną szczęśliwie przez prawa fizyki. Projektanci procesorów (np. Intel) miniaturyzowali podzespoły tak, by następna generacja procesora na tej samej powierzchni mieściła dwa razy więcej tranzystorów. To prawo Moore'a. Ale gdyby krok miniaturyzacji wymuszał np. dwa razy większe straty cieplne, to taka miniaturyzacja musiałaby być zatrzymana po kilku etapach miniaturyzacji. Kontynuowana, doprowadziłaby do tego, że obecnie komputer domowy zużywałby megawaty mocy, a telefon komórkowy rozładowywałby baterię w ułamku sekundy. Sprawdźmy zatem konsekwencje skalowania rozmiaru dla mocy pobieranej przez procesor, zamienianej na ciepło wskutek zjawiska oporności elektrycznej. Odprowadzenie znacznej ilości ciepła jest w istocie większym wyzwaniem, niż dostarczenie energii elektrycznej, choć koszty energii są niebagatelne. W przypadku superkomputerów są porównywalne z kosztem ich zakupu.
Bariera energii
Pierwsze mikroprocesory mało się grzały. Za to teraz zderzyliśmy się we wszystkich rodzajach obliczeń, od telefonii do centrum obliczeniowego, z barierą energetyczną. Pojedyncze procesory (CPU, koprocesory arytmetyczne i karty graficzne) nie mogą pobierać więcej niż 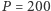 W, a najwyżej 300 W, inaczej byłoby trudno je zasilać w budynku mieszkalnym i równie trudno byłoby wentylować pokoje komputerowe. Na limit mocy napotykają też procesory w telefonach komórkowych i tabletach: długość pracy urządzenia bez ładowania baterii jest odwrotnie proporcjonalna do
W, a najwyżej 300 W, inaczej byłoby trudno je zasilać w budynku mieszkalnym i równie trudno byłoby wentylować pokoje komputerowe. Na limit mocy napotykają też procesory w telefonach komórkowych i tabletach: długość pracy urządzenia bez ładowania baterii jest odwrotnie proporcjonalna do 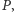 co nakłada na moc górne ograniczenie.
co nakłada na moc górne ograniczenie.
Energia elektryczna potrzebna do obliczeń szybko rośnie z częstotliwością 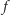 zegara procesora, jak i liczbą
zegara procesora, jak i liczbą 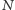 tranzystorów. Bramka logiczna ma jeden lub więcej tranzystorów o efektywnej pojemności elektrycznej
tranzystorów. Bramka logiczna ma jeden lub więcej tranzystorów o efektywnej pojemności elektrycznej 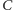 (jest to stosunek ładunku do potencjału elektrycznego,
(jest to stosunek ładunku do potencjału elektrycznego, 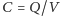 ). Ma także pewną oporność. Zmiana stanu bramki wymaga naładowania pojemności
). Ma także pewną oporność. Zmiana stanu bramki wymaga naładowania pojemności 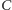 poprzez opornik od potencjału zerowego do napięcia operacyjnego
poprzez opornik od potencjału zerowego do napięcia operacyjnego 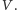 Przepływając przez źródło napięcia
Przepływając przez źródło napięcia 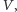 ładunek
ładunek 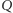 uzyskuje energię
uzyskuje energię 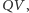 czyli
czyli 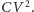 Sumowanie przyczynków do elektrostatycznej energii potencjalnej tranzystora pokazuje, że niezależnie od wartości oporności bramki połowa energii źródła gromadzona jest na tranzystorze, a połowa zamieniana w czasie ładowania na ciepło. Tylko nieliczne procesory potrafią odzyskać tę pierwszą energię potencjalną, większość w końcu traci całość dostarczonej energii
Sumowanie przyczynków do elektrostatycznej energii potencjalnej tranzystora pokazuje, że niezależnie od wartości oporności bramki połowa energii źródła gromadzona jest na tranzystorze, a połowa zamieniana w czasie ładowania na ciepło. Tylko nieliczne procesory potrafią odzyskać tę pierwszą energię potencjalną, większość w końcu traci całość dostarczonej energii 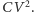 Maksymalna moc rozpraszana w czasie obliczeń prowadzonych
Maksymalna moc rozpraszana w czasie obliczeń prowadzonych 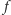 razy na sekundę na
razy na sekundę na 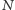 bramkach logicznych procesora zależy więc od
bramkach logicznych procesora zależy więc od 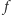 i
i 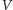 :
:

Jak zmieniają się parametry tranzystora przy zmianie generacji, tj. zmniejszeniu jego struktury o czynnik liniowy 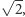 a pola powierzchni o czynnik
a pola powierzchni o czynnik 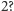 Spójrzmy na kolejne czynniki powyższego wyrażenia na moc
Spójrzmy na kolejne czynniki powyższego wyrażenia na moc 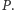 Liczba tranzystorów
Liczba tranzystorów 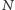 podwaja się. Pojemność
podwaja się. Pojemność 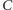 to pewna stała materiałowa razy pole powierzchni elektrod (np. okładek kondensatora), podzielone przez odległość między nimi (to wynika z praw Coulomba i Gaussa w elektrostatyce). Ponieważ pole powierzchni spada dwukrotnie, a wszystkie odległości o czynnik skalowania
to pewna stała materiałowa razy pole powierzchni elektrod (np. okładek kondensatora), podzielone przez odległość między nimi (to wynika z praw Coulomba i Gaussa w elektrostatyce). Ponieważ pole powierzchni spada dwukrotnie, a wszystkie odległości o czynnik skalowania 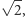 to pojemność
to pojemność 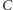 bramki spada o czynnik
bramki spada o czynnik 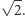 Inżynierowie przy zmniejszeniu rozmiarów tranzystorów zmniejszali też o czynnik
Inżynierowie przy zmniejszeniu rozmiarów tranzystorów zmniejszali też o czynnik 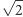 różnicę potencjału
różnicę potencjału 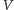 tak, by pole elektryczne (tzn. potencjał podzielony przez odległość elektrod) pozostało stałe. Przy niezmienionym
tak, by pole elektryczne (tzn. potencjał podzielony przez odległość elektrod) pozostało stałe. Przy niezmienionym 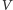 pole elektryczne za bardzo by w końcu wzrosło, niszcząc właściwości półprzewodnika. Zmiany stanu półprzewodników w tranzystorze zajmują pewien czas, który jest tym większy, im grubsze są warstwy półprzewodnika. I odwrotnie - zmniejszenie grubości pozwalało na zmniejszenie czasu przeładowania tranzystora. Dlatego częstotliwość
pole elektryczne za bardzo by w końcu wzrosło, niszcząc właściwości półprzewodnika. Zmiany stanu półprzewodników w tranzystorze zajmują pewien czas, który jest tym większy, im grubsze są warstwy półprzewodnika. I odwrotnie - zmniejszenie grubości pozwalało na zmniejszenie czasu przeładowania tranzystora. Dlatego częstotliwość 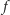 była zwiększana przy miniaturyzacji
była zwiększana przy miniaturyzacji 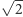 razy. Zmiany wielkości po prawej stronie wyrażenia na
razy. Zmiany wielkości po prawej stronie wyrażenia na 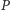 zebrane w jedną liczbę dają stałą wartość równą
zebrane w jedną liczbę dają stałą wartość równą

I tu właśnie leży tajemnica trzydziestoletniego sukcesu procedury skalowania: nie wymagało ono dostarczenia większej mocy tranzystorom na centymetrze kwadratowym powierzchni. Pobór mocy procesora rósł z innego powodu, takiego, że pole jego powierzchni w umiarkowanym tempie zwiększano. Liczba tranzystorów powiększała się o więcej niż czynnik 2. Można było użyć tak liczne tranzystory do zwiększania złożoności logiki procesora oraz na wewnętrzną, szybką pamięć zwaną podręczną (ang. cache). Było to potrzebne do maskowania narastającej od 2000 r. powolności pamięci operacyjnej RAM (Random Access Memory) w stosunku do CPU. Zastosowano coraz bardziej skomplikowane kolejki danych i instrukcji ściąganych przedwcześnie do pamięci podręcznej. Dzięki takim metodom szybkość zegara pomiędzy generacjami procesorów rosła nie o czynnik 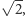 lecz około dwukrotnie. Tempo rozwoju techniki obliczeniowej było fenomenalne.
lecz około dwukrotnie. Tempo rozwoju techniki obliczeniowej było fenomenalne.
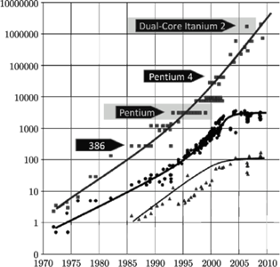
Rys. 2 Wzrost w kolejnych latach liczby tranzystorów 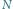 w tysiącach (
w tysiącach (  ), częstotliwości zegara procesora
), częstotliwości zegara procesora 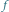 w megahercach
w megahercach 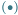 i mocy elektrycznej jego zasilania
i mocy elektrycznej jego zasilania  w watach
w watach 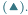
Idylla skalowania zakończyła się w latach 2003-2004, kiedy inne niż oporność elektryczna zjawisko dorównało dyssypacji energii w tranzystorze. Jest to prąd ucieczki (ang. leakage current), przeciekanie elektronów przez nominalnie nieprzewodzącą warstwę półprzewodnika. Zjawisko było drugorzędne przy dużych początkowo wartościach 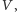 ale po kolejnym zmniejszeniu
ale po kolejnym zmniejszeniu 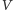 dyssypacja energii związana z prądem ucieczki zaczęła dominować. Wynik był natychmiastowy, choć nienagłaśniany. Od tej pory utrzymywano
dyssypacja energii związana z prądem ucieczki zaczęła dominować. Wynik był natychmiastowy, choć nienagłaśniany. Od tej pory utrzymywano 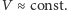 Aby wydzielana moc cieplna
Aby wydzielana moc cieplna 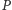 nie przekroczyła bariery energetycznej, konieczne też było praktyczne zamrożenie szybkiego uprzednio przyrostu częstotliwości
nie przekroczyła bariery energetycznej, konieczne też było praktyczne zamrożenie szybkiego uprzednio przyrostu częstotliwości 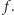 Ilustruje to rysunek 2 pokazujący historię zmian
Ilustruje to rysunek 2 pokazujący historię zmian 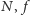 i
i 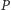 w latach 1970-2010. Po roku 2004 szybki przyrost
w latach 1970-2010. Po roku 2004 szybki przyrost 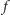 zakończył się. Dla oszczędności energii redukowano w niektórych urządzeniach
zakończył się. Dla oszczędności energii redukowano w niektórych urządzeniach 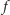 poniżej wartości 2-4 GHz osiąganych wcześniej. Tak jest np. w nowych procesorach arytmetycznych Intel Xeon Phi oraz procesorach graficznych (GPU), które mają obecnie
poniżej wartości 2-4 GHz osiąganych wcześniej. Tak jest np. w nowych procesorach arytmetycznych Intel Xeon Phi oraz procesorach graficznych (GPU), które mają obecnie 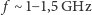 . W cieniu bariery energetycznej wymuszającej
. W cieniu bariery energetycznej wymuszającej 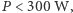
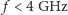 oraz
oraz 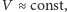 prędkość obliczeń dość trudno jest dalej podnosić. Jest to absolutnie niemożliwe, jeśli zachowamy dawną architekturę procesora z tylko jednym, szybkim, centralnym kalkulatorem.
prędkość obliczeń dość trudno jest dalej podnosić. Jest to absolutnie niemożliwe, jeśli zachowamy dawną architekturę procesora z tylko jednym, szybkim, centralnym kalkulatorem.

Myśleć równolegle
Świat (techniki obliczeniowej) uratowała po roku 2004 wielordzeniowość procesorów. To, że sprzedaje się teraz w sklepach procesory o coraz większej liczbie niezależnych rdzeni 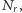 przyspiesza komputer proporcjonalnie do
przyspiesza komputer proporcjonalnie do 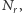 ale tylko pod warunkiem odpowiedniego dostosowania algorytmów. Gdyby nie działała nieubłagana fizyka, w tej chwili moglibyśmy liczyć na jednym rdzeniu CPU o
ale tylko pod warunkiem odpowiedniego dostosowania algorytmów. Gdyby nie działała nieubłagana fizyka, w tej chwili moglibyśmy liczyć na jednym rdzeniu CPU o 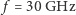 , zamiast na 10 rdzeniach CPU o
, zamiast na 10 rdzeniach CPU o 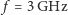 albo na 60 rdzeniach procesora Xeon Phi o zegarze 1,1 GHz. Programowanie byłoby tradycyjne, łatwiejsze, i wszystkie rodzaje zadań wykonywałyby się szybko. Ale w realnym świecie nie moglibyśmy tego robić w budynku mieszkalnym, gdzie nadmierny pobór prądu aktywowałby bezpieczniki!
albo na 60 rdzeniach procesora Xeon Phi o zegarze 1,1 GHz. Programowanie byłoby tradycyjne, łatwiejsze, i wszystkie rodzaje zadań wykonywałyby się szybko. Ale w realnym świecie nie moglibyśmy tego robić w budynku mieszkalnym, gdzie nadmierny pobór prądu aktywowałby bezpieczniki!
Obecna ewolucja procesora polega na powielaniu w mniejszej skali przestrzennej rdzenia obliczeniowego o ograniczonej liczbie tranzystorów tak, aby obliczenia szły coraz większą liczbą równoległych torów (wątków programu). To pozwoliło procesorom kontynuować bicie rekordów sumarycznej mocy obliczeniowej (to temat następnego artykułu z tej serii). Ułatwiło procesorom, ale nie wszystkim programistom, i nie we wszystkich zastosowaniach. Rewolucja wielowątkowości została programistom narzucona przez inżynierów, ale - jak widzieliśmy - był bardzo istotny powód: energetyka tranzystora. Niektórzy opierają się do dziś idei programowania kart graficznych do celów obliczeniowych, mimo że do niektórych zastosowań w tej dekadzie będą to urządzenia zdecydowanie najszybsze (m.in. do uczenia maszynowego). Dla nich najlepszym rozwiązaniem mogą być procesory MIC (Many Integrated Cores), czyli Liczne Zintegrowane Rdzenie, jak Xeon Phi firmy Intel. Uruchamianie na nich programu, zwłaszcza wcześniej działającego programu sekwencyjnego, trwa krócej niż w przypadku GPU, urządzenia o podobnej liczbie 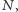 ale odmiennej architekturze i hierarchii pamięci. W obu przypadkach nietrywialne programowanie nowoczesnych maszyn obliczeniowych jest jednak ciekawe, gdyż ich moce obliczeniowe nadal bardzo szybko rosną i pozwalają atakować dotychczas nierozwiązywalne problemy. Celem wytyczonym przez ministerstwo energii USA jest budowa do 2020 roku komputera robiącego
ale odmiennej architekturze i hierarchii pamięci. W obu przypadkach nietrywialne programowanie nowoczesnych maszyn obliczeniowych jest jednak ciekawe, gdyż ich moce obliczeniowe nadal bardzo szybko rosną i pozwalają atakować dotychczas nierozwiązywalne problemy. Celem wytyczonym przez ministerstwo energii USA jest budowa do 2020 roku komputera robiącego 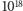 działań arytmetycznych na sekundę (exaflop). Można też zbudować mini-superkomputer u siebie w domu i prowadzić obliczenia, np. dynamiki gazu, o czym opowie trzeci odcinek z tej serii.
działań arytmetycznych na sekundę (exaflop). Można też zbudować mini-superkomputer u siebie w domu i prowadzić obliczenia, np. dynamiki gazu, o czym opowie trzeci odcinek z tej serii.


A co dalej? Komputer kwantowy
Przewodniki w najnowszych CPU mają grubość 14 nm albo 40 warstw atomowych krzemu. Zmniejszenie ich 10 razy spowoduje, że procesor zacznie zachowywać się dziwnie, nieprzewidywalnie, gdyż elektrony i atomy będą przejawiały cechy kwantowe. Koncepcję obliczeń kwantowych sformułował fizyk, Richard Feynman, w 1981 roku. W wielu laboratoriach na świecie już teraz fizycy i inżynierowie dokonali w praktyce przeskoku do warstw jednoatomowych i koniecznego przy tym przejścia do fizyki kwantowej. Oczekujemy, że za około dziesięć lat zbudowane zostaną pierwsze użytkowe egzemplarze komputerów kwantowych. Cząstki reprezentować mogą jednocześnie wartości logiczne zera i jedynki na zasadzie superpozycji stanów kwantowych (w takim podwójnym stanie jest kot w słynnym eksperymencie myślowym Schrödingera). Jest więc pewne, że można będzie niesłychanie szybko sprawdzać wyniki wszystkich możliwych kombinacji zer i jedynek w obliczeniu probabilistycznym bądź kryptologicznym, jak i w niektórych problemach optymalizacji. Problem rozkładu dużej liczby naturalnej na czynniki pierwsze (ważny przy deszyfracji kodów) został kwantowo-algorytmicznie rozwiązany 23 lata temu. Nie jest tylko jasne, do ilu problemów spoza kombinatoryki i probabilistyki komputer kwantowy będzie się nadawał, czy będzie miał funkcjonalność komputera von Neumanna. Jeśli tak, to czeka nas zmiana paradygmatu obliczeń. Entuzjastyczne badania trwają, ale przez najbliższe 25 lat nie pozbywałbym się jeszcze komputera klasycznego.
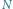 w tysiącach (
w tysiącach (  ), częstotliwości zegara procesora
), częstotliwości zegara procesora 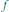 w megahercach
w megahercach 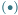 i mocy elektrycznej jego zasilania
i mocy elektrycznej jego zasilania  w watach
w watach