Aby na te pytania odpowiedzieć, rozpatrzmy najpierw kilka przykładów.

• Jedną z podstawowych czynności fizyka jest pomiar. Mierząc cokolwiek, używa on określonych jednostek. Na pierwszy rzut oka oceniamy, że jest rzeczą obojętną, jak będą jednostki te wybrane. Jednakże, poniekąd wbrew temu oczekiwaniu, nie mierzymy czasu np. w uderzeniach serca lub zdrowaśkach, ani też odległości np. w stopach czy też łokciach, lecz, odpowiednio, w sekundach i metrach oraz w jednostkach pochodnych. Co więcej, z definicjami tych jednostek też dzieją się jakieś dziwne rzeczy. Metr na przykład odnoszono początkowo do obwodu Ziemi, potem wykonano wzorzec "ze stopu platyno-irydowego", a teraz jednostkę tę wiąże się z długością fali światła, odpowiadającej określonemu rodzajowi promieniowania określonego rodzaju atomów. Dlaczego?
• "Wiadomo", że ciała przyciągają się siłą grawitacyjną odwrotnie proporcjonalną do drugiej potęgi ich wzajemnej odległości. Jest jednak rzeczą jasną, że wyniki eksperymentalne moglibyśmy w granicach błędu odtworzyć, zakładając, iż potęga ta nie jest równa dokładnie 2, lecz 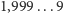z dostatecznie dużą liczbą dziewiątek. Tymczasem w podręcznikach figuruje zawsze 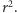Dlaczego?
• Jak głosi znana anegdota, która w dodatku jest najprawdopodobniej prawdziwa, Newton powziął swoją ideę prawa powszechnego ciążenia pod wpływem widoku spadającego jabłka. Kolejny krok jego rozumowania polegał na zadaniu sobie pytania, czy ciało umieszczone tak daleko od Ziemi, jak Księżyc, także by na nią spadło. Co za pomysł! Biorąc pod uwagę, że jabłko tylko w niewielkim stopniu przypomina Księżyc, nie widać powodu, aby ruchem (i to tak odmiennym!) obu tych ciał rządziło to samo prawo. Jabłko np. składa się z substancji organicznych: czemu nie miałyby tu działać jakieś "siły witalne"?
• Teoria Newtona dostarcza nam oszałamiająco pięknego wyjaśnienia ruchów planet. Jednakże w początku XIX wieku stało się jasne, że ruch najdalszej ze znanych wówczas planet, Urana, nie spełnia ściśle przewidywań wynikających z teorii Newtona. Oczywiście można by odrzucić tę teorię. Le Verrier i Adams zaryzykowali jednak inną hipotezę, zakładając, że poza Uranem krąży wokół Słońca jeszcze jedna planeta, której wpływ na ruch Urana wyjaśniałby odstępstwa od teorii Newtona. I rzeczywiście, w roku 1846 Galle wykrył tę planetę (Neptuna). Podobne rozważania doprowadziły do wykrycia kolejnej planety, tj. Plutona (1930). Warto jednak wiedzieć, że także ruch Merkurego nie stosuje się ściśle do przewidywań teorii Newtona. I tym razem Le Verrier w roku 1859 spróbował tego samego wyjaśnienia, postulując istnienie planety jeszcze bliższej Słońcu niż Merkury (Wulkana). Planeta ta, co więcej, pod wpływem potężnych, jak widać, sił psychologicznych aż dwukrotnie została odkryta (1859, 1876); jak wiadomo, były to doniesienia błędne. Zaproponowano więc jeszcze inną hipotezę, w której niczego nie trzeba by już odkrywać, a mianowicie, że między Merkurym a Słońcem znajduje się smuga rozrzedzonej materii, która tłumaczyłaby odstępstwa ruchu Merkurego od przewidywań newtonowskich. Hipoteza ta jednak nie została zaakceptowana. Dlaczego? Poprawne rozwiązanie problemu Merkurego daje ogólna teoria względności. Dlaczego właśnie ta teoria znalazła uznanie wśród fizyków?
• Przyspieszenie jest pochodną prędkości względem czasu. Pochodne, jak wiadomo, można obliczać tylko w tym obszarze argumentów, w którym funkcja różniczkowana jest ciągła. Znaczy to, że zakładamy, mniej lub bardziej milcząco, że prędkość jest funkcją ciągłą czasu. Na jakiej podstawie czynimy to założenie?

Wprawdzie tylko ostatni punkt nawiązuje wprost do tytułu niniejszego artykułu, jednakże warto przynajmniej przez chwilę rozpatrywać wszystkie punkty łącznie, gdyż rzucają one wspólnie światło na to, co w fizyce, a ogólniej w nauce, jest w gruncie rzeczy pozanaukowe.

Wróćmy do przykładu z jednostkami miary. Oczywiście każdy badacz mógłby wyrażać wyniki swoich pomiarów w dowolnych jednostkach, na przykład długość we własnych stopach. Gdyby jednak tak było, uzyskane przez niego wyniki nie mogłyby być sprawdzane przez innych badaczy. Co więcej, jednostki należące do układu takiego jak np. cal (grubość kciuka), stopa, łokieć, mila itd. pozostają w skomplikowanych stosunkach arytmetycznych, co utrudnia efektywne posługiwanie się nimi. Jest chyba oczywiste, że dziesiętny układ metryczny najlepiej służy sprawie kilku zasad przyjmowanych w fizyce, do których należy zaliczyć intersubiektywność wyników oraz wygodę w posługiwaniu się aparatem rachunkowym.

Przykład z prawem Newtona (równie dobrze można by tu mówić o prawie Coulomba) świadczy, że w fizyce przyjmuje się założenie najprostsze do chwili ewentualnego wykazania, że nie jest to poprawne. Wprawdzie potęga "2" może być równie dobra z punktu widzenia doświadczenia jak "1,999999", lecz operacje na dwójce są znacznie prostsze. Chciałoby się powiedzieć, że 2 przełyka się gładko, a 1,999999 jak jeża. Co więcej, w wypadku "2" rozwiązanie problemu ruchu w układzie dwu ciał jest wyjątkowo piękne: otrzymujemy ruch po jednej z krzywych stożkowych, np. po elipsie, ustalonej w przestrzeni. Każde odstępstwo od 2 powoduje, że na ruch ten nakłada się ruch inny, ruch obrotu tej elipsy w tej płaszczyźnie, co powoduje, że ruch wypadkowy odbywa się po krzywej rozetkowej. Lecz cóż, natura jest przekorna. Okazuje się, że rzeczywisty ruch w polach Newtona i Coulomba jest właśnie ruchem rozetkowym. Mimo to jednak odrzucamy możliwość odstępstwa od 2, wyjaśniając istnienie obrotu elipsy efektami relatywistycznymi. Mianowicie, na tej części elipsy, która leży bliżej ogniska odpowiadającego centrum sił, ciało poruszające się (Ziemia czy też elektron) porusza się szybciej, a więc ma nieco większą masę, zgodnie z zasadami teorii względności, niż w tej części elipsy, która jest odległa od centrum sił. Pociąga to za sobą konsekwencje co najmniej kinematyczne (w polu Coulomba) lub nawet dynamiczne (w polu Newtona), co wpływa ostatecznie na zmianę ruchu eliptycznego na rozetkowy. Czemu jednak przemawia do nas to wyjaśnienie, a nie zdobyło sympatii prawo "1,999...9"? Co najmniej z dwu powodów. Po pierwsze, teoria względności poza ruchem rozetkowym wyjaśnia wiele innych zjawisk, istnieje więc tutaj wiele dodatkowych testów, które teoria ta zwycięsko "zaliczyła". Natomiast "1,999...9" jest wymyślone ad hoc do jednego zjawiska i trudno znaleźć inne mierzalne konsekwencje tego prawa. Po drugie zaś "1,999...9" jest po prostu brzydkie. Od czasów Pitagorasa, słusznie czy nie, przyjemniej zawsze jest obcować z liczbami całkowitymi. Tak więc prawo "1,999...9" odpada z konkurencji ze względu na kryterium prostoty, kryterium piękna, kryterium większej ogólności (a więc i lepszej sprawdzalności) teorii konkurencyjnych.

Kryterium większej ogólności tłumaczy nam też, dlaczego do ruchu jabłka i do ruchu Księżyca nie budujemy oddzielnych teorii. Każda z dwu teorii, "jabłkowa" i "księżycowa", miałaby mniejszy zakres stosowalności niż teoria jednolita. Teoria ta ujawnia nam poza tym uderzającą jedność przyrody, jest po prostu piękna.

Przygody teorii Newtona z układem planetarnym są równie pouczające. Obserwując zakłócenia w ruchu Urana, wprowadzono dodatkową hipotezę o istnieniu dalszej planety. Hipoteza ta ma niezależny sprawdzian, a mianowicie po prostu przewiduje ona wykrycie tej nowej planety. Skoro odkrycie to nastąpiło, hipoteza została sprawdzona i przyjęta. Natomiast Wulkana po prostu nie ma, a przyjęcie smugi rzadkiej materii nie dostarcza dodatkowego sprawdzianu, skoro smugi tej nie można wykryć obserwacyjnie. Koncepcję tę należało więc odrzucić i czekać na inne rozwiązanie zagadki. Podał je Einstein dopiero w roku 1915.

No i wreszcie nasza ciągłość. Jest to problem ciekawy i znacznie bardziej skomplikowany, niż mogłoby się wydawać. Jest przecież faktem, że w ogromnej większości przypadków posługujemy się w formalizmie fizyki funkcjami ciągłymi. Co nas do tego zmusza? Czy po prostu lubimy ciągłość?

Ze względów czysto rachunkowych ciągłość ma niewątpliwą przewagę nad nieciągłością. Posługując się funkcjami ciągłymi, możemy korzystać z rachunku różniczkowego i całkowego. Znacznie łatwiej jest posługiwać się pochodną, a dokładniej różniczką, niż skończoną różnicą, wygodniej jest całkować niż sumować szeregi, prościej rozwiązywać równania różniczkowe niż różnicowe. Mamy więc dla ciągłości jeden punkt: prostotę i wygodę.

Należy jednak odróżnić ciągłość w przyrodzie od ciągłości funkcji służących do jej opisu. Czy wiemy coś o ciągłości przestrzeni i czasu? (Właściwym terminem matematycznym byłoby tu pojęcie zupełności, gdyż ciągłość jest cechą nie zbiorów, lecz odwzorowań. Pozostanę jednak przy mniej dokładnym, lecz bardziej naocznym i potocznym terminie).

Na pierwszy rzut oka można by sądzić, że ciągłość przestrzeni i czasu przeżywamy bezpośrednio w doświadczeniu, czy to zmysłowym, czy też introspekcyjnym. Ciała, jak się nam wydaje, zajmują w kolejnych chwilach kolejne położenia w sposób ciągły. Jednakże, jak świadczy przykład kina, wniosek taki nie jest uprawniony, gdyż nasz układ nerwowy samodzielnie łączy bliskie chwile i bliskie punkty w ciągłe całości. Co więcej, badania nad tym układem (np. nad wzrokiem i widzeniem) wskazują, że w ogóle nie może on odbierać i przekazywać informacji w sposób ciągły. Informacja taka w nerwie jest pewną salwą wyładowań elektrycznych, do której dochodzi tylko wtedy, gdy bodziec jest dostatecznie silny. Dzieląc zaś ciągłe zjawisko na bardzo krótkie fazy, zbieralibyśmy z każdej z nich nikły bodziec o wartości podprogowej, w granicy nawet nieskończenie mały. Układ nerwowy dokonuje więc "całkowania" bodźców po skończonych odcinkach i nie może wewnątrz takich odcinków dostrzec żadnej natury. Tak więc, mimo bezpośredniego przeżycia ciągłości, widzimy, że nie ma ona nic wspólnego z tym, co jest "naprawdę". W tej sytuacji możemy jeszcze szukać jakichś pośrednich dowodów ciągłości bądź nieciągłości czasu i przestrzeni. Na przykład, gdyby teorie fizyczne oparte na założeniu ciągłości napotykały jakieś zasadnicze trudności, z którymi byłaby za to zdolna sobie poradzić teoria dyskretnej przestrzeni lub czasu, byłby to właśnie taki pośredni dowód, przemawiający za nieciągłością tych struktur. Jednakże, jak dotąd, sytuacja taka nie zachodzi. Wobec tego przyjmujemy ciągłość za normę, a nieciągłość za anomalię, wymagającą za każdym razem, gdyby się pojawiła, jakiegoś wyjaśnienia. Idziemy tu zarówno za prostotą i wygodą "ciągłościowego" aparatu matematycznego, jak i za "uciąglającą" działalnością naszego aparatu zmysłowego, która skłania nas do traktowania tego, co ciągłe, jako coś naturalnego. To przekonanie odbija się w takich powiedzeniach, jak np. "natura nie czyni skoków" lub, ogólniej, "każda zmiana ma swoją przyczynę".

Ostatniego sformułowania nie można brać dosłownie. Filozofowie greccy ze szkoły eleatów próbowali wejść na tę drogę i przeprowadzili następujące rozumowanie. "Przyczyna jest czymś zewnętrznym względem skutku. Poza tym, co jest, nie ma niczego. Każda zmiana musi mieć swoją przyczynę. A więc to, co jest, musi być absolutnie niezmienne, gdyż poza nim nie ma niczego, co by mogło być przyczyną zachodzących w nim zmian". Eleaci uznali konsekwentnie wszelki ruch i wszelką zmienność za złudzenie i wymyślili szereg pomysłowych a paradoksalnych argumentów, świadczących ich zdaniem o tym, że ruch jest czymś wewnętrznie sprzecznym, a więc nie może zachodzić.

Jeśli więc nie chcemy posunąć się tak daleko, musimy uznać, że pewna zmienność nie wymaga działania przyczyny. Przykładem może być ruch jednostajny prostoliniowy, który w układzie inercjalnym zachodzi bez działania żadnej siły. W tym przypadku oczywiście przyspieszenie także równe jest zeru.

Można sobie zadać pytanie, co w aparacie teoretycznym fizyki zapewnia nam ciągłość prędkości. Odpowiedź jest bardzo prosta. Zawdzięczamy to bezwładności materii, tkwiącemu w niej sprzeciwowi względem wprowadzanych do jej stanu zmian. Taka bezwładność w uogólnionym sensie występuje w różnych działach fizyki. Przykładowo można tu wymienić zjawisko samoindukcji, które sprzeciwia się skokowej zmianie natężenia prądu pod wpływem skokowej zmiany napięcia. Podobną rolę w termodynamice odgrywa znana zasada przekory Le Chatelier-Brauna. Wydaje się więc, że w samej materii tkwią mechanizmy "uciąglające", które nie dopuszczają do skokowych zmian pewnych wielkości fizycznych.

Koncepcja bezwładności wiąże się jednakże, co warto zauważyć, z infinitezymalną koncepcją związku skutkowo-przyczynowego. Przyczyna poprzedza skutek, mówiąc obrazowo, o 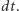Aby tego rodzaju koncepcję zrealizować, potrzebna jest ciągła natura czasu (zupełność zbioru chwil), o której poprzednio mówiliśmy.

Skądinąd wspominając poprzednio o "skokowym" narastaniu siły, pominęliśmy fakt, że w rzeczywistości włączenie siły może także nastąpić tylko w sposób ciągły. Wiąże się ono przecież z dostarczeniem do określonego punktu określonego źródła siły: masy, ładunku elektrycznego itp. To zaś, jak każdy ruch, zachodzi ze skończoną prędkością, a więc odpowiednia siła musi narastać stopniowo.

Mógłby ktoś argumentować, że fizyka klasyczna niejednokrotnie korzysta z pojęć nieciągłych. Mówi się o nieciągłości w przypadku zmian stanu skupienia; zachodzi wtedy nieciągła zmiana gęstości. Innym przykładem mógłby być "skok" pola elektrostatycznego na powierzchni przewodnika. (Istnienie takiego skoku wynika z prawa Gaussa). Pole bowiem wewnątrz naładowanego przewodnika znika, a na zewnątrz ma wartość niezerową. Wielkość skoku można powiązać z gęstością ładunku znajdującego się na powierzchni przewodnika.

Jednakże w obu przypadkach nie może być mowy o rzeczywistej nieciągłości. Nie jest przecież tak, że w pewnej chwili całe ciało jest stałe, a w następnej chwili już ciekłe. Topnienie zajmuje pewien czas, a przebieg tego procesu w mikroskali określony jest przez mikrostruktury ciała topniejącego: rozmaite defekty, zanieczyszczenia itd. Dynamika procesu topnienia jest więc skomplikowana i często, z punktu widzenia efektu końcowego, zupełnie nieistotna. W takich przypadkach cały ten proces zastępujemy "skokiem", zwężając czas jego trwania do zera.

Drugi z wymienionych wyżej przykładów "skoków" w fizyce zawiera w sobie przypuszczenie, że ładunki elementarne (np. elektrony) są obiektami punktowymi. Gdyby tak istotnie było, mogłyby one zajmować położenia wyłącznie na powierzchni przewodnika, zakładając, oczywiście, że powierzchnię tę da się rzeczywiście w mikroskali dokładnie określić. Wprawdzie nie wiemy jeszcze wiele o wewnętrznej budowie elektronu, ale wiemy na pewno, że nie jest to cząstka punktowa. Lepiej znamy budowę wewnętrzną protonu. Okazuje się, że ładunek elektryczny w tej cząstce rozłożony jest w sposób ciągły, a nie ma powodu przypuszczać, by w elektronie sprawy miały się inaczej. W takiej sytuacji elektrony nie zajmują samej tylko powierzchni przewodnika, lecz tworzą warstwę pewnej grubości na tej powierzchni, w której zachodzi ciągła zmiana pola. Dodać trzeba, że poza tym część elektronów jest emitowana z przewodnika do otaczającej go przestrzeni, co dodatkowo "uciągla" rozkład ładunku, a więc i pola elektrycznego. Jednakże grubość tej warstwy z mikroskopowego punktu widzenia jest tak mała, że najczęściej opłaca się pominąć tę grubość i traktować problem "skokowo".

No, ale w zjawiskach kwantowych, powie ktoś, nieciągłość na pewno da się odnaleźć. Rzeczywiście, wydaje się, że tak jest istotnie. Weźmy atom wodoru, rozważmy go jako układ proton-elektron. W stanie związanym (gdy składniki pozostają zawsze w skończonej odległości od siebie) układ ten może mieć, zgodnie z równaniem Schrödingera, jedynie ściśle określone, dyskretne wartości energii. A więc nieciągłość - nareszcie - wykryta! Ale uwaga! Wśród tych, jak mówimy, poziomów energetycznych jeden tylko jest trwały, ten który odpowiada najniższej energii. Wszystkie wyższe nie są trwałe, gdyż z emisją fotonu "rozpadają się" one, przechodząc do stanów niższych. Zgodnie zaś z zasadami tejże mechaniki kwantowej, układ fizyczny nietrwały nie może mieć dokładnie określonej energii (podobnie jak układ o określonym pędzie nie może mieć dokładnie określonego położenia), przy czym iloczyn średniego czasu życia przez nieokreśloność energii jest rzędu stałej Plancka 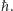Dyskretne poziomy energii ulegają więc rozmyciu, czy też poszerzeniu, i ciągłość zostaje przywrócona. Co prawda, nie dotyczy to poziomu najniższego, ale tylko w przypadku pojedynczego odosobnionego atomu. W zwykłym gazie, choćby bardzo rozrzedzonym, przejścia między poziomami energii zachodzą nie tylko w wyniku emisji fotonów, ale też w wyniku zderzeń międzyatomowych, które powodują dwukierunkowy przepływ energii - od energii kinetycznej ruchu atomów do energii wewnętrznego ruchu elektronów w poszczególnych atomach i na odwrót. W rezultacie wszystkie poziomy energetyczne ulegają dodatkowemu poszerzeniu. A więc i tu mamy do czynienia z przebiegami ciągłymi. Właściwie jedyną rzeczą naprawdę nieciągłą w świecie mechaniki kwantowej jest to, czego w niej najbardziej nie rozumiemy. Mam na myśli akt pomiaru. Weźmy jako przykład elektron, poruszający się z ustalonym pędem, a więc mający całkowicie nie ustalone położenie. Wyobraźmy sobie teraz, że na elektronie tym wykonujemy pomiar jego położenia. W rezultacie sytuacja skokowo zmieni się: położenie elektronu zostanie ustalone, ale jego pęd utraci swą dotychczasową wartość, stając się wielkością mniej lub bardziej nieokreśloną, zależnie od tego, jak dokładnie określiliśmy położenie elektronu. W rzeczywistości akt pomiaru zajmuje jakiś czas i tkwi za tym jakiś efekt fizyczny. Nie jest on jednak ujmowany w formalizmie mechaniki kwantowej, co chyba należy uważać za jej najsłabszy punkt od strony pojęciowej.

Uwagi te można by jeszcze rozwinąć. Wydaje mi się jednak, że już to, co tu zostało powiedziane, wystarcza do sformułowania następujących wniosków. Po pierwsze, w fizyce, jak i w każdej innej nauce przyrodniczej, tkwi szereg założeń metodologicznych, nie usprawiedliwionych metodami uznawanymi za poprawne przez tę naukę. Wymieniliśmy tu wygodę, prostotę, piękno, intersubiektywność, ogólność (większa sprawdzalność), a listę tę można by przedłużyć. Zagadnienie ciągłości zwraca nam uwagę na dodatkowy kapitalny fakt: że w budowie aparatu pojęciowego nauki jesteśmy także uwarunkowani charakterem naszego aparatu zmysłowego. Niezależnie od złożoności formalizmu, gdzieś, kiedyś przychodzi moment, że chcemy sobie wyobrazić zjawiska formalizmem tym opisywane. I tu łatwiej przychodzi nam zdecydować się na rozwiązania "wyobrażalne" niż na te, które są sprzeczne ze strukturą naszego umysłu i aparatu zmysłowego. Tak właśnie postępujemy, przyjmując ciągłość za normę. Starałem się wykazać, że takie założenie w odniesieniu do przestrzeni i czasu niemal automatycznie pociąga za sobą ciągłość naszego obrazu zjawisk fizycznych. Pozostaje nierozstrzygnięte, nieco może metafizyczne pytanie, czy "uciąglająca" natura naszego aparatu zmysłowego jest jakimś po prostu ułatwieniem technicznym, czy też jest genetycznie dostosowana do prawdziwej, głębokiej ciągłości natury.