Drobiazgi
Mała Delta
Do przemyślenia na plaży i nie tylko

Dodatkowe ciśnienie pary wodnej
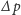 jest równe ciśnieniu warstwy
wody, która wzięłaby się z pokrycia całej powierzchni Ziemi warstwą wody
z oceanów o stałej grubości. Średnia głębokość oceanów wynosi
jest równe ciśnieniu warstwy
wody, która wzięłaby się z pokrycia całej powierzchni Ziemi warstwą wody
z oceanów o stałej grubości. Średnia głębokość oceanów wynosi
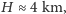 można założyć, że zajmują one
można założyć, że zajmują one
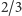 powierzchni
Ziemi. Zatem
powierzchni
Ziemi. Zatem
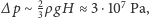 czyli ciśnienie wzrosłoby ponad
100 razy.
czyli ciśnienie wzrosłoby ponad
100 razy.
Jadąc na nartach wodnych, można się utrzymać na powierzchni wody,
jeśli siła ciężkości, działająca na poruszającego się na nich człowieka,
równa jest pionowej składowej siły działania wody na narty. Jest ona
proporcjonalna do
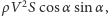 gdzie
gdzie
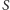 – powierzchnia nart,
a
– powierzchnia nart,
a
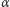 to kąt nachylenia nart do horyzontu. Pomijając siłę wyporu, dla
to kąt nachylenia nart do horyzontu. Pomijając siłę wyporu, dla
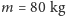 i
i
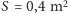 otrzymujemy:
otrzymujemy:
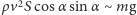 ,
,
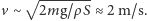
Problem 3. Jakiej głębokości dołek utworzy się pod śmigłowcem ratowniczym, który zawisł na niewielkiej wysokości nad wodą daleko od brzegu?
Ze względu na panującą równowagę powietrze działa od dołu na śmigłowiec
siłą skierowaną w górę i równą sile ciężkości działającej na śmigłowiec.
Warstwa powietrza między śmigłowcem a wodą przy niezbyt dużej
wysokości z taką samą siłą działa na wodę, tworząc zagłębienie. Zatem
śmigłowiec wypchnie taką masę wody, jaką ma on sam (powietrze między nim
a wodą odgrywa rolę elementu przenoszącego siłę i może być pominięte
w rozważaniach). Przyjmując masę śmigłowca równą
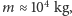 długość śmigieł
długość śmigieł
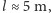 otrzymujemy głębokość dziury równą
w przybliżeniu
otrzymujemy głębokość dziury równą
w przybliżeniu
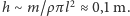
Przyjmijmy, że prędkość rowerzysty na finiszu wynosi
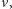 a siła oporu
powietrza
a siła oporu
powietrza
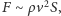 gdzie
gdzie
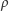 to gęstość powietrza, a
to gęstość powietrza, a
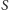 –
efektywne pole powierzchni kolarza, na które pada prąd powietrza. Stąd moc
–
efektywne pole powierzchni kolarza, na które pada prąd powietrza. Stąd moc
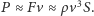 Przyjmując
Przyjmując
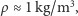
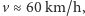
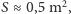 otrzymujemy
otrzymujemy
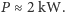
Porównajmy moment sił:
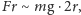 gdzie
gdzie
 to promień koła
zębatego,
to promień koła
zębatego,
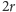 – odległość pedału od osi tego koła,
– odległość pedału od osi tego koła,
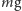 – siła
ciężkości działająca na człowieka równa maksymalnej sile nacisku na pedał.
Dla
– siła
ciężkości działająca na człowieka równa maksymalnej sile nacisku na pedał.
Dla
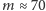 kg otrzymujemy
kg otrzymujemy
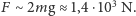
Problem 6. W jakiej odległości od obserwatora człowiek w jaskrawym ubraniu, uciekający przez las (bez poszycia), przestaje być widoczny?
Niech
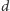 oznacza średni promień pnia drzew, a
oznacza średni promień pnia drzew, a
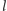 – średnią
odległość między drzewami. Dokonajmy pewnego eksperymentu myślowego
i rozmieśćmy drzewa tak, żeby tworzyły ścisłą palisadę w kształcie okręgu
o promieniu równym szukanej odległości
– średnią
odległość między drzewami. Dokonajmy pewnego eksperymentu myślowego
i rozmieśćmy drzewa tak, żeby tworzyły ścisłą palisadę w kształcie okręgu
o promieniu równym szukanej odległości
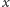 z obserwatorem w jego
środku. Za taką palisadą nawet człowiek w jaskrawym ubraniu nie będzie
widoczny. W ogrodzeniu długości
z obserwatorem w jego
środku. Za taką palisadą nawet człowiek w jaskrawym ubraniu nie będzie
widoczny. W ogrodzeniu długości
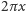 jest więc
jest więc
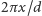 drzew,
które zostały wzięte z obszaru o powierzchni
drzew,
które zostały wzięte z obszaru o powierzchni
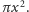 Jeśli na obszar
Jeśli na obszar
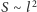 przypada średnio jedno drzewo, to na powierzchni
przypada średnio jedno drzewo, to na powierzchni
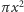 będzie ich
będzie ich
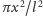 . Zatem
. Zatem
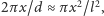 skąd, przyjmując
skąd, przyjmując
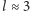 m i
m i
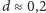 m, dostajemy
m, dostajemy