Aktualności (nie tylko) fizyczne
Fizyczne uwarunkowanie obliczeń
Każde (niekwantowe) obliczenie wymaga użycia serii nieodwracalnych
operacji logicznych, w których dwa stany wejściowe dają jeden stan końcowy.
Przykładem takiej operacji jest zerowanie komórki pamięci. W 1961 roku
Rolf Landauer wykazał, że minimalna ilość ciepła, porównywalna z
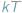 (gdzie
(gdzie
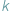 jest stałą Boltzmana, a
jest stałą Boltzmana, a
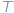 temperaturą w skali
bezwzględnej), jest do tego niezbędna [1]. Ograniczenie
temperaturą w skali
bezwzględnej), jest do tego niezbędna [1]. Ograniczenie
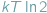 jest
obecnie nazywane granicą Landauera, która określa nieprzekraczalne fizyczne
ograniczenie minimalnej ilości ciepła rozpraszanego podczas pojedynczej
nieodwracalnej operacji logicznej dowolnego dwójkowego urządzenia.
jest
obecnie nazywane granicą Landauera, która określa nieprzekraczalne fizyczne
ograniczenie minimalnej ilości ciepła rozpraszanego podczas pojedynczej
nieodwracalnej operacji logicznej dowolnego dwójkowego urządzenia.
Jednakże, pomimo zasadniczego znaczenia dla rzeczywistych implementacji obliczeń informatycznych, ta podstawowa zasada nie została, do niedawna[2], doświadczalnie sprawdzona. Głównym powodem były techniczne trudności eksperymentowania z pojedynczą komórką pamięci w tak niskim zakresie rozpraszanej energii, ale nie mniej istotne były wątpliwości co do poprawności oraz użyteczności ograniczenia. Przecież rozpraszanie energii w obecnie używanych krzemowych układach cyfrowych jest trzy rzędy wielkości ponad ograniczenie Landauera. Z drugiej strony jednak, osiągnięcie tego limitu jest spodziewane wraz z postępującą miniaturyzacją układów scalonych.
Doświadczalne potwierdzenie realności ograniczenia Landauera w przykładowym modelu jednobitowej pamięci zostało uzyskane[2] dla pojedynczej koloidalnej cząstki uwięzionej w podwójnej studni potencjału o regulowanych parametrach. Zostało wykazane, że średnia rozpraszana energia zmniejsza się wykładniczo z wydłużającym się czasem operacji, asymptotycznie zbiegając do granicy Landauera.