Nie można bezkarnie powiększać dzieci!

Powiększanie i zmniejszanie

W filmie pt. „Kochanie, powiększyłem dzieciaka” genialny wynalazca skonstruował urządzenie mogące powiększać i zmniejszać przedmioty. Treścią filmu są kłopoty, jakie się pojawiają w związku z przypadkowym, kilkudziesięciokrotnym powiększeniem dziecka. Chciałbym tu przestrzec wszystkich przed powiększaniem w ten sposób swoich dzieci – mogą pojawić się zupełnie inne problemy, niż te pokazane w filmie. Jeśli założymy, że mięśnie i kości powiększonego dziecka nie różnią się znacząco od zwykłych mięśni i kości, a przez 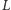oznaczymy wzrost dziecka, to stwierdzimy, że:

• siła ręki jest proporcjonalna do jej pola przekroju poprzecznego, czyli do 
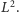
• ciężar ręki jest proporcjonalny do jej objętości, a więc do 

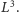
Zatem stosunek siły ręki do jej ciężaru jest proporcjonalny do 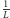 – oznacza to, że nasze powiększone dziecko może nie być w stanie wykonać żadnego ruchu, a być może nawet załamią się pod nim jego kości!

Przykład z powiększaniem dziecka jest może bardzo odległy od realiów, ale taką samą analizę możemy przeprowadzić np. w przypadku mostów: nie powinniśmy w taki sam sposób budować kładki przez strumyk i mostu przez dużą rzekę, a fakt, że kartonowy model budynku może być bardzo trwały, nie oznacza, iż w taki sam sposób powinniśmy budować prawdziwe budynki.

Jest wiele przykładów otrzymywania ciekawych i często nieoczekiwanych rezultatów na podstawie analizy zależności od rozmiarów (dalej będziemy mówili – zależności od skali). Oto dwa przykładowe problemy:

Przed słoniem należy uciekać pod górę!

Wielkość stworzenia nie ma wpływu na wysokość skoku.

• Jak zależy szybkość wbiegania zwierzęcia pod górę od jego rozmiarów?
  Tu wynik jest nieoczekiwany: im mniejsze zwierzę, tym łatwiej mu wbiegać. Choć może nie jest to aż tak zaskakujące, jeśli pamięta się o psach wbiegających z werwą na górkę i jednocześnie ich właścicielach, mających wielkie problemy z wejściem na nią. W każdym razie, jeśli kiedyś będzie nas gonił słoń, to pamiętajmy, żeby uciekać pod górę!
• Jak zależy wysokość skoku zwierzęcia od jego rozmiarów?
  Tu wynik też wydaje się dziwny – po prostu nie zależy! Inaczej mówiąc: pchła, pies, człowiek i koń mają w skoku wzwyż takie same szanse! Dlaczego zatem skoczkowie wzwyż są wysocy, a jeszcze wyżsi są koszykarze? Po prostu wyższy ma wyżej środek ciężkości i wyżej dosięga bez podskakiwania.

Oczywiście, powinniśmy zdawać sobie sprawę z wielkich uproszczeń w analizie rozważanych zagadnień: przecież pies nie jest po prostu zmniejszonym człowiekiem, a już na pewno nie można tego powiedzieć o pchle. Zresztą w przypadku pchły przegapiliśmy bardzo ważny problem, z jakim ma ona do czynienia przy skakaniu: podczas gdy dla nas opór powietrza nie ma żadnego wpływu na wysokość skoku, dla niej jest on wielkim problemem!

Te przykłady pokazują, że bardzo ogólne rozważania dotyczące zależności od skali może nas doprowadzić do ciekawych wniosków. W szczególności opis zagadnienia może znacznie się uprościć, jeżeli potrafimy go sformułować tak, aby od skali nie zależał.

Skalowanie – niezależność od skali

Najprostszym przykładem jest tu czysta, gładka kartka papieru. Gdy patrzymy na nią z różnej odległości, to ma ona dla nas różne rozmiary. Jeśli jednak zaczniemy się jej przypatrywać z bardzo bliska (wyobraźmy sobie, że jesteśmy naszą znajomą pchłą siedzącą sobie na tej kartce), to to, czy jest to kartka rozmiaru A4, A3, czy jeszcze większa, nie będzie miało dla nas żadnego znaczenia! Oczywiście pod warunkiem, że nie będziemy tak blisko niej, żeby zobaczyć jej nierówności, czy może nawet atomy, z których jest zbudowana. Inaczej mówiąc, jest pewien zakres „powiększeń”, w którym kartka papieru jest dla nas nieskończoną płaszczyzną, a powiększona lub zmniejszona płaszczyzna (podobnie jak prosta) pozostaje sobą.

Niezależność od skali oznacza, że powiększony fragment wygląda tak jak całość.

Ten przykład wydaje się nieciekawy i bez znaczenia praktycznego, ale… Na przykład wydarzyło się wiele wypadków wodnosamolotów (hydroplanów) lądujących na morzu – po prostu pilot nad spokojnym morzem ma bardzo duże problemy ze wzrokową oceną wysokości, na jakiej się znajduje.

Bardzo ciekawymi obiektami, „pozostającymi sobą” przy powiększaniu, są fraktale: są one tak skonstruowane, że ich fragment jest zmniejszeniem całości. Oczywiście, dotyczy to tylko idealnych, czysto matematycznych obiektów – malutki fragment narysowanego fraktala jest już tylko małą plamką, a nie pomniejszeniem całości.

Punkt krytyczny i grupa renormalizacyjna

Wszystkie dotychczas rozważane zagadnienia wydają się stosunkowo proste. Teraz jednak przejdziemy do dużo trudniejszego problemu, związanego z… parowaniem wody. Nie każdy zdaje sobie sprawę z tego, że między parą a cieczą nie ma „istotnych” różnic (ale już między wodą a lodem są). Jak to nie ma: przecież para jest lekka, a ciecz ciężka (ma gęstość około tysiąca razy większą niż para)? No dobrze, ale jeśli rozpatrzymy parę sprężoną tysiąc razy i ciecz pod ciśnieniem 1000 atmosfer, to może już nie być różnicy gęstości (ciecz jest praktycznie nieściśliwa). Jak, nawet w takiej sytuacji, odróżnić ciecz od pary? Najprostsza odpowiedź jest taka: para to jest to, co powstaje (jak sama nazwa na to wskazuje) przy parowaniu cieczy. A parowanie to taki proces, w którym musimy dostarczać ciepło, a temperatura się nie zmienia (po zgaszeniu gazu woda w czajniku niemal natychmiast przestaje wrzeć). Inaczej mówiąc, nawet jeśli nie wiemy, co jest cieczą, a co jest parą, to możemy doprowadzić do sytuacji, w której w tej samej temperaturze mamy jednocześnie i ciecz, i parę, czyli dwie różne fazy tej samej substancji.

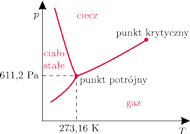
Wykres fazowy dla wody.

Okazuje się jednak, że w odpowiednio dużej temperaturze nie możemy mieć jednocześnie i cieczy, i pary, a właściwie ciecz i para jest tym samym (mamy tylko jedną fazę). Oznacza to, że zamiast odparowywać wodę możemy zrobić tak: zwiększamy odpowiednio jej ciśnienie, podgrzewamy, potem zmniejszamy ciśnienie do początkowego, a następnie obniżamy temperaturę. W efekcie, pokonując nieco okrężną drogę, otrzymamy parę, mimo iż na żadnym etapie tego procesu nie było parowania (warto podkreślić, że takiej sztuczki nie możemy zrobić, aby z wody otrzymać lód – tu zawsze pojawi się sytuacja, w której zamrażamy wodę).

Najwyższą temperaturę i odpowiadające jej ciśnienie, przy których jeszcze mogą współistnieć ze sobą ciecz i para, nazywamy punktem krytycznym.

I tu wracamy do głównego nurtu tej opowieści. Okazuje się, że wiele własności substancji w pobliżu punktu krytycznego nie zależy od skali. Na przykład, jeśli odpowiednio sprytnie zrobimy zdjęcie naszej substancji, to otrzymamy niemal taki sam obraz niezależnie od powiększenia (oczywiście w pewnym zakresie powiększeń). No, ale co może być widać na takim zdjęciu? Ciemniejsze fragmenty odpowiadające miejscom, gdzie nasza substancja jest nieco gęstsza, i jaśniejsze odpowiadające miejscom, gdzie jest rzadsza. Skąd się biorą takie różnice w gęstości? Są one po prostu wynikiem przypadkowego ruchu i przypadkowego skupiania się cząstek. W punkcie krytycznym wielkość i ilość ciemniejszych plam (oczywiście średnio) nie będzie zależna od skali (czyli powiększenia naszego zdjęcia).

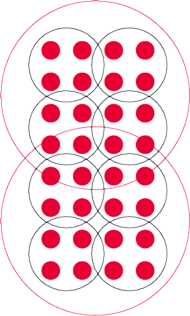
Graficzna reprezentacja procedury tworzenia „nowych atomów” opisanej w tekście.

To, co się dzieje w okolicy punktu krytycznego, czyli tzw. zjawiska krytyczne, interesowało fizyków od bardzo dawna, jednak przez długi czas teoretyczne modele w tej dziedzinie były nieudane. Dopiero zastosowanie rozumowania opartego na badaniu zależności od skali przyniosły tu znaczący postęp. Idea takich modeli jest następująca.

Wyobraźmy sobie substancję jako układ atomów połączonych sprężynkami. Sprężynki mogą łączyć nie tylko najbliższe atomy, ale i dalsze, np. pierwszy z piątym, drugi z szóstym itp. (ściślej mówiąc, zamiast o sprężynkach powinniśmy mówić o „sprzężeniach” między atomami). Teraz zróbmy pierwszy (choć może na pierwszy rzut oka absurdalny) krok: utwórzmy zespoły atomów składające się z (na przykład) czterech najbliższych sąsiadów i każdy taki zespół potraktujmy jako nowego rodzaju atom. Inaczej mówiąc, zapomnijmy o tym, co jest wewnątrz naszego zespołu (nowego rodzaju atomu) i patrzmy jedynie na to, jak takie zespoły oddziałują ze sobą. W rzeczywistości jeden zespół łączy się z drugim za pomocą wielu sprężynek (wychodzących z atomów będących składnikami takiego zespołu), a my je wszystkie zastępujemy jedną, odpowiednio dobraną. Po wykonaniu tego kroku mamy sytuację bardzo podobną do wyjściowej: znowu mamy atomy (choć nie są to już prawdziwe atomy) połączone sprężynkami. Teraz możemy zrobić następny krok: nowe „atomy” łączymy w zespoły, które znowu nazywamy atomami i wprowadzamy nowe sprężynki łączące nowe atomy. Taką procedurę możemy powtarzać wielokrotnie. Podstawowym problemem przy tym podejściu jest tłumaczenie własności „starych” sprężynek na własności „nowych”. Oczekujemy, że w pobliżu punktu krytycznego, ze względu na niezależność „wyglądu” substancji od skali, takie tłumaczenie jest takie samo w pierwszym kroku, jak i w pięćdziesiątym. A to już pozwala napisać równania, z których można wiele się dowiedzieć o badanej substancji.

Oczywiście, zastosowanie w praktyce opisanej procedury, zwanej metodą grupy renormalizacyjnej, jest bardzo trudne: aby móc cokolwiek obliczyć, trzeba dokonać wielu przybliżeń, pojawiają się dodatkowe problemy. Jednak w ten sposób fizycy potrafią obliczyć to, co było dla nich nie do obliczenia innymi sposobami!

Fizyka cząstek elementarnych

Przejdźmy teraz do następnego przykładu – opisu oddziaływań między cząstkami elementarnymi.

Wszelkie zjawiska elektromagnetyczne – rozchodzenia się fal radiowych, odpychanie lub przyciąganie ładunków – można wyjaśnić, wychodząc od elementarnego procesu oddziaływania naładowanej cząstki (np. elektronu) z fotonem. To, jaką „szansę” na pochłonięcie lub wysłanie fotonu ma elektron, jest określone przez pewną stałą, zwaną stałą sprzężenia elektromagnetycznego (oznaczamy ją literą 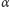 i jest ona w przybliżeniu równa 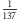). Ta stała jest bezwymiarowa, co sugeruje niezależność wartości sprzężenia elektromagnetycznego od skali, okazuje się jednak, że rzeczywistość jest bardziej skomplikowana.

To skomplikowanie związane jest z nieskończonościami, jakie pojawiają się w teoriach opisujących podstawowe oddziaływania.

Zacznijmy od prostego przykładu: jeśli elektron potraktujemy jako naładowaną kulkę o promieniu 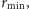to jego energia elektromagnetyczna jest proporcjonalna do 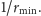 Jeśli elektron jest cząstką fundamentalną, nieskładającą się z innych cząstek (na razie nie mamy podstaw, by myśleć inaczej), to jego promień powinien być równy 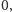a to wiąże się z nieskończoną energią elektromagnetyczną.

Powyższy wynik opiera się na obliczeniach klasycznych. Uwzględnienie mechaniki kwantowej (a właściwie kwantowej teorii pola) zmienia obraz. Można powiedzieć, że mechanika kwantowa zmusza nas do włączenia procesu pomiaru do opisu badanego zjawiska. Badając coraz mniejsze odległości, „zmuszeni” jesteśmy używać „sond”, fotonów o coraz mniejszych długościach fali. Im mniejsza długość fali, tym większa energia fotonu i tym większe prawdopodobieństwo, że foton zamieni się w wirtualną parę elektron-pozyton. Te cząstki z kolei mogą wyświecać wirtualne fotony i tak odsłania się przed nami pewna samopodobna struktura.

To jednak jeszcze nie rozwiązuje naszego problemu. Choć dla małych 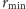 wartość energii elektromagnetycznej elektronu jest dużo mniejsza niż w przypadku klasycznym, to nadal staje się ona nieskończona, gdy 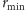staje się równe

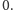
• Przed renormalizacją sekretarka zarabia 3000 zł pensji podstawowej i to są jej wszystkie przychody.
• Po renormalizacji dyrekcja postanowiła osobno wycenić podstawowe czynności sekretarki i prace dodatkowe (np. podawanie kawy). Od tej pory sekretarka zarabia 2000 zł pensji podstawowej, zwanej „gołą pensją”, i 1000 zł dodatku.

Co ma jednak zrobić dyrektor, dla którego to właśnie dodatkowe czynności sekretarki mają największą, wręcz nieocenioną (nieskończoną?) wartość? Wystarczy, że wyceni tak podstawowe czynności sekretarki, żeby w sumie, „na rękę”, sekretarka dostawała nadal 3000 zł, nie przejmując się, że w tym przypadku „goła” pensja będzie dużą liczbą ujemną.

Jeśli wrócimy do przykładu z elektronem, to powyższa procedura sprowadzi się do następującego rozumowania. Przyjmujemy, że promień elektronu wynosi 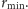 Obliczmy, ile wynosi energia elektromagnetyczna elektronu przy takim promieniu, a potem dobieramy tak energię spoczynkową „gołego” elektronu
(tzn. elektronu bez otaczającego go pola elektrycznego), żeby w sumie wyszło to, co mierzymy w doświadczeniu.

W naturalny sposób pojawia się tu pytanie: skoro po całej tej procedurze otrzymaliśmy to, co mieliśmy na początku (bo zmierzyliśmy w doświadczeniu), to może nie warto było jej w ogóle przeprowadzać? Żeby się przekonać, że jednak było warto, rozważmy następującą sytuację.

Podobna sytuacja występuje przy obliczeniach w fizyce cząstek elementarnych – wprawdzie dobieramy tak nasze parametry, żeby pewne obliczone wielkości miały zadaną z góry wartość, ale możemy też obliczać zupełnie inne rzeczy.

A co z tytułowym pytaniem? Co prawda, nie znaleźliśmy na nie odpowiedzi, ale już wiemy, że przy opracowywaniu sposobów radzenia sobie ze słoniem i nieskończonością możemy używać podobnych metod.