W tym artykule opiszemy problem, który dotyczy tych właśnie brył, a został rozwiązany dopiero w lutym 2018 roku. Jego rozwiązanie opublikowano na łamach czasopisma American Mathematical Monthly.

Wyobraźmy sobie planetę będącą wielościanem foremnym. Na jednym z jej wierzchołków mieszka mysz, a w pozostałych wierzchołkach znajdują się pułapki na tę nieszczęsną mysz. Mysz chciałaby odbyć wędrówkę po tej planecie i bezpiecznie wrócić do domu. Ponieważ nie jest zbyt sprawna i nie potrafi zakręcać, może poruszać się wyłącznie prosto. Problem polega na stwierdzeniu, czy taka wędrówka bez natknięcia się na żadną z pułapek jest w ogóle możliwa na danym wielościanie.

Opiszemy bardziej formalnie wędrówkę myszy. Na zadanym wielościanie foremnym szukamy ścieżki, która spełnia następujące warunki:

• rozpoczyna się oraz kończy w ustalonym wierzchołku i nie przechodzi przez pozostałe wierzchołki;
• składa się z odcinków znajdujących się na ścianach wielościanu; w szczególności odcinki mogą się ze sobą przecinać;
• jeśli ścieżka przecina krawędź wielościanu ( "zmienia" ścianę na sąsiadującą), to odcinki wychodzący i wchodzący w tę krawędź leżą na wspólnej prostej, którą można narysować na pewnej siatce wielościanu.

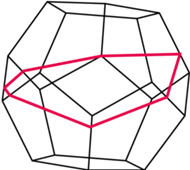
Ostatni punkt wyjaśnimy dokładnie na przykładzie sześcianu. Na rysunku poniżej z lewej strony czerwony odcinek spełnia wymagania stawiane w trzecim punkcie, gdyż na innej siatce tego samego sześcianu - środkowej na poniższym rysunku - oba odcinki leżą na jednej prostej.

Od dawna wiadomo, że taka ścieżka (trasa myszy) nie istnieje na czworościanie, sześcianie, ośmiościanie i dwudziestościanie. Problem jej istnienia pozostawał jednak otwarty dla dwunastościanu i rozwiązany został dopiero dwa lata temu. Rozwiązanie wygląda zdumiewająco prosto. Aż dziw bierze, że nikt wcześniej tego nie zauważył!

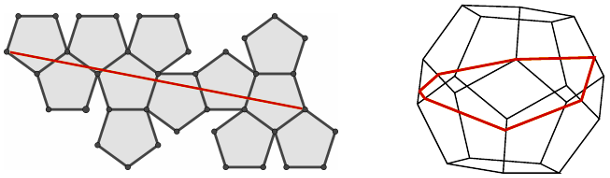
W dalszej części artykułu wrócimy do tego, co było wiadome już wcześniej - do nieistnienia ścieżki na innych bryłach. Wykażemy, że taka ścieżka nie istnieje na czworościanie. Rozumowanie będzie opierać się na sieci siatek połączonych ze sobą w uporządkowany sposób, jak na rysunku poniżej z lewej strony. Pojedyncza siatka wyznaczona jest przez trzy czarne wierzchołki (patrz wyróżniony trójkąt). Ponadto wyróżnione zostały pozostałe wierzchołki na czerwono lub biało, zgodnie ze schematem kolorowania na rysunku poniżej.

Wyjaśnimy teraz, jak należy rozumieć sieć siatek. Opiszemy, w jaki sposób "zwinąć" sieć siatek w zwykłą siatkę czworościanu (tę zaznaczoną na szaro), a następnie w czworościan. Zaletą korzystania z sieci siatek jest to, że wszystkie proste ścieżki na takiej sieci spełniają automatycznie warunek trzeci. Najpierw pokażemy, że faktycznie tak jest. Oznaczać to będzie, że zamiast poszukiwać ścieżki na czworościanie, możemy szukać prostego odcinka na sieci siatek, pomiędzy dwoma czarnymi wierzchołkami, który nie przechodzi przez żaden inny wierzchołek (ścieżki pokazane powyżej z prawej strony nie spełniają tego warunku).

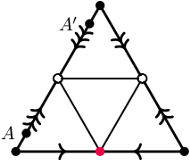
Zanim jednak zaczniemy zwijać, spójrzmy jeszcze na rysunek na marginesie. Przedstawia on siatkę czworościanu, na której wyróżnione zostały krawędzie, które zostaną ze sobą sklejone przy składaniu siatki (mają tyle samo strzałek). Sklejenie oznacza m.in., że punkt 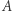zostanie połączony z punktem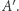

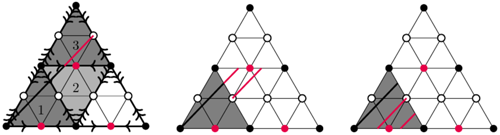
Wracamy teraz do zwijania sieci siatek na przykładzie konkretnej ścieżki (patrz rysunek poniżej z lewej strony). Ścieżka znajduje się między czarnym a białym punktem i przecina trzy wyróżnione siatki, oznaczone kolejno numerami 1, 2, 3.

Siatki składamy tak, aby dopasować do siebie kolorami wierzchołki oraz strzałki. Aby dopasować strzałki trzeciego i drugiego trójkąta, ten pierwszy należy obrócić dookoła różowego punktu z jego podstawy o 180 stopni. Podobnie dopasowujemy drugą do pierwszej. Dlaczego właśnie tak to robimy? Zauważmy, że siatkę drugiego trójkąta możemy narysować tak, że jego prawy górny trójkąt znajdzie się w miejscu lewego dolnego trójkąta trzeciej siatki (otrzymamy wtedy inną i poprawną siatkę - patrz rysunki siatek sześcianu). Tym samym reguła ta podpowiada nam, które trójkąty w siatkach 2 i 3 są identyczne oraz jak należy rozmieścić strzałki.

Na pierwszym rysunku czerwonym kolorem został zaznaczony fragment ścieżki, który przenosimy zgodnie z opisanymi wcześniej regułami na drugi trójkąt (środkowy rysunek). Następnie dwa czerwone odcinki (dłuższy z poprzedniego kroku i krótszy) z drugiego trójkąta (środkowy rysunek) przenosimy do szarego, otrzymując ścieżkę zawartą wyłącznie w szarym trójkącie (trzeci rysunek).

Rysunek na marginesie poniżej przedstawia tę samą ścieżkę narysowaną na czworościanie (widok z góry). Na stronie www.geogebra.org/m/j7pnmvxv można zobaczyć powyższą ścieżkę w trzech wymiarach.

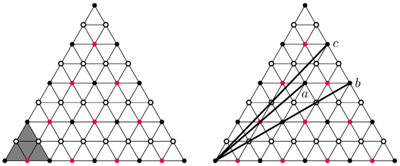
Wróćmy jeszcze na chwilę do trzech wyróżnionych wcześniej ścieżek na dużej sieci siatek. Dzięki opisanej tu metodzie zwijania łatwo możemy się przekonać, że ścieżka oznaczona literą to w istocie dwie kopie tej samej ścieżki, którą szczegółowo omawialiśmy powyżej. Tym samym nie ma potrzeby rozważania całej ścieżki - wystarczy jej fragment do pierwszego różowego lub białego wierzchołka. Wykażemy teraz, że na czworościanie nie da się narysować ścieżki o żądanych własnościach. Ustalmy, że ścieżka rozpoczyna się w górnym wierzchołku czworościanu, który na siatce reprezentowany jest przez czarny punkt w lewym dolnym rogu (a na sieci przez... wszystkie czarne punkty!).

Wiemy już, że prosta ścieżka na siatce siatek to trasa myszy, która spełnia nasze wymagania. Wiemy także, jak jednoznacznie składać siatkę siatek. Oznacza to, że każda ścieżka na siatce siatek ma jednoznaczną trasę na czworościanie. Zauważmy jednak, że rysując ścieżkę na siatce siatek łączącą czarne wierzchołki, zawsze przetniemy różowy lub biały wierzchołek (por. rysunek z trzema ścieżkami wyróżnionymi literami 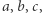str. 3)! Dowiedliśmy tym samym, że każda ścieżka rozpoczynająca się i kończąca w czarnym wierzchołku musi przeciąć inny wierzchołek czworościanu.

Przypadek czworościanu jest najprostszy ze wszystkich wielościanów foremnych. Pozostałe bryły również rozważa się przy użyciu sieci siatek, jednak te są znacznie bardziej skomplikowane. Niemniej wiemy już, że dwunastościan jest wyjątkowy wśród wszystkich brył platońskich.