Deltoid
Kroimy kostkę
Podzielmy kostkę na 27 przystających sześcianów (jak w kostce Rubika), a następnie wyrzućmy 7 z nich: ten ze środka oraz środkowy na każdej ze ścian. W kolejnych krokach konstrukcji powtarzajmy powyższą operację dla każdego z pozostających mniejszych sześcianów.
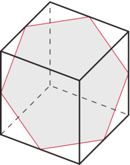
Rys. 1 Sześciokątny przekrój sześcianu
Po nieskończenie wielu takich krokach otrzymalibyśmy kostkę Mengera - fraktal o zerowej objętości, nieskończonej powierzchni i innych ciekawych własnościach. Zatrzymajmy się jednak po czwartym kroku konstrukcji.
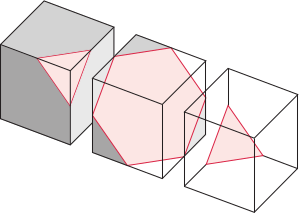
Sześcian można przeciąć płaszczyzną prostopadłą do głównej przekątnej i przechodzącą przez środki niektórych jego krawędzi, w przekroju uzyskując sześciokąt foremny (Rys. 1, oznaczmy płaszczyznę cięcia przez 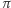 ).
).

(Wikimedia Commons, autor: Cmglee)
Rys. 3
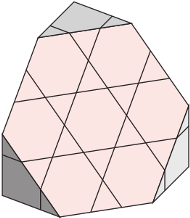
Jaki jest kształt i układ dziur na takim sześciokątnym przekroju czwartego kroku konstrukcji kostki Mengera?
Odpowiedź widać na rysunku 3 Uzasadnimy dwoma sposobami, że w pierwszym kroku konstrukcji na środku przekroju otrzymujemy dziurę w kształcie gwiazdki.
Sposób I. Przekrójmy płaszczyzną 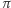 (jak na rysunku 1) cały sześcian podzielony na 27 mniejszych kostek. Zarówno środkowa kostka, jak i kostki przy środkach krawędzi, przez które przechodzi płaszczyzna
(jak na rysunku 1) cały sześcian podzielony na 27 mniejszych kostek. Zarówno środkowa kostka, jak i kostki przy środkach krawędzi, przez które przechodzi płaszczyzna 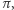 przecięte są w taki sam sposób jak całość, w przekroju uzyskujemy więc siedem odpowiednio mniejszych sześciokątów foremnych (Rys. 4).
przecięte są w taki sam sposób jak całość, w przekroju uzyskujemy więc siedem odpowiednio mniejszych sześciokątów foremnych (Rys. 4).
Płaszczyzna 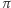 przecina też 12 innych małych kostek, przechodząc w każdej z nich przez środki trzech krawędzi o wspólnym wierzchołku. Takie przekroje są trójkątami równobocznymi (Rys. 5).
przecina też 12 innych małych kostek, przechodząc w każdej z nich przez środki trzech krawędzi o wspólnym wierzchołku. Takie przekroje są trójkątami równobocznymi (Rys. 5).
Sześciany usunięte w pierwszym kroku konstrukcji kostki Mengera składają się na sześciokąt na środku przekroju i sześć przylegających do niego trójkątów, co w sumie daje właśnie sześcioramienną gwiazdkę. W kolejnym kroku konstrukcji analogiczne mniejsze gwiazdki wycinane są z pozostałych sześciu sześciokątów z przekroju z rysunku 4, co tłumaczy także układ dziur widocznych na rysunku 3
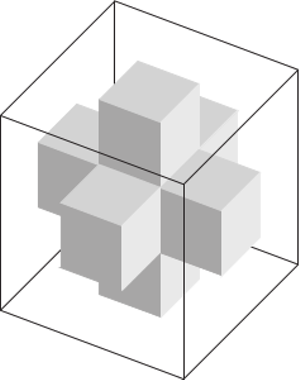
Sposób II. Pierwszy krok konstrukcji kostki Mengera można inaczej opisać jako wydrążenie w sześcianie trzech tuneli wyznaczonych przez kwadraty na środkach przeciwległych ścian (Rys. 6).
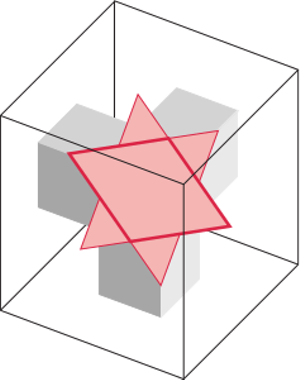
Przekrój płaszczyzną 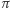 każdego z tych tuneli to romb o kątach
każdego z tych tuneli to romb o kątach 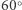 i
i 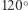 (na Rys. 5 na taki romb składają się dwa trójkąty i sześciokąt). Środkowa dziura-gwiazdka z rysunku 3 powstaje z trzech takich rombów (Rys. 7).
(na Rys. 5 na taki romb składają się dwa trójkąty i sześciokąt). Środkowa dziura-gwiazdka z rysunku 3 powstaje z trzech takich rombów (Rys. 7).