Jeśli kartkę z widocznym obok rysunkiem zegniemy wzdłuż poziomej prostej, to zobaczymy dwa wzajemnie wpisane czworościany - ten z kolorowymi wierzchołkami i ten z szarymi. Sprawdźmy to.

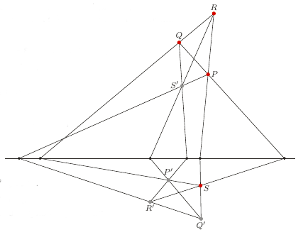
To, że 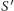leży na płaszczyźnie 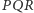jest oczywiste - są na tej samej części kartki.

To, że 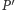leży na płaszczyźnie 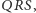wynika z przecinania się prostych 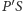i 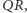bowiem przecinające się proste leżą na jednej płaszczyźnie, zresztą tak samo jest z prostymi równoległymi.

Ten sam argument uzasadnia, że 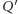leży na płaszczyźnie 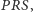a 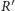na płaszczyźnie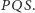

Tak więc czworościan 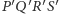jest wpisany w czworościan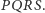

Analogicznie uzasadniamy wpisanie 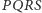w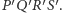

Wypada też zauważyć, że w rysunku, którego użyliśmy,
nie ma nic nadzwyczajnego - każdy może bez trudu wykonać podobny.