Stożki i walce
Od Archimedesa wiemy, że zdaniem Demokryta stożek stanowi trzecią część walca, ale pierwszy udowodnił to Eudoksos. Znamy ten rezultat z XII Księgi Elementów Euklidesa (Stwierdzenie 10)...
Euklides, korzystając z metody wyczerpywania (wyjmując graniastosłupy o znanej objętości), pokazał, że ostrosłup o podstawie trójkątnej ma objętość, którą wyraża wzór
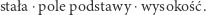 |
(*) |
Stałą wyznaczył z obserwacji: ostrosłup stanowi trzecią część opisanego na nim graniastosłupa (Rys. 1). Może Euklides chciał w ten sposób uniknąć korzystania z przejść granicznych przy wyznaczaniu stałej we wzorze 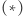 lub potwierdzić jej wartość na innej drodze? Następnie, przybliżając stożek ostrosłupami, uzasadnił twierdzenie Eudoksosa.
lub potwierdzić jej wartość na innej drodze? Następnie, przybliżając stożek ostrosłupami, uzasadnił twierdzenie Eudoksosa.

Rys. 1
Czy we wzorze na objętość stożka, który również jest postaci 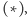 można potwierdzić wartość stałej bez ponownego odwoływania się do przejść granicznych? W Elementach takiej informacji nie ma. My pokażemy, że jest to możliwe. Wykorzystamy pomysły Archimedesa sprzed 2200 lat.
można potwierdzić wartość stałej bez ponownego odwoływania się do przejść granicznych? W Elementach takiej informacji nie ma. My pokażemy, że jest to możliwe. Wykorzystamy pomysły Archimedesa sprzed 2200 lat.
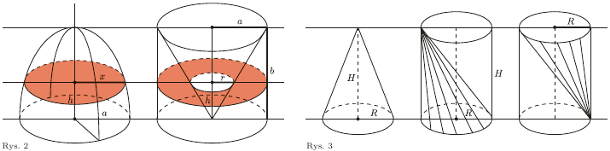
Gdy weźmiemy elipsę o półosiach  i obrócimy ją wokół pionowej osi
i obrócimy ją wokół pionowej osi 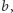 to otrzymamy bryłę - elipsoidę obrotową. Rozważmy z jednej strony górną połowę takiej elipsoidy opartą na kole o promieniu
to otrzymamy bryłę - elipsoidę obrotową. Rozważmy z jednej strony górną połowę takiej elipsoidy opartą na kole o promieniu 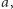 zaś z drugiej strony walec o wysokości
zaś z drugiej strony walec o wysokości 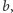 którego podstawą jest koło o promieniu
którego podstawą jest koło o promieniu 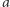 (Rys. 2).
(Rys. 2).
Archimedes zauważył, że jeśli z tego walca wytniemy stożek i obie bryły przetniemy wspólną płaszczyzną równoległą do podstawy na wysokości 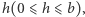 to pola otrzymanych przekrojów zawsze będą równe. Dla elipsoidy,
to pola otrzymanych przekrojów zawsze będą równe. Dla elipsoidy, 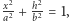 więc
więc 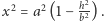 Zatem pole przekroju elipsoidy jest równe
Zatem pole przekroju elipsoidy jest równe 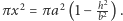 Ponieważ dla drugiej figury
Ponieważ dla drugiej figury 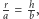 więc
więc 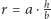 i pole pierścienia jest równe
i pole pierścienia jest równe 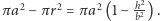 Zatem objętość połowy elipsoidy obrotowej jest równa objętości opisanego na niej walca pomniejszonej o objętość wydrążonego w nim stożka. Warto również zaznaczyć, że gdy
Zatem objętość połowy elipsoidy obrotowej jest równa objętości opisanego na niej walca pomniejszonej o objętość wydrążonego w nim stożka. Warto również zaznaczyć, że gdy  to z tych rozważań wynika wzór na objętość kuli:
to z tych rozważań wynika wzór na objętość kuli: 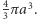
Rys. 4
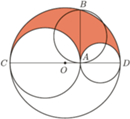
Rozważmy teraz walec o wysokości 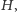 którego podstawą jest koło o promieniu
którego podstawą jest koło o promieniu 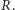 Objętość tego walca jest równa
Objętość tego walca jest równa 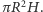 W tym walcu umieszczamy dwa stożki, każdy o wysokości
W tym walcu umieszczamy dwa stożki, każdy o wysokości 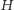 i podstawach będących podstawami walca (Rys. 3).
i podstawach będących podstawami walca (Rys. 3).
Stożki te mają taką samą objętość. Nie wypełniają one objętości walca. Gdy taki walec przetniemy na wysokości 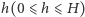 płaszczyzną równoległą do jego podstaw, to naszym oczom ukaże się widok przedstawiony na rysunku 4. Kolorowy obszar
płaszczyzną równoległą do jego podstaw, to naszym oczom ukaże się widok przedstawiony na rysunku 4. Kolorowy obszar 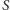 ma pole równe polu koła o średnicy
ma pole równe polu koła o średnicy 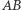 (to również wiedział Archimedes):
(to również wiedział Archimedes):

Pole to jest największe (równe 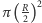 ), gdy przecięcie jest w połowie wysokości walca i maleje, gdy cięcia przesuwają się w górę albo w dół. Oznacza to, że czwarta część objętości walca leżąca poza stożkami może być przedstawiona jako połowa elipsoidy obrotowej o wysokości
), gdy przecięcie jest w połowie wysokości walca i maleje, gdy cięcia przesuwają się w górę albo w dół. Oznacza to, że czwarta część objętości walca leżąca poza stożkami może być przedstawiona jako połowa elipsoidy obrotowej o wysokości 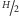 mającej w podstawie koło o promieniu
mającej w podstawie koło o promieniu 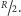 Aby się o tym przekonać, wystarczy wyznaczyć zależność długości odcinka
Aby się o tym przekonać, wystarczy wyznaczyć zależność długości odcinka  od odległości między płaszczyzną tnącą a płaszczyzną połowiącą walec. Można również przekształcić odcinek
od odległości między płaszczyzną tnącą a płaszczyzną połowiącą walec. Można również przekształcić odcinek 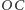 na odcinek o długości
na odcinek o długości 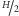 przez powinowactwo prostokątne. Takie przekształcenie łuk okręgu przeprowadza w łuk elipsy. Dzięki temu otrzymujemy "równanie objętości brył":
przez powinowactwo prostokątne. Takie przekształcenie łuk okręgu przeprowadza w łuk elipsy. Dzięki temu otrzymujemy "równanie objętości brył":

gdzie 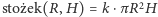 i niewiadomą jest
i niewiadomą jest 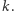 Przekształcając powyższe równanie do postaci
Przekształcając powyższe równanie do postaci

otrzymujemy 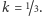 Mamy więc potwierdzenie, że stożek o wysokości
Mamy więc potwierdzenie, że stożek o wysokości 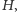 mający w podstawie koło o promieniu
mający w podstawie koło o promieniu  ma objętość równą
ma objętość równą 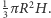
Spróbujemy teraz wyznaczyć objętość paraboloidy obrotowej o wysokości  i promieniu podstawy
i promieniu podstawy  Oczywiście, nie chcemy używać rachunku całkowego. Równanie paraboli tworzącej paraboloidę obrotową o promieniu podstawy
Oczywiście, nie chcemy używać rachunku całkowego. Równanie paraboli tworzącej paraboloidę obrotową o promieniu podstawy 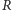 i wysokości
i wysokości 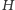 jest następujące:
jest następujące: 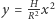 (Rys. 5; taka parabola jest jedyna!). Obok rozważmy walec o wysokości
(Rys. 5; taka parabola jest jedyna!). Obok rozważmy walec o wysokości 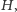 którego podstawą jest koło o promieniu
którego podstawą jest koło o promieniu 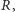 w którym wydrążono paraboloidę obrotową utworzoną przez parabolę
w którym wydrążono paraboloidę obrotową utworzoną przez parabolę  W wyniku przecięcia obu brył na wysokości
W wyniku przecięcia obu brył na wysokości 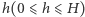 płaszczyzną równoległą do podstawy otrzymujemy koło o polu
płaszczyzną równoległą do podstawy otrzymujemy koło o polu 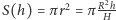 (korzystamy z równania paraboli
(korzystamy z równania paraboli 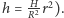
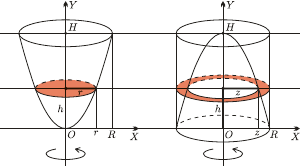
Rys. 5
Ponieważ dla pierścienia mamy 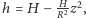 więc
więc

Oznacza to, że objętość paraboloidy obrotowej jest równa połowie objętości opisanego na niej walca: 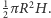
Miłośnikom rachunków polecam inne rozwiązanie: można bez trudu sprawdzić, że na rysunku 6 kolorowe obszary obrócone wokół osi 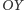 wyznaczają w przestrzeni bryły o równych objętościach.
wyznaczają w przestrzeni bryły o równych objętościach.
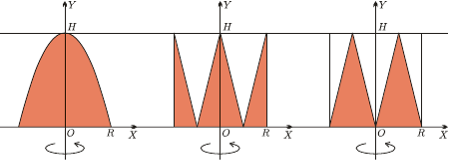
Rys. 6
Ciekawe, czy Euklides byłby zadowolony z takiego rozwiązania...