Czy Ziemia jest płaska? A może jednak?
W artykule Czy Ziemia jest płaska (Delta 4/2016) pokazaliśmy, że sfera (będąca uproszczonym modelem powierzchni Ziemi) nie jest płaska, to znaczy nie daje się podzielić na fragmenty, z których każdy byłby izometryczny z pewnym fragmentem płaszczyzny. Przypomnijmy, że ta cecha odróżnia sferę od powierzchni bocznych walca i stożka. Pójdźmy więc dalej - czy jest możliwa taka gładka deformacja sfery, aby uzyskać powierzchnię płaską?

Rys. 1
Pytanie jest o tyle zasadne, że sama Ziemia nie ma kształtu idealnej kuli, tylko elipsoidy obrotowej, a i to tylko w przybliżeniu. Rysunek 1 pokazuje przykład gładkiej deformacji, w efekcie której otrzymujemy sześcian z wygładzonymi kantami. Istotnie, jego ściany są fragmentami płaszczyzny, a w okolicach krawędzi można wykorzystać fragmenty powierzchni walca. Jedyne niepłaskie części są w okolicach wierzchołków, ale może i tego da się uniknąć?
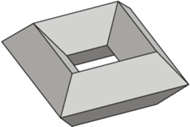
Rys. 2
Pokażemy, że taka deformacja nie jest możliwa. Aby to wykazać, wykorzystamy niezmiennik zwany charakterystyką Eulera. Można już było o nim przeczytać w artykule Wzór Eulera i balony (Delta 9/2005) oraz w Deltoidzie 3/2016. Przypomnijmy najpierw twierdzenie Eulera: dla dowolnego wielościanu wypukłego zachodzi wzór
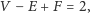 |
gdzie 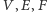 to odpowiednio liczba jego wierzchołków, krawędzi i ścian. Oczywiście, wzór ten pozostanie słuszny, jeśli wielościan "nadmuchamy" w taki sposób, by jego powierzchnia miała kształt sfery. Charakterystyka Eulera sfery to po prostu liczba
to odpowiednio liczba jego wierzchołków, krawędzi i ścian. Oczywiście, wzór ten pozostanie słuszny, jeśli wielościan "nadmuchamy" w taki sposób, by jego powierzchnia miała kształt sfery. Charakterystyka Eulera sfery to po prostu liczba 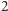 pojawiająca się po prawej stronie przedstawionej równości. Dlaczego nazwaliśmy ją niezmiennikiem? Otóż jeśli będziemy rozważać wielościany na zdeformowanej sferze (na przykład tej z rysunku 1), wzór Eulera pozostanie w mocy. Jest tak, gdyż deformacja sfery wraz z rozrysowanym na niej wielościanem nie zmienia liczby jego wierzchołków, krawędzi i ścian. Obserwacja wydaje się błaha, ale odnotujmy, że dla wielościanów na torusie (powierzchni dętki) otrzymujemy inny wynik:
pojawiająca się po prawej stronie przedstawionej równości. Dlaczego nazwaliśmy ją niezmiennikiem? Otóż jeśli będziemy rozważać wielościany na zdeformowanej sferze (na przykład tej z rysunku 1), wzór Eulera pozostanie w mocy. Jest tak, gdyż deformacja sfery wraz z rozrysowanym na niej wielościanem nie zmienia liczby jego wierzchołków, krawędzi i ścian. Obserwacja wydaje się błaha, ale odnotujmy, że dla wielościanów na torusie (powierzchni dętki) otrzymujemy inny wynik: 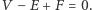 Czytelnik może to sprawdzić na rysunku 2 Podobnie jak dla sfery, otrzymana liczba 0 nie zależy od wyboru wielościanu. W ten sposób przekonujemy się, że sfera i torus mają różne charakterystyki Eulera, w konsekwencji nie da się otrzymać jednej z tych powierzchni przez deformację drugiej.
Czytelnik może to sprawdzić na rysunku 2 Podobnie jak dla sfery, otrzymana liczba 0 nie zależy od wyboru wielościanu. W ten sposób przekonujemy się, że sfera i torus mają różne charakterystyki Eulera, w konsekwencji nie da się otrzymać jednej z tych powierzchni przez deformację drugiej.
Przypuśćmy więc przeciwnie, że zdeformowana w pewien sposób sfera jest płaska; dla przejrzystości ilustracje będą przedstawiały sferę bez deformacji, ale nie zmniejsza to ogólności rozważań. Płaskość oznacza, że każdy punkt ma otoczenie izometryczne z fragmentem płaszczyzny; każde takie otoczenie nazwiemy płatem. Do pokrycia całej sfery można wybrać pewną skończoną liczbę płatów, a następnie skupić uwagę jedynie na tej kolekcji (na przykład powierzchnię boczną walca da się pokryć dwoma płatami). Mapą nazwiemy izometrię przekształcającą płat we fragment płaszczyzny, a także obraz tej izometrii - w przypadku powierzchni Ziemi to pojęcie jest zbliżone do tego, co zwykliśmy oglądać w atlasach.
Skonstruujemy teraz wielościan spełniający poniższe trzy warunki:
- (1)
- Wszystkie ściany są trójkątami (mają po trzy krzywoliniowe boki).
- (2)
- Każdy z tych trójkątów zawiera się w pewnym płacie, a więc jest izometryczny z pewną figurą na płaszczyźnie.
- (3)
- Tak otrzymana figura na płaszczyźnie jest trójkątem prostoliniowym, czyli jej boki są odcinkami.
Warunek 1 jest bardzo łatwo spełnić, na przykład rysując na sferze ośmiościan foremny (powstaje on przez trzy prostopadłe cięcia). Dla spełnienia warunku 2 rysunek ten, być może, trzeba "zagęścić". W tym celu wybierzmy jedną ze ścian ośmiościanu i zrzutujmy ją na płaszczyznę tak, aby otrzymać trójkąt prostoliniowy (na przykład, stosując rzut środkowy). W otrzymanym trójkącie narysujmy środkowe, dzieląc go na sześć mniejszych trójkątów (nazywamy to podziałem barycentrycznym). Z każdym z powstałych trójkątów możemy zrobić to samo, i tak dalej wybraną liczbę razy. Następnie otrzymaną siatkę umieśćmy z powrotem na sferze. Przypomnijmy, że jest ona pokryta przez pewną liczbę płatów; jeśli podział będzie dostatecznie drobny (czyli podziału barycentrycznego dokonamy dostatecznie wiele razy), każdy z drobnych trójkącików będzie się mieścił w którymś z płatów.

Rys. 3
Na potrzeby ostatniego z warunków pozostaje "wyprostować krawędzie". Wybierzmy dowolną krawędź; leży ona w jednym z płatów i w odpowiedniej mapie jest pewną krzywą łączącą obrazy wierzchołków. Wystarczy zastąpić tę krzywą przez odcinek łączący te same punkty. Czytelnik Czujny może tutaj zrobić zastrzeżenie: wybrana krawędź potencjalnie leży w więcej niż jednym płacie, więc mogłoby się okazać, że krawędź wyprostowana w jednej mapie okaże się krzywa w innej. Tak jednak nie jest - uzasadnienie opiera się na stwierdzeniu, że złożenie dwóch izometrii jest izometrią, a izometrie płaszczyzny przekształcają odcinki na odcinki.
Dla tak skonstruowanego wielościanu obliczymy teraz charakterystykę Eulera. Zbadajmy w tym celu sumę wszystkich kątów wewnętrznych w ścianach - rozumiemy przez to, oczywiście, kąty w trójkątach prostoliniowych powstałych po zmapowaniu ścian. Suma kątów przy każdym wierzchołku to 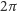 , a więc razem otrzymujemy
, a więc razem otrzymujemy 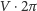 . Z drugiej strony, suma kątów wewnętrznych każdego z trójkątów wynosi
. Z drugiej strony, suma kątów wewnętrznych każdego z trójkątów wynosi  (to właśnie tutaj korzystamy z założenia płaskości!), więc łącznie dostajemy
(to właśnie tutaj korzystamy z założenia płaskości!), więc łącznie dostajemy 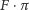 . Z przyrównania tych dwóch wielkości wynika równość
. Z przyrównania tych dwóch wielkości wynika równość 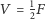 . Jeśli ponadto weźmiemy pod uwagę, że każda ściana ma trzy krawędzie, a każda krawędź rozdziela dwie ściany, to otrzymamy
. Jeśli ponadto weźmiemy pod uwagę, że każda ściana ma trzy krawędzie, a każda krawędź rozdziela dwie ściany, to otrzymamy 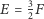 . W rezultacie obliczamy charakterystykę Eulera
. W rezultacie obliczamy charakterystykę Eulera

Otrzymana sprzeczność z twierdzeniem Eulera dowodzi, że nawet zdeformowana sfera nie może być płaska.
Rys. 4
Jeśli przeanalizować powyższy dowód dokładniej, to okaże się, że każda płaska powierzchnia zamknięta ma charakterystykę Eulera równą zeru. Przez powierzchnię zamkniętą rozumiemy ograniczoną (a więc nie płaszczyznę) i bez brzegu (co wyklucza powierzchnię boczną walca). Zamiast sfery możemy więc z tym samym skutkiem rozważać dwuprecel (o charakterystyce 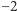 ) lub inny wieloprecel (charakterystyka precla o
) lub inny wieloprecel (charakterystyka precla o 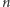 dziurach to
dziurach to 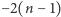 ), ale już nie torus. Rzeczywiście, charakterystyka Eulera torusa wynosi
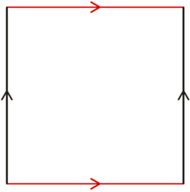
), ale już nie torus. Rzeczywiście, charakterystyka Eulera torusa wynosi 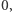 a więc nasze rozumowanie nie prowadzi do sprzeczności. To nie jest przypadek! Jeśli Czytelnik konstruował kiedyś torus z kartki papieru poprzez sklejenie odpowiednich boków (jak na rysunku 4), to zauważył, że o ile jedną parę boków można skleić bez trudu, to sklejenie drugiej bez załamania kartki jest już niemożliwe. Okazuje się, że w przestrzeni czterowymiarowej kartkę da się zgiąć i skleić, otrzymując w ten sposób płaski torus, ale to zupełnie inna historia...
a więc nasze rozumowanie nie prowadzi do sprzeczności. To nie jest przypadek! Jeśli Czytelnik konstruował kiedyś torus z kartki papieru poprzez sklejenie odpowiednich boków (jak na rysunku 4), to zauważył, że o ile jedną parę boków można skleić bez trudu, to sklejenie drugiej bez załamania kartki jest już niemożliwe. Okazuje się, że w przestrzeni czterowymiarowej kartkę da się zgiąć i skleić, otrzymując w ten sposób płaski torus, ale to zupełnie inna historia...