Drobiazgi
Brzydka prawda
Wielościan wypukły, którego ściany są jednakowymi wielokątami foremnymi, może mieć ściany trójkątne, czworokątne lub pięciokątne. Ostatnie dwa przypadki realizują się tylko w postaci sześcianu i dwunastościanu...
Pozostałe trzy wielościany foremne reprezentują pierwszy przypadek (czworościan, ośmiościan i dwudziestościan), ale nie są one jedynymi wielościanami wypukłymi, których ściany są trójkątami równobocznymi - np. "górna" i "dolna" piątka ścian dwudziestościanu składa się na dziesięciościan przypominający dysk.
Oznaczmy przez 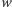 liczbę wszystkich wierzchołków wielościanu,
liczbę wszystkich wierzchołków wielościanu, 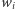 - liczbę tych wierzchołków, w których zbiega się
- liczbę tych wierzchołków, w których zbiega się 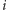 ścian (oczywiście
ścian (oczywiście 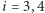 lub
lub 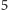 ), przez
), przez 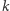 liczbę krawędzi i przez
liczbę krawędzi i przez  liczbę ścian.
liczbę ścian.
Aby znaleźć wszystkie takie wielościany, można rozumować tak:

bo każda ściana ma trzy krawędzie, a każda krawędź należy do dwóch ścian, a także łączy dwa wierzchołki. Ponieważ na dodatek 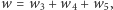 więc wstawiając to do wzoru Eulera:
więc wstawiając to do wzoru Eulera: 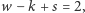 dla wygody pomnożonego przez 6, otrzymujemy
dla wygody pomnożonego przez 6, otrzymujemy

czyli

To równanie ma 19 rozwiązań w liczbach naturalnych: 4,0,0 ; 3,1,1; 3,0,3; 2,3,0 ; 2,2,2; 2,1,4; 2,0,6; 1,4,1; 1,3,3; 1,2,5; 1,1,7; 1,0,9; 0,6,0 ; 0,5,2 ; 0,4,4 ; 0,3,6 ; 0,2,8 ; 0,1,10; 0,0,12 .
Niestety, tylko osiem z nich (zaznaczone są kolorem) odpowiada wielościanowi wypukłemu (te grubszą czcionką to foremne).
I tu jest miejsce na zwrot brzydka prawda: fakt ten nosi dumną nazwę twierdzenie Freudenthala-van der Waerdena, ale mimo naturalnej materii, jakiej dotyczy, nie ma dotąd naturalnego i eleganckiego dowodu.
Więc może któryś z Czytelników?