Mała Delta
Sferostożki więcej i bardziej

Gwoli precyzji ustalmy, że trzymając przed sobą zetknięte połówki przeciętej bryły obrotowej (prawą i lewą), obracamy prawą z nich ruchem do siebie.
Taka sobie niewinnie wyglądająca bryłka. Ot, powstała z obrotu kwadratu dookoła jego przekątnej, przecięcia tego, co powstało, na dwie identyczne części (wzdłuż płaszczyzny kwadratu), przekręceniu połowy o 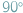 i doklejeniu do drugiej części (czekającej w tym czasie w bezruchu). Szczęśliwa całość - sferostożek (ang. sphericon).
i doklejeniu do drugiej części (czekającej w tym czasie w bezruchu). Szczęśliwa całość - sferostożek (ang. sphericon).
To tylko wierzchołek góry lodowej, jeden z przedstawicieli licznej rodziny, której członkowie powstają przez podmianę kwadratu (w pierwszym etapie produkcji) na inne figury foremne - przekątną zastępujemy osią symetrii przechodzącą przez wierzchołek. W ten sposób otrzymujemy nowe cudaczne dziwolągi (rodzinne zdjęcie poniżej), których przedstawicieli nazywamy 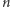 -sferostożkami 1, gdzie
-sferostożkami 1, gdzie 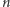 jest liczbą kątów wejściowego wielokąta foremnego (o jedynce za moment).
jest liczbą kątów wejściowego wielokąta foremnego (o jedynce za moment).
Powyższe bryły to kolejno (od lewej) 5-, 6-, 7-, 10-sferostożek 1. Po rozcięciu bryły obrotowej połówka jest przekręcana o kąt 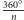 - w ten sposób części zawsze do siebie pasują. Każdy z tych sferostożków toczy się po pochylonym blacie (czasem z niewielką pomocą ludzkich mięśni) w dość spektakularny sposób - jak na możliwe do uzyskania efekty toczącej się bryły. Spróbuj znaleźć, Drogi Czytelniku, właściciela poniższego śladu.
- w ten sposób części zawsze do siebie pasują. Każdy z tych sferostożków toczy się po pochylonym blacie (czasem z niewielką pomocą ludzkich mięśni) w dość spektakularny sposób - jak na możliwe do uzyskania efekty toczącej się bryły. Spróbuj znaleźć, Drogi Czytelniku, właściciela poniższego śladu.

Opisane dotychczas twory to nie wszystko z tego gatunku. Z pewnością sam widzisz pole do tworzenia nowych stworzeń. Po przekrojeniu bryły obrotowej, powstałej przez obracanie wielokąta foremnego wokół osi symetrii, połowę możemy obracać o dowolną wielokrotność 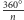 - otrzymując w tenże sposób
- otrzymując w tenże sposób 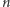 -sferostożki
-sferostożki 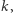 gdzie
gdzie 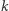 oznacza obrót połowy o kąt
oznacza obrót połowy o kąt 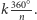 Sferostożki mogą powstać z dowolnego wielokąta foremnego, można badać ich krawędzie, ściany i ślady. Na marginesie znajdziesz 30-sferostożek 3 z wyróżnioną ścianą, po której bryła może się toczyć bez końca.
Sferostożki mogą powstać z dowolnego wielokąta foremnego, można badać ich krawędzie, ściany i ślady. Na marginesie znajdziesz 30-sferostożek 3 z wyróżnioną ścianą, po której bryła może się toczyć bez końca.
Wiesz już sporo, ale to ciągle nie koniec  Wielokąt foremny obracać można wokół osi symetrii nieprzechodzącej przez wierzchołek figury (co jest możliwe dla parzystych
Wielokąt foremny obracać można wokół osi symetrii nieprzechodzącej przez wierzchołek figury (co jest możliwe dla parzystych 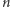 ). Nie zmieniając dalszych etapów tworzenia, uzyskamy
). Nie zmieniając dalszych etapów tworzenia, uzyskamy 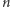 -sferostożki
-sferostożki 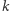 dualne.
dualne.
Wiesz wystarczająco dużo, żeby zmierzyć się z poniższymi pytaniami.
ROZGRZEWKA
1. Ile ścian ma 4-sferostożek 1? Ile krawędzi ma 4-sferostożek dualny?
2. Ile ścian ma 3-sferostożek?
3. Jaka jest zależność między liczbą ścian i krawędzi sferostożka (dualnego bądź nie) od 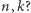
4. Ślady jakich sferostożków (dualnych bądź nie) mają proste fragmenty (przykładem jest ślad powyżej)?
5. Jakie pary 8-sferostożków 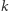 będą zostawiały ślady, będące lustrzanymi odbiciami?
będą zostawiały ślady, będące lustrzanymi odbiciami?
Zanim przejdziesz do ostatecznego wyzwania, zapoznaj się z techniką analizowania pewnych własności sferostożków. Dla przykładu rozważmy 5-sferostożek 1. Bryła obrotowa powstała z obrotu pięciokąta ma trzy ściany. Wytęż na moment wyobraźnię i ponumeruj odpowiednio krawędzie pięciokąta. Krawędzie oznaczone tymi samymi numerami leżą na tej samej ścianie. Druga połowa jest obrócona o kąt 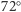 - numeracja pięciokąta została zmieniona. Po połączeniu części (lewej z niezmienioną numeracją i prawej obróconej) odpowiednie wierzchołki i krawędzie sferostożka zostaną sklejone. W obrębie jednej połowy dwie krawędzie z tym samym numerem są połączone ścianą, natomiast odpowiednie sklejenie wierzchołków z różnych połówek zostało przedstawione na rysunku za pomocą dodatkowych linii.
- numeracja pięciokąta została zmieniona. Po połączeniu części (lewej z niezmienioną numeracją i prawej obróconej) odpowiednie wierzchołki i krawędzie sferostożka zostaną sklejone. W obrębie jednej połowy dwie krawędzie z tym samym numerem są połączone ścianą, natomiast odpowiednie sklejenie wierzchołków z różnych połówek zostało przedstawione na rysunku za pomocą dodatkowych linii.

Teraz, nawet bez modelu sferostożka w dłoniach, można opisać zachowanie toczącej się bryły. Zacznijmy od krawędzi z numerem 3 na prawej połowie. Krawędź ta jest połączona z krawędzią 2 lewej połowy. Druga krawędź 2 lewej połowy jest połączona z krawędzią 1 prawej połowy. Druga krawędź 1 prawej połowy jest połączona z krawędzią 1 lewej połowy. Druga krawędź 1 lewej połowy jest połączona z krawędzią 2 prawej połowy. Druga krawędź 2 prawej połowy jest połączona z krawędzią 3 lewej połowy i na tym koniec. Krawędź 3 z lewej połowy nie jest połączona z żadną inną krawędzią na tej połowie, sferostożek przestaje się toczyć po pochylonym blacie. Ten nieco mglisty opis można zapisać prościej

Wytłuszczoną czcionką zaznaczone są krawędzie wielokąta dla prawej połowy. Oznacza to, że sferostożek ma jedną ścianę (właśnie się po niej przetoczył), jednak nie może toczyć się bez końca (ile w takim razie ma krawędzi?).
Czas na WYZWANIE
6. Gdy sferostożek ma tylko jedną ścianę, można pokusić się o pewne malowanki i pociągnąć linię wzdłuż środka jego ściany. Kiedy linia ta będzie pętlą?
7. Czy możliwe jest zatoczenie pętli przy rysowaniu kreski wzdłuż środka ściany sferostożka, gdy nie jest to jedyna jego ściana (jest to możliwe, na przykład, na ścianie bocznej walca)?
8. Czy ślad sferostożka może być pętlą? To znaczy, czy tocząc się bez poślizgu i bez cofania (w intuicyjnym tego słowa znaczeniu) sferostożek może znaleźć się w miejscu i pozycji, w których zaczął toczenie?
9. Czy ślad sferostożka może przecinać sam siebie?
10. Jakie sferostożki mają ślad środkowosymetryczny?
Po wykonaniu powyższych ćwiczeń (albo chociaż ich części) jesteś gotowy do dalszych badań. Cóż, dlaczegóż by nie skrzyżować sferostożków dualnych i niedualnych? Jeżeli oba powstały z obrotu tej samej figury foremnej, to po przekrojeniu brył na połowy części będą do siebie pasować. Takie twory nazwiemy 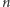 -sferostożkami
-sferostożkami 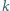 półdualnymi. W tym przypadku również można pokusić się o znalezienie zależności między wyjściową figurą foremną a liczbą krawędzi, wierzchołków czy ścian, można analizować, kiedy takie bryły mogą toczyć się bez końca. Wszelkie opisy dotyczące własności tych brył będą dla świata nowe, więc tym bardziej zachęcamy do badań (sami chętnie co nieco się dowiemy)!
półdualnymi. W tym przypadku również można pokusić się o znalezienie zależności między wyjściową figurą foremną a liczbą krawędzi, wierzchołków czy ścian, można analizować, kiedy takie bryły mogą toczyć się bez końca. Wszelkie opisy dotyczące własności tych brył będą dla świata nowe, więc tym bardziej zachęcamy do badań (sami chętnie co nieco się dowiemy)!
A czy to koniec? Ależ nie... Niektóre figury nieforemne również będą miały tę własność, że tworząc z nich bryłę obrotową, można przekroić ją na dwie pasujące do siebie części. Ale to kolejna historia...
Na zakończenie
Animacja Sferostożek powstała za pomocą linuxowego programu poturlaj Przemysława Kiciaka. Program ten, będący częścią pakietu BSTools, służy do rysowania i animowania sferostożków opisanych w artykule. Animacje sferostożków są dostępne na naszym kanale w serwisie YouTube.









 -sferostożki półdualne, doświadczasz wiekopomnej chwili. Z prawdopodobieństwem bliskim jedności czytasz bowiem pierwszą wzmiankę o tego typu bryłach, która pojawiła się we wszechświecie. A w każdym razie mimo wielu starań nic na ten temat w ziemskiej literaturze autorom znaleźć się nie udało. Jeżeli jednak natrafisz na jakiś ślad, czym prędzej poinformuj o tym Redakcję!
-sferostożki półdualne, doświadczasz wiekopomnej chwili. Z prawdopodobieństwem bliskim jedności czytasz bowiem pierwszą wzmiankę o tego typu bryłach, która pojawiła się we wszechświecie. A w każdym razie mimo wielu starań nic na ten temat w ziemskiej literaturze autorom znaleźć się nie udało. Jeżeli jednak natrafisz na jakiś ślad, czym prędzej poinformuj o tym Redakcję!

