Jakich wielościanów nie ma, a jakie są?
Kubuś Fatalista, bohater książki Denisa Diderota, spotkał pewnego razu rozpaczliwie płaczące dziecko. Na pytanie, co mu się stało, odpowiedziało, że kazano mu powiedzieć A. Cóż w tym złego? - dopytywał się Kubuś. - Bo jak powiem A, to każą mi powiedzieć B - poskarżył się malec.
Ludzie są jednak optymistami i pół wieku temu mówiliby raczej o tym, że gdy wejdzie się na kilka szczebli drabiny, to ma się ogromną ochotę wchodzić dalej. A dziś zapewne byłoby o tym, że gdy zaliczy się pewien poziom gry komputerowej, to przechodzi się do następnego.

Diagramy Schlegela wielościanów foremnych
Tu będziemy się jednak trzymać wersji Diderota.
A. Wykazać, że nie ma wielościanu o siedmiu krawędziach.
Jeśli wielościan ma choć jedną ścianę czworokątną, to ma co najmniej osiem krawędzi, bo z każdego wierzchołka tego czworokąta wychodzą co najmniej trzy krawędzie, z czego dwie do sąsiednich wierzchołków. Jeszcze więcej "przymusowych" krawędzi będzie, gdy któraś ze ścian będzie miała więcej niż 4 boki. Zostały nam wielościany o wszystkich ścianach trójkątnych. Jeśli tych ścian jest 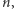 to krawędzi jest
to krawędzi jest 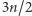 (bo każda łączy dwie ściany), a taka liczba nie chce być równa 7.
(bo każda łączy dwie ściany), a taka liczba nie chce być równa 7.
B. Istnieje wielościan o 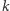 krawędziach dla każdego
krawędziach dla każdego 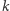 większego od
większego od 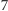 i dla
i dla 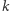 równego
równego 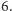
Dla 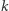 parzystych taki jest np. ostrosłup o podstawie
parzystych taki jest np. ostrosłup o podstawie 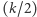 -kątnej. Jeśli natomiast obetniemy troszkę jeden z wierzchołków przy podstawie, to liczba krawędzi zwiększy się o 3, a więc otrzymamy wszystkie liczby nieparzyste, poczynając od 9.
-kątnej. Jeśli natomiast obetniemy troszkę jeden z wierzchołków przy podstawie, to liczba krawędzi zwiększy się o 3, a więc otrzymamy wszystkie liczby nieparzyste, poczynając od 9.
C. Jakie są jeszcze ograniczenia na liczbę 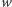 - wierzchołków,
- wierzchołków,  - ścian i
- ścian i 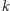 - krawędzi?
- krawędzi?
Ponieważ dowolne trzy punkty leżą na jakiejś płaszczyźnie, więc 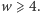 Ale wówczas również
Ale wówczas również 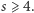 O liczbie
O liczbie 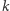 już było. Liczby te są związane jeszcze zależnościami
już było. Liczby te są związane jeszcze zależnościami 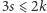 i
i 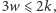 bo każda krawędź należy do dwóch ścian, a ściany te są co najmniej trójkątne; podobnie każda krawędź łączy dwa wierzchołki, a z każdego z nich wychodzi ich co najmniej trzy.
bo każda krawędź należy do dwóch ścian, a ściany te są co najmniej trójkątne; podobnie każda krawędź łączy dwa wierzchołki, a z każdego z nich wychodzi ich co najmniej trzy.
D. Czy istnieje tylko jeden wielościan o danych 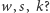
Oczywiście nie. Na przykład sześcian i czworościan z dwoma obciętymi rogami mają te same 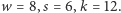
E. Dalej będziemy zajmowali się wielościanami wypukłymi. Wielościan taki można określić w ten sposób, że gdyby dowolna z jego ścian była przezroczysta, to można byłoby tak zbliżyć do niej oko, że przez nią widziałoby się wszystkie inne ściany. Taki widok nazywa się diagramem Schlegela.
Skoro literą jest E, to teraz wzór Eulera: 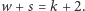
Korzystając z diagramu Schlegela, wzór ten uzasadnić nietrudno. Na początek uznajmy to, co leży dokoła diagramu, też za jego ścianę - trzeba tak zrobić, by diagram miał tyle ścian, co wielościan, z którego powstał. A teraz będziemy usuwali z niego krawędzie i wierzchołki, przestrzegając tego, by nie podzielić diagramu na rozłączne części: stale powinno być możliwe dotarcie po nieusuniętych jeszcze krawędziach do każdego z nieusuniętych dotąd wierzchołków.
A sposoby są dwa:
- 1.
- gdy po obu stronach krawędzi są różne ściany (na początku w diagramie każda z krawędzi ma tę własność) - usuwamy ją, zostawiając kończące ją wierzchołki;
- 2.
- gdy krawędź kończy się wierzchołkiem, z którego nie wychodzi prócz niej żadna inna krawędź - usuwamy ją wraz z tym wierzchołkiem.
Przypadek pierwszy zmniejsza o jeden liczbę krawędzi i liczbę ścian. Przypadek drugi - o jeden liczbę krawędzi i liczbę wierzchołków. Zatem w obu przypadkach odejmujemy po jedynce od obu stron wzoru Eulera.
A ponieważ w ten sposób możemy po kolei usunąć wszystkie krawędzie (sprawdźcie!), więc na końcu zostanie nam jeden wierzchołek i "otaczająca go" ściana. A ponieważ 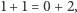 więc wzór Eulera został udowodniony.
więc wzór Eulera został udowodniony.

Można za jego pomocą oszacować liczbę ścian i wierzchołków z drugiej strony. W C stwierdziliśmy, że 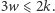 Wstawiając to do wzoru Eulera, otrzymujemy
Wstawiając to do wzoru Eulera, otrzymujemy 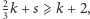 czyli
czyli 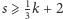 ; podobnie
; podobnie 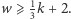
F. Przy odcinaniu wierzchołków, w których zbiegają się 3 krawędzie (robiliśmy to już parę razy) - nazwijmy to operacją OD - liczba krawędzi rośnie o 3, liczba wierzchołków o 2 (bo 3 przybyły, a jeden ubył) i liczba ścian o 1.
Przeciwna operacja: dobudowywanie na trójkątnej ścianie ostrosłupa (uzasadnij, że można to zrobić, nie psując wypukłości!) - operacja DO - zwiększa liczbę krawędzi o 3, liczbę wierzchołków o 1 i liczbę ścian o 2 (znów 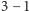 ).
).
Do wielościanu mającego  wierzchołków,
wierzchołków,  ścian i
ścian i 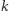 krawędzi udało się zastosować
krawędzi udało się zastosować 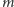 operacji OD i
operacji OD i  operacji DO. Ile teraz ma on wierzchołków, ścian i krawędzi?
operacji DO. Ile teraz ma on wierzchołków, ścian i krawędzi?
Prosty rachunek daje 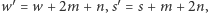
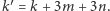
G. (twierdzenie Steinitza) Jeśli liczby 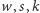 spełniają warunki
spełniają warunki 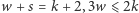 i
i 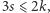 to istnieje wielościan mający
to istnieje wielościan mający 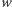 wierzchołków,
wierzchołków,  ścian i
ścian i 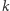 krawędzi.
krawędzi.
Dla dowodu wygodnie będzie przyjąć, że 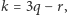 gdzie
gdzie  to 0, 1 lub 2. Z nierówności uzyskanych na koniec E mamy
to 0, 1 lub 2. Z nierówności uzyskanych na koniec E mamy 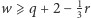 i
i 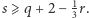 Zatem (ponieważ
Zatem (ponieważ 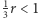 ) mamy
) mamy 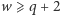 i
i 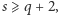 z czego wynika, że liczby
z czego wynika, że liczby 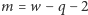 i
i  są nieujemne i nadają się na krotności operacji OD i DO.
są nieujemne i nadają się na krotności operacji OD i DO.
Inaczej: 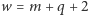 i
i 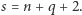 Z wzoru Eulera mamy więc
Z wzoru Eulera mamy więc 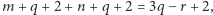 czyli
czyli 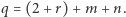 Podstawiając to zamiast
Podstawiając to zamiast 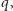 otrzymujemy
otrzymujemy

Stąd twierdzenie będzie dowiedzione, gdy wskażemy wielościan, w którym 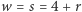 i
i 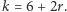 Ale taki jest ostrosłup o podstawie trój-, czworo- lub pięciokątnej. Są w każdym z nich ściany trójkątne (to te boczne) i wierzchołki trójścienne (przy podstawie), więc można stosować OD i DO.
Ale taki jest ostrosłup o podstawie trój-, czworo- lub pięciokątnej. Są w każdym z nich ściany trójkątne (to te boczne) i wierzchołki trójścienne (przy podstawie), więc można stosować OD i DO.
H. Warunkiem koniecznym i dostatecznym na to, by istniał wielościan mający 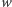 wierzchołków i
wierzchołków i  ścian, są nierówności
ścian, są nierówności 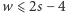 i
i 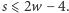
Oczywiście, należy to twierdzenie sprowadzić do poprzedniego, a w tym celu wystarczy porachować, że - gdy jest spełniony wzór Eulera - nierówności z C są równoważne nierównościom w sformułowaniu tego twierdzenia.
I. I co dalej? Dalsze litery alfabetu trzeba już sobie samemu wymyślić. Na przykład może to być próba znalezienia odpowiedzi na pytanie, jak - znając spełniające podane tu nierówności liczby 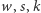 - obliczyć, ile jest różnych wielościanów (to znaczy mających różne zestawy ścian) o
- obliczyć, ile jest różnych wielościanów (to znaczy mających różne zestawy ścian) o 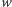 wierzchołkach,
wierzchołkach,  ścianach i
ścianach i 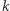 krawędziach. Dla 4, 4, 6 jest jeden, dla 8, 6, 12 - jak to już sprawdziliśmy - co najmniej dwa, a jak jest "w ogóle"?
krawędziach. Dla 4, 4, 6 jest jeden, dla 8, 6, 12 - jak to już sprawdziliśmy - co najmniej dwa, a jak jest "w ogóle"?
To świetny temat na samodzielną pracę (a gdy ktoś jest uczniem - na nasz Konkurs Uczniowskich Prac z Matematyki).