Deltoid
Panaceum?
W rozwiązaniach wielu zadań kluczowe jest rozłożenie danej bryły tak, by uzyskać jej siatkę. Jeśli z kolei chcemy zbudować model wielościanu, często rysujemy jego siatkę, wycinamy, składamy... Siatki to przydatne narzędzie, jednakże - jak to z narzędziami bywa - trzeba ostrożnie się nimi posługiwać. Proszę ocenić poprawność poniższych trzech stwierdzeń.
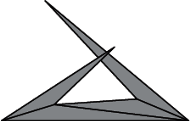
Rys. 1
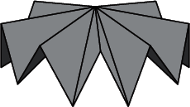
Rys. 2
To nie koniec kłopotów z siatkami. Jeśli model wielościanu rozcinamy wzdłuż pewnych krawędzi, by uzyskać jego siatkę, może nas spotkać niespodzianka przedstawiona na rysunku 1 - siatka nachodzi sama na siebie! Nie da się jej narysować na kartce, wyciąć i złożyć. Ale łatwo ją poprawić: odciąć lewą ścianę i przykleić wzdłuż którejś z jej pozostałych krawędzi.
Czy zawsze, gdy otrzymamy siatkę, która sama na siebie nachodzi, istnieje inna siatka, pozbawiona tej wady?
Rysunek 2 przedstawia powierzchnię z brzegiem. Rozcięcie jednej krawędzi pozwala ją "rozpłaszczyć", ale nachodzi wtedy sama na siebie, gdyż suma kątów płaskich przy jej centralnym wierzchołku przekracza 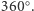 Rozcięcie drugiej krawędzi sprawia, że powierzchnia rozpada się na dwie części. Nie istnieje więc żadna jej siatka, która nie nachodziłaby sama na siebie.
Rozcięcie drugiej krawędzi sprawia, że powierzchnia rozpada się na dwie części. Nie istnieje więc żadna jej siatka, która nie nachodziłaby sama na siebie.
Istnieją również wielościany o tej własności. Wszystkie znane przykłady są wklęsłe. Nie wiadomo, czy istnieje taki wielościan wypukły - problem ten, zwany hipotezą Shepharda, jest (o ile wiem) otwarty.