Jak opisać kryształ?

Katarzyna Wyrobek
Gips
Kryształy to jedne z najbardziej osobliwych elementów świata przyrody. Materiały krystaliczne wykazują niemal niespotykaną naturalną tendencję do tworzenia wielościanów. Piętnastometrowe kryształy w Meksyku czy dwumilimetrowe kryształki soli w naszej kuchni - wszystkie swą szczególną postać zawdzięczają uporządkowanemu rozmieszczeniu atomów, jonów lub cząsteczek.
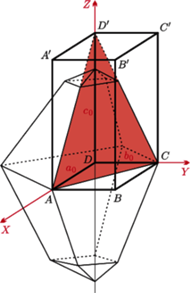
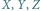 - osie krystalograficzne,
- osie krystalograficzne,
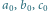 - jednostki osiowe,
- jednostki osiowe,
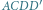 - czworościan zasadniczy,
- czworościan zasadniczy,
 - komórka elementarna (równoległościan).
- komórka elementarna (równoległościan).
Krystalografia, czyli nauka o wewnętrznej i zewnętrznej budowie oraz fizycznych i fizykochemicznych właściwościach ciał krystalicznych, zawiera wiele mniejszych działów badających przeróżne cechy kryształów z wykorzystaniem zaawansowanych technik współczesnej nauki. A cóż my, prości zjadacze chleba, o nieuzbrojonym oku, jesteśmy w stanie powiedzieć o "kamyku" przywiezionym jako pamiątka z kopalni? Gdy chodzi o monokryształ, możemy dokonać prawie pełnego opisu jego struktury zewnętrznej, tym samym zamieniając się w początkujących znawców krystalografii strukturalnej.
Na przełomie lat 1890 i 1891 Artur Schönflies i Jewgraf Fiodorow, analizując budowę zewnętrzną i wewnętrzną kryształów, niezależnie stwierdzili, że istnieje 230 możliwych krystalograficznych grup przestrzennych (czyli sposobów rytmicznego wypełnienia przestrzeni przez jednakowe monokryształy) oraz że istnieją 32 klasy krystalograficznych monokryształów (dwa monokryształy należą do tej samej klasy, gdy mają takie same izometrie własne, czyli przekształcenia, które nakładają je same na siebie).
Jak możemy sklasyfikować nasz kryształ? Umieśćmy go w przestrzennym układzie współrzędnych tworzonym zwykle przez trzy osie krystalograficzne, w sposób przedstawiony na rysunku obok.
Przystępujemy do badania. Pierwszym krokiem będzie określenie rodziny, do której należy nasz kryształ. Czym jest rodzina krystalograficzna? Jest to zbiór ciał krystalicznych o takim samym czworościanie zasadniczym. Na kształt czworościanu wpływają długości jednostek osiowych i miary kątów między osiami. Istnieje sześć różnych rodzin krystalograficznych:
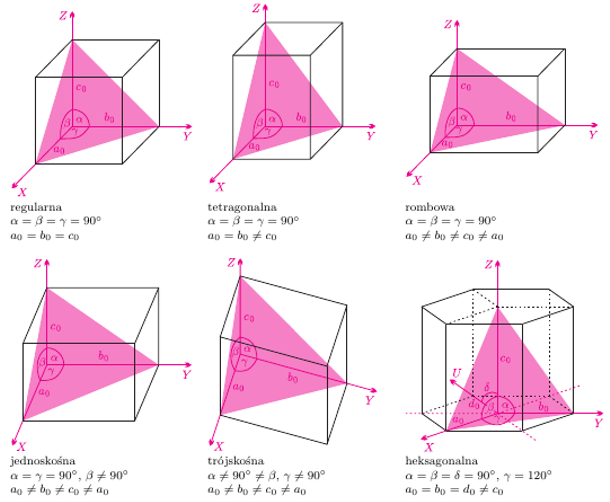
Kolejnym etapem jest wybór układu krystalograficznego. Układy krystalograficzne zostały wyróżnione ze względu na kształt komórki elementarnej. Każdej z rodzin odpowiada jeden rodzaj komórki elementarnej (zaznaczone na rysunkach), a więc jeden analogiczny rodzaj układu. Wyjątkiem jest rodzina heksagonalna, dla której możliwe są aż dwie kombinacje: układ heksagonalny i układ trygonalny (patrz rysunki na marginesie).
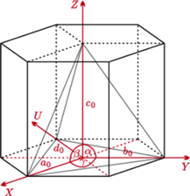
układ heksagonalny
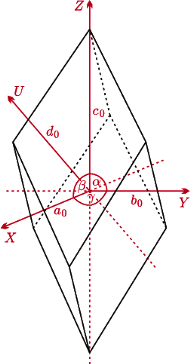
układ trygonalny
Który wybrać w naszym przypadku? Układ heksagonalny cechuje się 6-krotną osią symetrii, trygonalny zaś jedynie 3-krotną. Wybieramy tę odpowiadającą naszemu kryształowi i problem rozwiązany. Przykładowo kwarc (patrz tylna strona okładki) i kalcyt należą do rodziny heksagonalnej, układu trygonalnego.
Ostatnią czynnością w opisie struktury zewnętrznej kryształu jest dobór jednej z 32 klas krystalograficznych. Klasy krystalograficzne są przyporządkowaniem ze względu na symetrię bryły, zatem będziemy szczegółowo rozpatrywać makroskopowe elementy symetrii naszego kryształu, a więc osie symetrii, osie inwersyjne, środek symetrii, płaszczyzny symetrii.
Dla jednego układu krystalograficznego występuje maksymalnie 7 klas, co ułatwi nam znalezienie tej właściwej. Abyśmy mogli lepiej zrozumieć ten problem, pokażę go na przykładzie. Rozpocznijmy analizę.
Podstawową sprawą jest dostrzeżenie osi symetrii, ich liczby i krotności. W krystalografii oznacza się je za pomocą 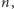 gdzie
gdzie 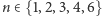 i wskazuje na ich krotność. Przy poszukiwaniu osi symetrii nie powinniśmy ograniczać się tylko do kierunków wyznaczanych przez osie krystalograficzne. Możemy znaleźć jedną, trzy lub nie dostrzec żadnej osi. W przypadku braku osi symetrii bryła może mieć oś inwersyjną - inwersją nazywane jest tu złożenie obrotu względem osi z symetrią względem leżącego na niej punktu, w tym przypadku środka symetrii komórki. Osie inwersyjne oznacza się symbolami
i wskazuje na ich krotność. Przy poszukiwaniu osi symetrii nie powinniśmy ograniczać się tylko do kierunków wyznaczanych przez osie krystalograficzne. Możemy znaleźć jedną, trzy lub nie dostrzec żadnej osi. W przypadku braku osi symetrii bryła może mieć oś inwersyjną - inwersją nazywane jest tu złożenie obrotu względem osi z symetrią względem leżącego na niej punktu, w tym przypadku środka symetrii komórki. Osie inwersyjne oznacza się symbolami 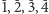 lub
lub 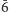 w zależności od ich krotności. Przykładem minerału z rodziny jednoskośnej o jednokrotnej osi inwersyjnej jest gips.
w zależności od ich krotności. Przykładem minerału z rodziny jednoskośnej o jednokrotnej osi inwersyjnej jest gips.
Jeżeli bryła ma jedną oś symetrii, może też mieć środek symetrii. Dla osi nieparzystokrotnych równoznaczne jest to z przekształceniem osi inwersyjnej, dlatego nie wyróżnia się w tym przypadku nowych klas. Dla osi parzystokrotnych środek symetrii warunkuje występowanie płaszczyzny symetrii. Możliwa jest również sytuacja, kiedy kryształ nie ma środka symetrii, a mimo to ma płaszczyzny symetrii, w dodatku (z wyjątkiem klasy 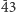 m) przecinające się wzdłuż jednej osi. Jest to warunkowane występowaniem dodatkowo dwóch inwersyjnych osi parzystokrotnych.
m) przecinające się wzdłuż jednej osi. Jest to warunkowane występowaniem dodatkowo dwóch inwersyjnych osi parzystokrotnych.

Tom Loomis
Beryl - zaznaczone osie symetrii
Jeżeli mamy do czynienia z trzema osiami symetrii, to dodatkowo dla poszczególnych układów wyznaczono miary kątów między nimi. Przykładowo heksagonalny kryształ berylu ma aż trzy osie symetrii: 6-krotną i dwie 2-krotne prostopadłe do niej i tworzące kąt 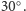 W przypadku trzech osi możliwe jest również istnienie środka symetrii na przecięciu tych osi i tak też jest w tej sytuacji. Sprawia to, że można zauważyć płaszczyzny prostopadłe do osi parzystokrotnych. Gdybyśmy w takich okolicznościach spotkali się z 3-krotną osią symetrii, to okazałoby się, że jest ona osią inwersyjną.
W przypadku trzech osi możliwe jest również istnienie środka symetrii na przecięciu tych osi i tak też jest w tej sytuacji. Sprawia to, że można zauważyć płaszczyzny prostopadłe do osi parzystokrotnych. Gdybyśmy w takich okolicznościach spotkali się z 3-krotną osią symetrii, to okazałoby się, że jest ona osią inwersyjną.
Wszystkie nasze poczynania zmierzają do zaklasyfikowania kryształu do jednej z 230 grup krystalograficznych. W tym momencie niezbędna jest już analiza struktury wewnętrznej, a tego tzw. gołym okiem nie zrobimy. Kierując się jednak słowami Alberta Einsteina "Spójrz głęboko w przyrodę, a wtedy wszystko lepiej zrozumiesz", zgłębiajmy niezgłębione, szukajmy inspiracji w otoczeniu i dajmy się czasem zaskoczyć.
Krystalografowie-matematycy zamiast komórkami elementarnymi wolą się zajmować grupami ich izometrii własnych (przez geologów i fizyków nazywanych symetriami). Takie grupy noszą nazwę skończonych grup punktowych. Napiszemy o nich w jednym następnych numerów.
Redakcja
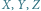 - osie krystalograficzne,
- osie krystalograficzne,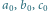 - jednostki osiowe,
- jednostki osiowe,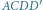 - czworościan zasadniczy,
- czworościan zasadniczy,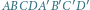 - komórka elementarna (równoległościan).
- komórka elementarna (równoległościan).