Rys. 1

Rys. 2

Rys. 3

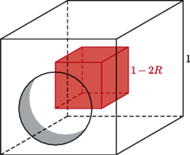
Aby odpowiedzieć na to pytanie, zbadajmy, gdzie leży w sześcianie środek zawartej w nim kulki o promieniu  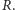 Odpowiedź jest na rysunku 1 – oczywiście, w odległości co najmniej 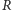  od ścian sześcianu, czyli w mniejszym sześcianiku o krawędzi 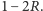 Oznaczmy tę liczbę przez 

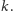
Nasze zadanie sprowadza się teraz do znalezienia takich trzech punktów w tym sześcianiku, aby najmniejsza z odległości między nimi (oznaczmy ją 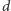 ) była jak największa – w nich umieścimy środki naszych kulek: ich promienie będą równe 

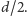
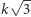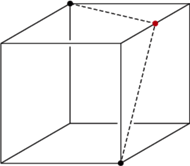
Pomysł, by zacząć od obrania dwóch najdalszych punktów w sześcianiku (czyli odległych o  ), daje nam  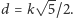Faktycznie (Rys. 2) kolorowy punkt ma taką odległość od obranych punktów czarnych, a jakiekolwiek jego poruszenie w sześcianiku zmniejsza jego odległość od jednego z nich.

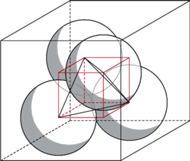
Rys. 4

Okazuje się, że ten wynik można poprawić, zaczynając „słabiej”, czyli nie od punktów położonych na końcach przekątnej sześcianiku, lecz na końcach przekątnej jego ściany. Takie punkty są odległe o 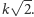  Jak łatwo spostrzec, każdy wierzchołek sześcianiku należy do trzech ścian, więc do wyboru na pozostałe dwa „stanowiska” najbardziej odległych punktów mamy punktów aż trzy. 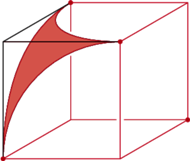Rysując sferę o środku w wierzchołku sześcianiku i promieniu  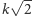(Rys. 3), bez trudu stwierdzamy, że poruszenie dowolnego z punktów spowoduje zmniejszenie jego odległości od co najmniej dwóch spośród pozostałych. Można więc jako środki trzech możliwie największych kulek w sześcianie jednostkowym wybrać dowolne trzy spośród tak wyróżnionych wierzchołków sześcianiku, bo nietrudno stwierdzić, że 

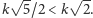
Mamy zresztą nie tylko położenie środków największych kulek, ale też i ich promienie, bo z 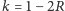  i 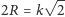  wynika 

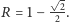
Patrząc na rysunek 3, widzimy też, że „niechcący” dowiedliśmy zdanie rozpoczynające ten tekst. Cztery kulki zostały sportretowane na rysunku 4. Oczywiście, mniejsze kulki też zmieszczą się w sześcianie.

Łatwo zauważyć tu pole do dalszych zadań. Można sprawdzić, że gdy w sześcianie mieści się jedna kulka, to nie zawsze da się włożyć tam jeszcze jedną taką samą, podobnie będzie dla dwóch – ale jak będzie dla pięciu, sześciu itd.? Wydaje mi się, że początkowe stwierdzenie będzie też prawdziwe dla czworościanu foremnego – ale czy to prawda? A czy dałoby się sformułować podobne (i prawdziwe) stwierdzenia dla innych wielościanów? 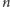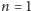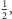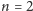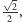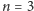No i można też zadać pytanie o maksymalny rozmiar  jednakowych kulek mieszczących się w jednostkowym sześcianie – dla   mamy   dla  jest to   dla (i 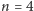 ) obliczyliśmy przed chwilą, dla 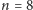 mamy 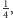  ale co dla innych