Drobiazgi
Piłka w puszce
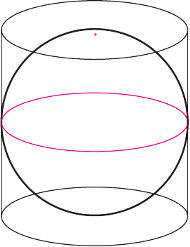
Piłki tenisowe na ogół pakowane są w rurkę po kilka sztuk. Wyobraźmy sobie piłki tak cenne, że pakowane są każda oddzielnie. Takie opakowanie to z matematycznego punktu widzenia walec...
Rys. 1
Rys. 2
Piłka styka się z jego powierzchnią boczną wzdłuż okręgu, a przekrój osiowy tego walca jest kwadratem (Rys. 1). Okazuje się, że tak zapuszkowana piłka ma powierzchnię równą powierzchni bocznej swojej puszki, czyli
Twierdzenie. Powierzchnia sfery jest równa powierzchni bocznej opisanego na niej walca.
Jeszcze ciekawszy od samego faktu jest jego starożytny dowód, pochodzący od Archimedesa. Zapoczątkował on bardzo popularny w matematycznej praktyce obyczaj, że gdy chcemy coś udowodnić, to dowodzimy czegoś zupełnie innego.
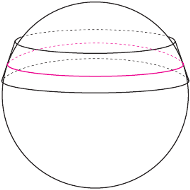
W tym przypadku udowodnimy, że jeśli wytniemy z piłki (czyli sfery) plasterek płaszczyznami równoległymi do denek puszki (czyli podstaw walca) i w połowie jego wysokości opiszemy na nim płaską obręcz (czyli stożek ścięty, Rys. 2), to jej powierzchnia będzie taka sama, jak powierzchnia wyciętego przez te płaszczyzny fragmentu puszki (czyli powierzchnia boczna walca, tylko tym razem niskiego). Nie narysowałem go, bo nic nie byłoby wtedy widać.
Ale gdy narysujemy przekrój opisanej sytuacji płaszczyzną przechodzącą przez
środek piłki i prostopadłą do denek puszki, to wszystko stanie się widoczne
(Rys. 3). Kolorowe kreski to fragment puszki (oznaczmy jego wysokość
przez
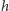 ) i fragment obręczy
) i fragment obręczy
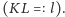 Narysujmy przez punkt
Narysujmy przez punkt
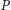 styczności obręczy i piłki odcinek
styczności obręczy i piłki odcinek
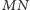 – przesunięty fragment
puszki oraz odcinek
– przesunięty fragment
puszki oraz odcinek
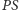 łączący
łączący
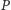 ze środkiem piłki i odcinek
ze środkiem piłki i odcinek
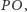 gdzie
gdzie
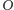 jest rzutem prostokątnym
jest rzutem prostokątnym
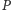 na oś symetrii
puszki.
na oś symetrii
puszki.
Ponieważ
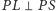 i
i
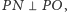 więc trójkąty
więc trójkąty
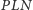 i
i
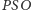 są podobne, co daje
są podobne, co daje

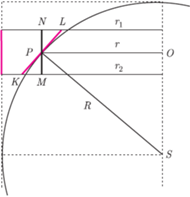
Rys. 3
Znane wzory na pole powierzchni bocznej walca i stożka ściętego przekonują nas, że dowiedliśmy tego, co chcieliśmy, ale jak to się ma do wyróżnionej kolorem prawidłowości?
Zauważmy, że gdy podzielimy piłkę i puszkę na plasterki, to suma pól obręczy
opisanych na plasterkach złoży się na całą powierzchnię boczną puszki, czyli
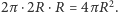 Dalej Archimedes pisze tak: gdy będziemy
rozpatrywali coraz węższe plasterki, to otrzymywane obręcze będą w sumie
coraz podobniejsze do powierzchni piłki, aż w końcu (my mówimy:
w granicy) będą z tą powierzchnią identyczne. A ponieważ dla każdego
podziału suma powierzchni obręczy będzie równa powierzchni bocznej puszki,
więc tak będzie i na końcu.
Dalej Archimedes pisze tak: gdy będziemy
rozpatrywali coraz węższe plasterki, to otrzymywane obręcze będą w sumie
coraz podobniejsze do powierzchni piłki, aż w końcu (my mówimy:
w granicy) będą z tą powierzchnią identyczne. A ponieważ dla każdego
podziału suma powierzchni obręczy będzie równa powierzchni bocznej puszki,
więc tak będzie i na końcu.
Czy zgodzilibyśmy się na takie rozumowanie?