Mała Delta
Mądra linka?
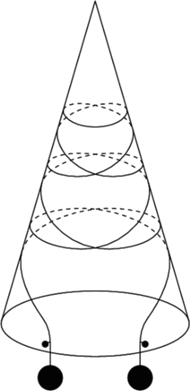
Rys. 1
Na bardzo śliski plastikowy stożek (można takie nabyć w sklepach z pomocami szkolnymi) nawijamy kilka zwojów nylonowej cieniutkiej linki (plecionej, aby była giętka) i obciążamy jej końce ciężarkami, a także nie pozwalamy lince odwinąć się (np. przyklejając blisko podstawy stożka wystające sztyfty – Rys. 1).
Powiadają, że taki przyrząd pozwala stwierdzić, iż owa linka ma swój rozum, a przynajmniej własny pogląd na to, ile co najwyżej jej zwojów powinno być na stożku. Pogląd ten demonstruje jakoby, gdy spokojnie, ale zdecydowanie potrząsamy stożkiem (trzymając go, oczywiście, cały czas wierzchołkiem do góry). Podobno, gdy linka uważa, że zwojów jest za wiele, podsuwa się do góry, zrzucając kolejne pętle przez wierzchołek. A że to czynność rozumna, ma nas przekonać obserwacja, iż przestaje figlować zawsze przy tej samej liczbie zwojów na stożku.
Oczywiście, umysł prymitywny postarałby się o stożek, linkę i sprawdził, czy tak jest w istocie (chyba teraz mówi się – w realu). Ale my postąpimy, jak potępiani dziś uczeni średniowieczni, pogardliwie zwani scholastykami. Owi scholastycy, podobno, nawet liczbę zębów u konia ustalali rozumowaniem, nie poniżając się do pospolitego zajrzenia mu w zęby. Zastanówmy się zatem teoretycznie i my, dlaczego mianowicie linka mogłaby tak czynić, jak głosi fama.
Jako punkt startu rozważań przyjmiemy za wiadome, że naciągana (u nas przez obciążniki) linka stara się być możliwie najprostsza, czyli łączyć punkty możliwie najkrótszymi swymi odcinkami, a raczej kawałkami, bo na stożku to, rzecz jasna, odcinki mogą być tylko wtedy, gdy linka przechodziłaby przez wierzchołek.
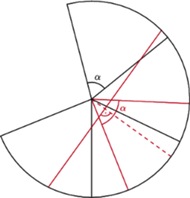
Rys. 2
Ten ślad prowadzi od razu do tego, by stożek (intelektualnie oczywiście)
rozciąć i położyć na płaszczyźnie – będzie to wycinek koła (oznaczmy jego
kąt przez
 ). W tej sytuacji napięta na stożku linka będzie wyglądała jak
odcinek.
). W tej sytuacji napięta na stożku linka będzie wyglądała jak
odcinek.
Aby tę myśl doprecyzować, zamiast rozcinać stożek zrobiony z jednej warstwy papieru, lepiej wyobrazić sobie, że jest on sporą liczbę razy zwiniętą kartką papieru, tak jak nieraz robi się stożkowe torebki na popcorn. Korzyść będzie taka, że wówczas wielokrotnie otaczającą stożek (napiętą) linkę będzie można narysować w jednym kawałku (Rys. 2) – będzie to faktycznie odcinek.
Wykorzystajmy ten obrazek jeszcze i w ten sposób, aby spośród wszelkich możliwych rozcięć stożka wybrać to, które będzie najbardziej korzystne dla dalszych rozważań – będzie to rozcięcie, którego dwusieczna przechodzi przez najbliższy wierzchołkowi punkt linki.

Rys. 3
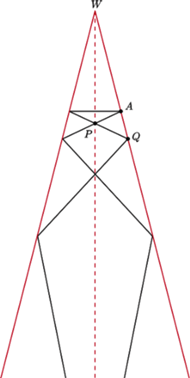
Rys. 4
Taki wybór rozcięcia stożka pozwoli nam wygodnie przenieść rozważania ze stożka „wielowarstwowego” na stożek „jednowarstwowy”. A taka operacja jest niezbędna, gdyż na „wielowarstwowym” nie widać pętli.
Wygodę zapewnia fakt, że punkty
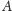 i
i
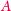 z rysunku 3 to po
zwinięciu jeden punkt. Rysunek pokazuje ponadto, gdzie po zwinięciu znajdzie
się punkt
z rysunku 3 to po
zwinięciu jeden punkt. Rysunek pokazuje ponadto, gdzie po zwinięciu znajdzie
się punkt
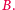 Tym, co będzie dla nas najważniejsze, jest stwierdzenie, że
kąty, jakie z krawędzią rozcięcia tworzą odcinki
Tym, co będzie dla nas najważniejsze, jest stwierdzenie, że
kąty, jakie z krawędzią rozcięcia tworzą odcinki
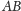 i
i
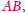 są
równe.
są
równe.
Jeśli stożek został zwinięty z wycinka koła o rozwartości
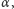 to kąt
to kąt
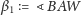 będzie równy
będzie równy
 Zatem kąt pierwszego
samoprzecięcia linki będzie równy
Zatem kąt pierwszego
samoprzecięcia linki będzie równy
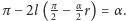
Oznaczmy przez
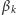 kąt, pod jakim linka
kąt, pod jakim linka
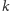 -ty raz przecina linię
rozcięcia lub dwusieczną wycinka. Bez trudu, korzystając z twierdzenia o kącie
zewnętrznym, stwierdzamy, że
-ty raz przecina linię
rozcięcia lub dwusieczną wycinka. Bez trudu, korzystając z twierdzenia o kącie
zewnętrznym, stwierdzamy, że
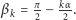 Istotnie (Rys. 4):
Istotnie (Rys. 4):

i konsekwentnie
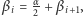 a to przez indukcję daje nam właśnie
podany wyżej warunek na
a to przez indukcję daje nam właśnie
podany wyżej warunek na
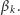
Skoro tak, to
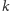 -te samoprzecięcie linki będzie pod kątem
-te samoprzecięcie linki będzie pod kątem

Tu wypada po raz pierwszy zastanowić się nad tym, czy przypadkiem nasza scholastyczna matematyka nie oderwała się zanadto od rzeczywistości. Chwila refleksji i uzupełniamy nasze rozumowanie o zastrzeżenie:
oczywiście, gdy takie przecięcie będzie istniało.
Nietrudno bowiem zauważyć, że liczba
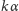 niezależnie od
tego, ile wynosi
niezależnie od
tego, ile wynosi
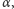 dla odpowiednio dużych
dla odpowiednio dużych
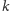 przekroczy
przekroczy
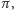 a wtedy nasze rozważania tracą sens. Zatem, aby istniało
a wtedy nasze rozważania tracą sens. Zatem, aby istniało
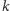 -te
samoprzecięcie, musi być spełniona nierówność
-te
samoprzecięcie, musi być spełniona nierówność
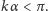
Otrzymaliśmy zatem
Wniosek. linka
na stożku powstałym z wycinka koła o rozwartości
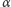 będzie miała
dokładnie
będzie miała
dokładnie
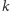 samoprzecięć (czyli będzie się składała z
samoprzecięć (czyli będzie się składała z
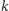 pętli),
gdy spełniony będzie warunek
pętli),
gdy spełniony będzie warunek
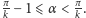
Można to przeliczyć na kąt
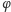 między tworzącymi stożka a jego
osią. Nie wątpię, że Czytelnik Skrupulatny bez większego trudu ustali, że
zależność ta to
między tworzącymi stożka a jego
osią. Nie wątpię, że Czytelnik Skrupulatny bez większego trudu ustali, że
zależność ta to
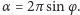 Wynika z tego, na przykład, że stożek,
którego przekrój osiowy jest trójkątem równobocznym, nie powinien
tolerować na sobie ani jednej pętli. Te powinny w stabilny sposób istnieć
tylko na węższych stożkach.
Wynika z tego, na przykład, że stożek,
którego przekrój osiowy jest trójkątem równobocznym, nie powinien
tolerować na sobie ani jednej pętli. Te powinny w stabilny sposób istnieć
tylko na węższych stożkach.

Gdy już raz dopuściliśmy wątpliwość, czy formalnie prowadzone rachunki muszą mieć odpowiednik w realnym świecie, to zadajmy teraz pytanie: co się stanie, gdy wykonamy opisane na wstępie doświadczenie, na początek nawijając na stożek więcej pętli, niż wynikło z naszych obliczeń? Czy faktycznie pętle będą się posuwały do góry, by zeskoczyć przez wierzchołek? Gdyby tak miało być, to jakie warunki musiałby spełniać, np. współczynnik tarcia linki o stożek? Bo przecież nie ulega wątpliwości, że napinana linka będzie „chciała” przybrać obliczone przez nas położenie, czyli kształt lokalnie najkrótszy.
A pytań może być więcej. Na przykład, co zrobi linka, gdy pętli nawiniemy mniej, niż to wynika z rachunku? Zaplącze się sama bardziej? Albo: jak by przebiegało nasze doświadczenie, gdybyśmy nie utrudnili lince odwijania się ze stożka przez wbicie sztyftów (Rys. 1)?
Nie mam pojęcia, jak wyglądają poprawne odpowiedzi na te pytania. Ale może znajdzie się jakiś Przyrodnik, który wskaże, jaka jest relacja między tą scholastyczną matematyką a rzeczywistością. Taki werdykt niezbędny jest przy każdym powstającym matematycznym modelu zjawisk realnych, bo przecież takie modele, obecne dziś wszędzie, opisują niejednokrotnie zjawiska bardziej istotne niż zachowanie linki na stożku.