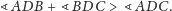Kącik przestrzenny
O pożytku ze sfery wpisanej
W tym kąciku chcielibyśmy powrócić do pewnych własności sfery wpisanej w czworościan, o których pisaliśmy w kąciku 2 o najmocniejszym twierdzeniu stereometrii (Delta 3/2010). Okazuje się, że można je wykorzystać do udowodnienia faktów pozornie niezwiązanych ze sferą wpisaną.
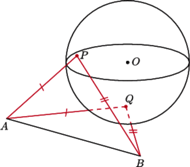
Rys. 1
Przypomnijmy więc główne twierdzenie:
Twierdzenie 1. Dana jest sfera
 i punkty
i punkty
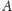 i
i
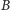 takie,
że prosta
takie,
że prosta
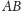 jest rozłączna ze sferą
jest rozłączna ze sferą
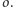 Prowadzimy dwie
płaszczyzny przechodzące przez punkty
Prowadzimy dwie
płaszczyzny przechodzące przez punkty
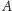 i
i
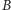 styczne do sfery
styczne do sfery
 w punktach
w punktach
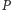 i
i
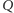 (Rys. 1). Wówczas trójkąty
(Rys. 1). Wówczas trójkąty
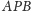 i
i
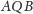 są przystające.
są przystające.
W kąciku 8 (Delta 6/2011) udowodniliśmy następujące twierdzenie:
Teraz zaprezentujemy inny dowód, wykorzystujący własności sfery wpisanej.
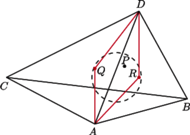
Rys. 2
Dowód. Niech
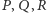 będą punktami
styczności sfery wpisanej w czworościan
będą punktami
styczności sfery wpisanej w czworościan
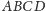 odpowiednio ze
ścianami
odpowiednio ze
ścianami
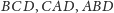 (Rys. 2).
Na mocy twierdzenia 1 trójkąty
(Rys. 2).
Na mocy twierdzenia 1 trójkąty
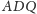 i
i
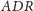 są przystające,
skąd
są przystające,
skąd
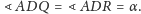 Analogicznie dostajemy
Analogicznie dostajemy

Wystarczy jeszcze zauważyć, że

Ta metoda nie wymaga rozważenia oddzielnie dwóch przypadków, jak dowód przeprowadzony w kąciku 8. Czytelnika Odważnego zaś zainteresuje fakt, że można w ten sposób udowodnić odpowiedniki twierdzenia 2 w wyższych wymiarach. Podobnie można uzasadnić inne ciekawe twierdzenie dotyczące czworościanu.
Twierdzenie 3. W dowolnym czworościanie pole każdej ściany jest mniejsze od sumy pól trzech pozostałych ścian.
Twierdzenie to jest odpowiednikiem nierówności trójkąta dla czworościanu. Zazwyczaj dowodzi się go poprzez zrzutowanie jednego z wierzchołków na płaszczyznę zawierającą przeciwległą ścianę i wykorzystanie faktu, że pole rzutu ściany nie przekracza pola ściany. Wykorzystanie najmocniejszego twierdzenia stereometrii pozwala przedstawić znacznie prostsze i zgrabniejsze uzasadnienie.
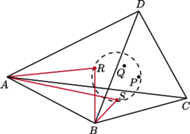
Rys. 3
Dowód. Należy wykazać, że w czworościanie
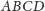 pole ściany
pole ściany
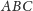 jest mniejsze od sumy pól trzech
pozostałych ścian. Oznaczmy przez
jest mniejsze od sumy pól trzech
pozostałych ścian. Oznaczmy przez
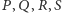 punkty styczności
sfery wpisanej w czworościan
punkty styczności
sfery wpisanej w czworościan
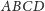 odpowiednio ze ścianami
odpowiednio ze ścianami
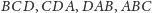 (Rys. 3). Z twierdzenia 1 wynika,
że trójkąty
(Rys. 3). Z twierdzenia 1 wynika,
że trójkąty
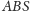 i
i
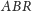 są przystające, a więc mają równe
pola. Podobnie dowodzimy równości pól
są przystające, a więc mają równe
pola. Podobnie dowodzimy równości pól

Ponieważ punkty
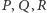 leżą wewnątrz ścian czworościanu, to
zachodzą nierówności
leżą wewnątrz ścian czworościanu, to
zachodzą nierówności

Zatem

Na koniec jedno zadanie dla Czytelników.