Deltoid
Łańcuch sfer
Tematem poprzedniego deltoidu była inwersja na płaszczyźnie. Analogicznie przekształcenie zdefiniować można w przestrzeni...
Definicja. Obrazem punktu
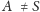 w inwersji względem
sfery o środku
w inwersji względem
sfery o środku
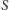 i promieniu
i promieniu
 jest taki punkt
jest taki punkt
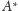 na
półprostej
na
półprostej
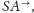 że
że
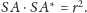
Oto niektóre własności inwersji w przestrzeni.
- obrazem punktu
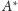 jest punkt
jest punkt
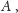
- obrazem sfery przechodzącej przez punkt
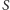 jest płaszczyzna
nieprzechodząca przez
jest płaszczyzna
nieprzechodząca przez
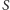 (i na odwrót),
(i na odwrót),
- obrazem sfery nieprzechodzącej przez
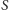 jest sfera
nieprzechodząca przez
jest sfera
nieprzechodząca przez
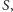
- obrazem okręgu nieprzechodzącego przez
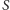 jest okrąg
nieprzechodzący przez
jest okrąg
nieprzechodzący przez
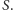
Punkt
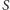 nazywa się środkiem inwersji. Nie definiujemy jego obrazu
nazywa się środkiem inwersji. Nie definiujemy jego obrazu
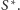
Wnioski
Po inwersji punkty styczności sfer
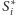 leżą na jednym okręgu. Nie
przechodzi on przez środek inwersji (bo środek ten jest wewnątrz sfery
leżą na jednym okręgu. Nie
przechodzi on przez środek inwersji (bo środek ten jest wewnątrz sfery
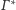 ), stąd także w wyjściowej sytuacji punkty styczności sfer
), stąd także w wyjściowej sytuacji punkty styczności sfer
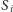 leżą na jednym okręgu.
leżą na jednym okręgu.
Dla każdej z płaszczyzn
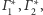 a także dla sfery
a także dla sfery
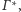 po inwersji
punkty styczności ze sferami
po inwersji
punkty styczności ze sferami
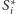 leżą na jednym okręgu. Stąd także
przed inwersją dla każdej ze sfer
leżą na jednym okręgu. Stąd także
przed inwersją dla każdej ze sfer
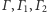 jej punkty styczności ze
sferami
jej punkty styczności ze
sferami
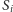 są na jednym okręgu.
są na jednym okręgu.
Po inwersji istnieją dwie sfery przechodzące przez środek inwersji oraz styczne
do wszystkich sfer
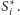 Można bowiem wyobrazić sobie, że sfera
Można bowiem wyobrazić sobie, że sfera
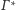 to balonik, który nadmuchujemy tak, by cały czas nadal był styczny do
wszystkich sfer
to balonik, który nadmuchujemy tak, by cały czas nadal był styczny do
wszystkich sfer
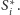 W miarę jak rośnie, „wypychamy” go do góry lub
do dołu. W każdym z tych dwóch wariantów istnieje dokładnie jedno
położenie, przy którym nasz balonik przechodzi przez środek inwersji.
Każda z takich dwóch sfer odpowiada wobec tego, w wyjściowej sytuacji,
płaszczyźnie i nadal jest styczna do wszystkich sfer
W miarę jak rośnie, „wypychamy” go do góry lub
do dołu. W każdym z tych dwóch wariantów istnieje dokładnie jedno
położenie, przy którym nasz balonik przechodzi przez środek inwersji.
Każda z takich dwóch sfer odpowiada wobec tego, w wyjściowej sytuacji,
płaszczyźnie i nadal jest styczna do wszystkich sfer
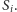 Istnieją zatem
takie dwie płaszczyzny styczne do wszystkich sfer
Istnieją zatem
takie dwie płaszczyzny styczne do wszystkich sfer
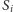 z góry i z dołu.
Ponadto, środki sfer
z góry i z dołu.
Ponadto, środki sfer
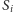 leżą wobec tego na jednej płaszczyźnie –
dwusiecznej kąta dwuściennego utworzonego przez te dwie płaszczyzny styczne
do sfer.
leżą wobec tego na jednej płaszczyźnie –
dwusiecznej kąta dwuściennego utworzonego przez te dwie płaszczyzny styczne
do sfer.