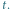Jak to działa?
Zegar słoneczny, równania różniczkowe i ładne obrazki
Nie od dziś wiadomo, jak zbudować najprostszy zegar słoneczny. Słońce, w swym pozornym ruchu po niebie, porusza się ze stałą prędkością kątową w płaszczyźnie prostopadłej do osi wskazującej północny biegun niebieski...

Rys. 1 Tarcza płaskiego zegara w Kętach
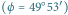 . Podziałka co godzinę.
. Podziałka co godzinę.

Rys. 2 Tarcza płaskiego zegara w Hyderabadzie
 .
.
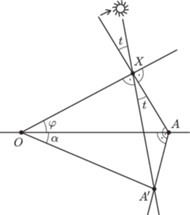
Rys. 3 Zmiana kąta w zegarze płaskim po obrocie Słońca o kąt
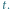
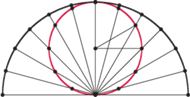
Rys. 4 Inna tarcza zegara na biegunie.
Aby zagwarantować niezależność odczytów od wysokości Słońca
nad horyzontem (czyli od pory roku), należy wycelować wskazówkę
zegara (gnomon) w Gwiazdę Polarną, czyli pod kątem odpowiadającym
lokalnej szerokości geograficznej
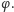 Jeżeli dodatkowo tarczę zegara
umieścimy prostopadle do wskazówki, to cień wskazówki będzie obracał się
jednostajnie i kolejne godziny możemy zaznaczać co
Jeżeli dodatkowo tarczę zegara
umieścimy prostopadle do wskazówki, to cień wskazówki będzie obracał się
jednostajnie i kolejne godziny możemy zaznaczać co
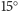 (oczywiście,
mówimy tu o pomiarze lokalnego czasu słonecznego). Więcej w Delcie
8/2010.
(oczywiście,
mówimy tu o pomiarze lokalnego czasu słonecznego). Więcej w Delcie
8/2010.
Jeżeli chcemy, aby cień rzucany był po prostu na powierzchnię Ziemi
(zegar horyzontalny), to równomierna podziałka działa tylko na biegunie.
O ile w naszych szerokościach geograficznych, dajmy na to w Kętach
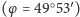 , tarcza zegara płaskiego nie wygląda źle (Rys. 1), o tyle
w Hyderabadzie
, tarcza zegara płaskiego nie wygląda źle (Rys. 1), o tyle
w Hyderabadzie
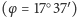 zagęszczenie wokół południa jest już
spore (Rys. 2). Pogarsza to czytelność zegara w tych godzinach i może
prowadzić do nadmiernego rozwleczenia pory lunchu, ze szkodą dla
gospodarki.
zagęszczenie wokół południa jest już
spore (Rys. 2). Pogarsza to czytelność zegara w tych godzinach i może
prowadzić do nadmiernego rozwleczenia pory lunchu, ze szkodą dla
gospodarki.
Łatwo sprawdzić, dlaczego tak jest. Ustalmy dla uproszczenia rachunków,
że lokalne południe wypada w chwili
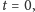 a lokalna godzina
18:00 w chwili
a lokalna godzina
18:00 w chwili
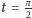 (to znaczy mierzymy czas prędkością kątową
Słońca). Z rysunku 3 widzimy, że przesunięciu Słońca po niebie o kąt
(to znaczy mierzymy czas prędkością kątową
Słońca). Z rysunku 3 widzimy, że przesunięciu Słońca po niebie o kąt
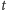 odpowiada obrót cienia o kąt
odpowiada obrót cienia o kąt
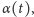 przy czym
przy czym
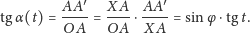 | (1) |
Jeśli więc
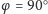 (biegun północny), to
(biegun północny), to
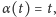 czyli cień
obraca się jednostajnie i w zegarze poziomym można użyć równomiernej
podziałki. Gdy kąt
czyli cień
obraca się jednostajnie i w zegarze poziomym można użyć równomiernej
podziałki. Gdy kąt
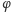 maleje, spada także
maleje, spada także
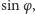 a przez to kąt
a przez to kąt
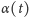 zmienia się niejednostajnie wraz z
zmienia się niejednostajnie wraz z
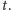

Rys. 5 Kolejna tarcza na biegunie...

Rys. 6 ...i jej poprawiona wersja.
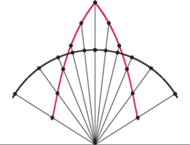
Rys. 7 Utrzymując stałą prędkość, nie uda się „dociągnąć” do godziny szóstej.
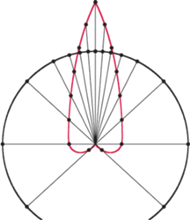
Rys. 8 Przykład zegara w Hyderabadzie...

Rys. 9 ...w Luksorze...

Rys. 10 …i w Kętach.
Ten efekt (lub defekt) można rekompensować, manipulując kształtem tarczy.
Umówmy się, że godzinę odczytujemy na przecięciu cienia z krzywą
wyznaczającą brzeg zegara. Najbardziej wymagający esteta (na przykład jeden
z autorów tego tekstu) mógłby chcieć, aby pomiędzy każdymi dwiema
chwilami
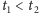 kraniec cienia pokonywał fragment tej krzywej
o długości proporcjonalnej do
kraniec cienia pokonywał fragment tej krzywej
o długości proporcjonalnej do
 Powinno to pomóc rozładować
lokalne „zagęszczenia”. Skoro pokonywana droga ma być proporcjonalna do
czasu, to punkt odczytu musi przemieszczać się ze stałą prędkością.
Wkraczamy tu w obszar geometrii różniczkowej krzywych. Jeżeli punkt
przemieszcza się po płaszczyźnie tak, że w chwili
Powinno to pomóc rozładować
lokalne „zagęszczenia”. Skoro pokonywana droga ma być proporcjonalna do
czasu, to punkt odczytu musi przemieszczać się ze stałą prędkością.
Wkraczamy tu w obszar geometrii różniczkowej krzywych. Jeżeli punkt
przemieszcza się po płaszczyźnie tak, że w chwili
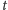 znajduje się
w punkcie
znajduje się
w punkcie
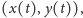 to jego prędkość w chwili
to jego prędkość w chwili
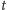 ma
wartość
ma
wartość

co wynika z twierdzenia Pitagorasa zastosowanego do prędkości w kierunkach
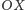 (u nas zachód-wschód) i
(u nas zachód-wschód) i
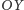 (południe-północ). Wiemy
już, że w chwili
(południe-północ). Wiemy
już, że w chwili
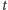 obwiednia każdego zegara musi przechodzić przez
punkt odchylony od osi
obwiednia każdego zegara musi przechodzić przez
punkt odchylony od osi
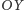 o kąt
o kąt
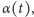 w takim razie jest opisana
parametryzacją
w takim razie jest opisana
parametryzacją

Warunek stałej prędkości przyjmuje postać

Zakładając, bez straty ogólności, że
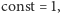 dochodzimy do
równania
dochodzimy do
równania

Czytelnicy zaznajomieni z zasadami różniczkowania funkcji trygonometrycznych
mogą wyprowadzić z równania (1) wzór na
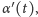 za pomocą
którego dostaniemy ostatecznie równanie różniczkowe na promień
za pomocą
którego dostaniemy ostatecznie równanie różniczkowe na promień
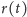 :
:
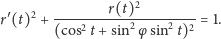 | (2) |
Zanim wrócimy do Kęt i Hyderabadu, zatrzymajmy się nad tym równaniem
na biegunie. Wtedy
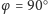 i szukamy funkcji
i szukamy funkcji
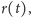 dla
której
dla
której

Taką własność ma niewątpliwie funkcja stała
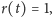 co daje omawiany
już zegar biegunowy o tarczy w kształcie okręgu. Nie jest to jednak jedyna
możliwość! Możemy, na przykład, wziąć
co daje omawiany
już zegar biegunowy o tarczy w kształcie okręgu. Nie jest to jednak jedyna
możliwość! Możemy, na przykład, wziąć
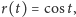 otrzymując
krzywą
otrzymując
krzywą
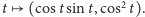 Jest ona przedstawiona na rysunku 4 wraz
z punktami, w których wypadał będzie cień w kolejnych pełnych godzinach.
Jest to w istocie okrąg o środku
Jest ona przedstawiona na rysunku 4 wraz
z punktami, w których wypadał będzie cień w kolejnych pełnych godzinach.
Jest to w istocie okrąg o środku
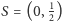 (proszę sprawdzić!). Co
więcej, mogliśmy dokonać tego odkrycia, używając elementarnej geometrii
(choć jeden z autorów tego tekstu nigdy by się o to nie podejrzewał).
Wyjaśnienie znajduje się także na rysunku 4: skoro kąt wpisany zmienia się ze
stałą prędkością, to także kąt środkowy zmienia się ze stałą, dwa razy większą
prędkością, a więc punkt odczytu czasu obiega
(proszę sprawdzić!). Co
więcej, mogliśmy dokonać tego odkrycia, używając elementarnej geometrii
(choć jeden z autorów tego tekstu nigdy by się o to nie podejrzewał).
Wyjaśnienie znajduje się także na rysunku 4: skoro kąt wpisany zmienia się ze
stałą prędkością, to także kąt środkowy zmienia się ze stałą, dwa razy większą
prędkością, a więc punkt odczytu czasu obiega
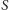 jednostajnie. Możemy
też wziąć dowolną kombinację
jednostajnie. Możemy
też wziąć dowolną kombinację
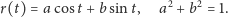 | (3) |
Krzywe opisane tego typu promieniem to okręgi przechodzące przez punkt
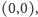 jak na rysunku 5. Praktyczna przydatność takiego zegara stoi
pod znakiem zapytania, bo niektóre godziny wskazuje nie sam cień, a raczej
jego niewidoczne przedłużenie w przeciwną stronę od początku układu.
Można temu zaradzić, biorąc symetryczne odbicie odpowiedniego
fragmentu, co daje krzywą o stałej prędkości, ale nie wszędzie gładką
(Rys. 6). Może jednak na biegun lepiej zabrać bardziej nowoczesny
czasomierz.
jak na rysunku 5. Praktyczna przydatność takiego zegara stoi
pod znakiem zapytania, bo niektóre godziny wskazuje nie sam cień, a raczej
jego niewidoczne przedłużenie w przeciwną stronę od początku układu.
Można temu zaradzić, biorąc symetryczne odbicie odpowiedniego
fragmentu, co daje krzywą o stałej prędkości, ale nie wszędzie gładką
(Rys. 6). Może jednak na biegun lepiej zabrać bardziej nowoczesny
czasomierz.
To już wszystkie rozwiązania równania (2). Niekompletny szkic dowodu,
którego szczegóły zainteresowany Czytelnik może uzupełnić we
własnym zakresie, jest następujący: skoro
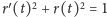 to,
różniczkując, dostajemy
to,
różniczkując, dostajemy
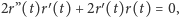 a więc
a więc
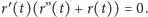 W takim razie albo
W takim razie albo
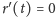 i
i
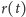 jest
stałą, albo
jest
stałą, albo
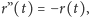 a wtedy
a wtedy
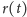 musi być postaci
(3).
musi być postaci
(3).
Wróćmy do szerokości geograficznych o nieco cieplejszym klimacie. Dla
dowolnego
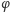 równanie (2) jest bardziej skomplikowane i autorzy nie
znają żadnego jawnego wzoru na jego rozwiązanie
równanie (2) jest bardziej skomplikowane i autorzy nie
znają żadnego jawnego wzoru na jego rozwiązanie
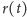 (może ktoś
z Czytelników?). Nic nie stoi jednak na przeszkodzie, aby znaleźć rozwiązanie
numerycznie lub przybliżyć je eksperymentalnie, na przykład łamaną o stałej
odległości między każdymi dwiema pełnymi godzinami. Możemy
manipulować początkową wartością promienia
(może ktoś
z Czytelników?). Nic nie stoi jednak na przeszkodzie, aby znaleźć rozwiązanie
numerycznie lub przybliżyć je eksperymentalnie, na przykład łamaną o stałej
odległości między każdymi dwiema pełnymi godzinami. Możemy
manipulować początkową wartością promienia
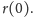 Gdy zaczniemy
zbyt daleko od początku układu, rozwiązanie może istnieć tylko przez pewien
czas, a potem krzywa nie będzie miała wystarczającego zapasu prędkości, aby
nadążyć za coraz szybciej uciekającym cieniem (Rys. 7). Poniżej pewnej
krytycznej wartości rozwiązanie równania istnieje bardzo długo, aż do godzin
nocnych, gdy Słońca już dawno nie widać. Mamy też swobodę w łączeniu
kilku gładkich fragmentów, jak w przykładzie na biegunie. Kilka ładnych
zegarów o stałej prędkości cienia po brzegu tarczy przedstawionych jest na
rysunkach 8-10.
Gdy zaczniemy
zbyt daleko od początku układu, rozwiązanie może istnieć tylko przez pewien
czas, a potem krzywa nie będzie miała wystarczającego zapasu prędkości, aby
nadążyć za coraz szybciej uciekającym cieniem (Rys. 7). Poniżej pewnej
krytycznej wartości rozwiązanie równania istnieje bardzo długo, aż do godzin
nocnych, gdy Słońca już dawno nie widać. Mamy też swobodę w łączeniu
kilku gładkich fragmentów, jak w przykładzie na biegunie. Kilka ładnych
zegarów o stałej prędkości cienia po brzegu tarczy przedstawionych jest na
rysunkach 8-10.
Jedne z bardziej efektownych zegarów słonecznych znajdują się na budynkach, a więc na pionowych ścianach, i to niekoniecznie zwróconych na południe. Zainteresowanym Czytelnikom polecamy przeniesienie naszej konstrukcji np. na ścianę swojego domu.
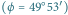 . Podziałka co godzinę.
. Podziałka co godzinę.
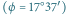 .
.