Kącik przestrzenny
O sumie długości krawędzi czworościanu
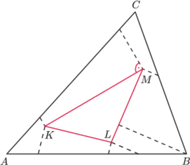
Rys. 1
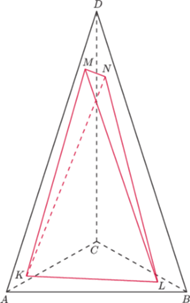
Rys. 2
Fakt. Jeśli na płaszczyźnie wewnątrz trójkąta
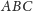 znajduje się
trójkąt
znajduje się
trójkąt
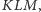 to obwód trójkąta
to obwód trójkąta
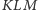 jest nie większy od
obwodu trójkąta
jest nie większy od
obwodu trójkąta
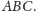
Pomysł, na którym opiera się dowód tego faktu, został przedstawiony na
rysunku 1. W podobny sposób można udowodnić, że jeśli czworościan
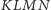 znajduje się wewnątrz czworościanu
znajduje się wewnątrz czworościanu
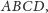 to jego pole
powierzchni jest mniejsze od pola powierzchni
to jego pole
powierzchni jest mniejsze od pola powierzchni
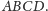 A co umiemy
powiedzieć o sumie długości krawędzi?
A co umiemy
powiedzieć o sumie długości krawędzi?
Jeśli czworościan
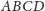 jest foremny, to jego krawędzie mają długości
nie mniejsze od długości krawędzi czworościanu
jest foremny, to jego krawędzie mają długości
nie mniejsze od długości krawędzi czworościanu
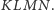 W takim
razie suma długości krawędzi czworościanu
W takim
razie suma długości krawędzi czworościanu
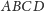 jest nie mniejsza od
sumy długości krawędzi czworościanu
jest nie mniejsza od
sumy długości krawędzi czworościanu
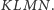 Jednak w ogólności
nie musi tak być.
Jednak w ogólności
nie musi tak być.
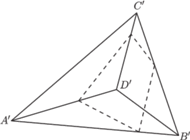
Rozważmy mianowicie ostrosłup prawidłowy
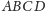 o podstawie
o podstawie
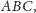 która ma boki długości
która ma boki długości
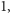 i ramionach długości
i ramionach długości
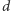 (Rys. 2). Umieśćmy wewnątrz niego czworościan
(Rys. 2). Umieśćmy wewnątrz niego czworościan
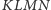 w taki
sposób, że wierzchołek
w taki
sposób, że wierzchołek
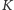 jest blisko
jest blisko
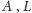 – blisko
– blisko
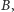 zaś
zaś
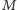 i
i
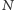 blisko wierzchołka
blisko wierzchołka
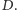 Wtedy
suma krawędzi ostrosłupa
Wtedy
suma krawędzi ostrosłupa
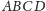 jest równa
jest równa
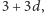 zaś
suma krawędzi czworościanu
zaś
suma krawędzi czworościanu
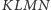 jest większa od sumy
jest większa od sumy
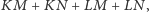 która może być dowolnie bliska
która może być dowolnie bliska
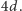 Jeśli
więc weźmiemy
Jeśli
więc weźmiemy
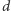 znacznie większe niż
znacznie większe niż
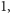 to suma długości
krawędzi czworościanu
to suma długości
krawędzi czworościanu
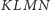 będzie większa od sumy długości
krawędzi czworościanu
będzie większa od sumy długości
krawędzi czworościanu
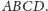
Widzimy zatem, że podany na początku fakt nie przenosi się z płaszczyzny na
przestrzeń. Jednak w obu powyższych przykładach suma długości krawędzi
czworościanu
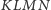 nie przekracza
nie przekracza
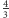 sumy długości
krawędzi czworościanu
sumy długości
krawędzi czworościanu
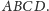 I właśnie to spostrzeżenie
udowodnimy:
I właśnie to spostrzeżenie
udowodnimy:
Twierdzenie. Jeśli czworościan
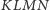 jest zawarty wewnątrz
czworościanu
jest zawarty wewnątrz
czworościanu
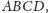 to suma długości jego krawędzi jest nie
większa od
to suma długości jego krawędzi jest nie
większa od
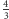 sumy długości krawędzi czworościanu
sumy długości krawędzi czworościanu
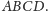
Powyższy problem był jednym z zadań na finale olimpiady w ZSRR w 1982 roku. Dowód podzielimy na kilka podproblemów. Dalej podajemy rozwiązania, ale zachęcamy do samodzielnej pracy.
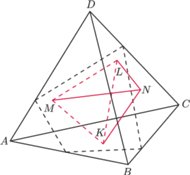
Rys. 3
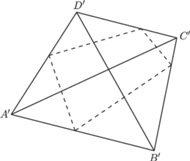
Rys. 4
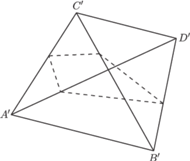
Rys. 5
Krok 1. Załóżmy bez straty dla ogólności, że
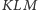 jest ścianą
o największym obwodzie. Wtedy suma długości krawędzi czworościanu
jest ścianą
o największym obwodzie. Wtedy suma długości krawędzi czworościanu
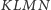 nie przekracza dwukrotności obwodu trójkąta
nie przekracza dwukrotności obwodu trójkąta
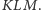
Krok 2. Załóżmy, że
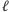 jest obwodem wielokąta będącego przekrojem
czworościanu
jest obwodem wielokąta będącego przekrojem
czworościanu
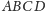 płaszczyzną
płaszczyzną
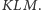 Wtedy obwód trójkąta
Wtedy obwód trójkąta
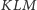 nie przekracza
nie przekracza
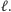
Krok 3. Niech
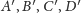 będą odpowiednio rzutami prostokątnymi
punktów
będą odpowiednio rzutami prostokątnymi
punktów
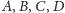 na płaszczyznę
na płaszczyznę
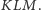 Wtedy suma długości
wszystkich odcinków łączących punkty
Wtedy suma długości
wszystkich odcinków łączących punkty
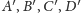 jest nie mniejsza
niż
jest nie mniejsza
niż
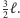 (Ten fragment dowodu jest najtrudniejszy.)
(Ten fragment dowodu jest najtrudniejszy.)
Krok 4. Suma długości odcinków łączących punkty
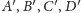 jest nie
większa niż suma długości krawędzi czworościanu
jest nie
większa niż suma długości krawędzi czworościanu
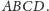
Rozwiązania
Krok 1. Suma długości krawędzi czworościanu
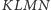 jest równa
połowie sumy obwodów wszystkich czterech jego ścian. Ta ostatnia zaś nie
może przekraczać dwukrotności obwodu ściany o największym
obwodzie.
jest równa
połowie sumy obwodów wszystkich czterech jego ścian. Ta ostatnia zaś nie
może przekraczać dwukrotności obwodu ściany o największym
obwodzie.
Krok 2. Pomysł przedstawiony na rysunku 1 działa i w tej sytuacji.
Rys. 6
Krok 3. Załóżmy najpierw, że punkty
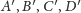 są wierzchołkami
czworokąta wypukłego. (Oczywiście punkty te mogą leżeć na obwodzie
czworokąta w różnej kolejności!) Rozważany przekrój czworościanu jest
wypukły i leży wewnątrz tego czworokąta (Rys. 4 i 5). Zatem
są wierzchołkami
czworokąta wypukłego. (Oczywiście punkty te mogą leżeć na obwodzie
czworokąta w różnej kolejności!) Rozważany przekrój czworościanu jest
wypukły i leży wewnątrz tego czworokąta (Rys. 4 i 5). Zatem
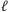 nie
może przekraczać obwodu czworokąta o wierzchołkach
nie
może przekraczać obwodu czworokąta o wierzchołkach
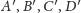 (dowód jak na rysunku 1). Ponadto z nierówności trójkąta wiemy, że suma
długości przekątnych czworokąta wypukłego jest większa od połowy jego
obwodu. Łącząc te dwie nierówności, dostajemy
(dowód jak na rysunku 1). Ponadto z nierówności trójkąta wiemy, że suma
długości przekątnych czworokąta wypukłego jest większa od połowy jego
obwodu. Łącząc te dwie nierówności, dostajemy

Przyjmijmy teraz, że jeden z tych punktów (np.
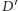 ) leży wewnątrz lub
na brzegu trójkąta wyznaczonego przez pozostałe punkty. Podobnie
stwierdzamy, że rozważany przekrój jest wypukły i leży wewnątrz tego
trójkąta (Rys. 6). Zatem
) leży wewnątrz lub
na brzegu trójkąta wyznaczonego przez pozostałe punkty. Podobnie
stwierdzamy, że rozważany przekrój jest wypukły i leży wewnątrz tego
trójkąta (Rys. 6). Zatem

Z nierówności trójkąta otrzymujemy

I tym razem te dwie nierówności dają żądane oszacowanie.
Krok 4. Wynika to natychmiast z faktu, że długość odcinka nie może być mniejsza niż długość jego rzutu prostokątnego na dowolną płaszczyznę.