Stowarzyszenie na rzecz Edukacji Matematycznej
Wszystko może się przydać
Panuje przekonanie, że w nauczaniu matematyki powinno się eksponować fakt, że ma ona zastosowania. Gdy przyjrzeć się podręcznikom, a zwłaszcza testom kwalifikacyjnym, trudno oprzeć się wrażeniu, że są to rzeczy w stylu mierzenia wysokości piramidy za pomocą długości jej cienia i twierdzenia Talesa, lub też zadań w stylu: jeśli dwóch robotników kopie rów w ciągu 2 godzin, to ilu ich potrzeba, aby ten rów wykopać w 15 sekund? (odpowiedź: 1440).
Aby pomóc w przełamaniu tej wstydliwej sytuacji, chcę podać przykład konkretnego, przemysłowego wykorzystania prostego faktu stereometrycznego.
Każdy wie, że płytki odblaskowe naszywane na ubrania czy przyczepiane do rowerów zbudowane są z wielu malutkich naroży złożonych z trzech lusterek, z których każde jest prostopadłe do pozostałych. Bierze się to z faktu, iż
Fakt. Złożenie trzech symetrii względem płaszczyzn parami prostopadłych to symetria względem punktu ich przecięcia, a wobec tego każdy promień jest odbijany jako równoległy do padającego, czyli wraca w kierunku źródła padającego światła.
Prosty dowód jest taki:
Dowód. Potraktujmy krawędzie przecięcia płaszczyzn jak osie układu
współrzędnych – wtedy symetrie względem płaszczyzn będą odpowiadały
zmianie znaku jednej ze współrzędnych. Wobec tego z punktu
o współrzędnych
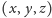 otrzymamy punkt
otrzymamy punkt
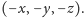
I jeszcze wniosek:
Wniosek. Aby otrzymać symetrię względem danego punktu, można dowolnie obrać przechodzące przez niego płaszczyzny, byle były wzajemnie prostopadłe.
Ale nie o to zastosowanie mi tu chodzi. W wielu celownikach optycznych (tak, chodzi o uzbrojenie!) potrzebne jest ustawienie dwóch lusterek dokładnie pod kątem prostym. Jak łatwo zgadnąć, uzyskanie tego przez korygowanie ustawienia, aż będzie dostatecznie dokładne, jest i pracochłonne, i nie do końca precyzyjne.
Ale można tu wykorzystać wzmocnienie powyżej wyróżnionego twierdzenia:
Twierdzenie. Złożenie trzech symetrii względem płaszczyzn jest symetrią względem punktu ich przecięcia wtedy i tylko wtedy, gdy płaszczyzny te są parami prostopadłe.
Dowód. Przypuśćmy,
że symetrię względem punktu
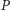 można otrzymać ze złożenia
symetrii względem płaszczyzn
można otrzymać ze złożenia
symetrii względem płaszczyzn
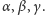 Weźmy teraz przechodzące
przez
Weźmy teraz przechodzące
przez
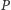 prostopadłe płaszczyzny
prostopadłe płaszczyzny
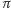 i
i
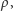 które są
prostopadłe również do
które są
prostopadłe również do
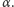 Mamy więc
Mamy więc

W ostatniej równości mamy do czynienia z dwoma obrotami, a zatem
kąt między wyznaczającymi je płaszczyznami musi być taki sam.
Stąd
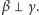 Podobnie wykazujemy prostopadłość
Podobnie wykazujemy prostopadłość
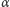 do
do
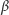 i
i
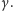
Skoro tak, to można prostopadłość dwóch luster sprawdzać, patrząc, czy da się do nich dostawić trzecie tak, aby odbijały każdy promień jako równoległy.
Każdy to brzmi strasznie. Ale zastanówmy się, czy nie wystarczy sprawdzić odbicia tylko np. dla trzech różnych kierunków. Czytelnik Zmyślny od razu będzie wiedział, że nie. Ale może wystarczy dla czterech?
Kolejny problem to (gdy już ustalimy skończoną listę kierunków do sprawdzenia), jak sprawdzić, czy odbity promień jest równoległy do padającego?
Przytoczony przykład jest autentyczny. Przypomniał mi się, bo 5 lipca zmarł mój kolega, Ludomir Włodarski (napisaliśmy nawet wspólnie książkę O geometrii dla postronnych; dla Delty napisał wspólnie z Maciejem Bryńskim pierwszy tomik Biblioteczki Delty o konstrukcjach geometrycznych). Był bardzo uzdolnionym geometrą, ale prawdziwą sensacją był (wówczas – połowa lat siedemdziesiątych – praktycznie niespotykany) fakt, że bezpośrednio po doktoracie poszedł pracować do przemysłu, do Polskich Zakładów Optycznych. Usprawnienie kontroli prostopadłości luster, oparte na opisanym tu pomyśle, było jego pierwszym dokonaniem w nowym miejscu pracy. Potem, rzecz jasna, doprowadził do wykorzystania wielu poważniejszych twierdzeń geometrii (zwłaszcza rzutowej) w praktyce przemysłowej.