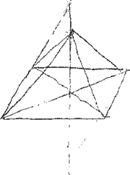
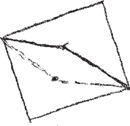
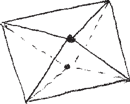
Zazwyczaj rysujemy go, startując od piramidy o podstawie kwadratowej. Rysujemy więc równoległobok (Rys. 1). Pomocniczo zaznaczamy przekątne (Rys. 2).

Rys. 1

Rys. 2

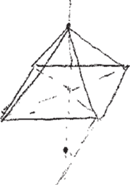
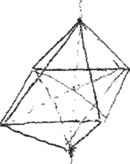
Z punktu ich przecięcia prowadzimy wysokość; musi być ona nieco krótsza od krawędzi. Wierzchołek wybieramy tak, by nie leżał na przedłużeniu krawędzi podstawy (Rys. 3). Ośmiościan to sklejone podstawami dwie piramidy, więc tę wysokość przedłużamy w drugą stronę – długość powinna być mniej więcej taka sama (Rys. 4). Wreszcie łączymy końce wysokości z wierzchołkami podstawy i dostajemy klasyczny ośmiościan (Rys. 5).

Rys. 3

Rys. 4

Rys. 5

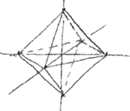
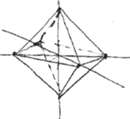
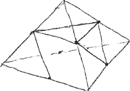
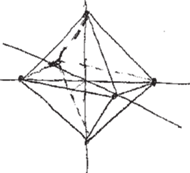
Można jednak postąpić inaczej. Rysujemy pomocniczo dwie proste prostopadłe (Rys. 6). Potem jeszcze trzecią przechodzącą przez ich punkt przecięcia, jak w przestrzennym układzie współrzędnych (Rys. 7). Teraz na prostych prostopadłych od tegoż punktu przecięcia odkładamy w jednakowych odległościach punkty. Na prostej pochyłej te odległości powinny być nieco mniejsze (wiadomo, chodzi o skrócenie, Rys. 8).

Rys. 6

Rys. 7

Rys. 8

Łączymy każdy z zaznaczonych punktów z pozostałymi z wyjątkiem tego przeciwległego (Rys. 9). Wybrane odcinki, te niewidoczne, rysujemy np. linią przerywaną (Rys. 10). Dostajemy ośmiościan lekko obrócony wokół pionowej osi. „Stopień” obrócenia możemy kontrolować poprzez odpowiedni dobór trzeciej prostej (Rys. 11).

Rys. 9

Rys. 10

Rys. 11

Otrzymany ośmiościan niejako stoi na wierzchołku. A gdyby tak spróbować narysować leżący ośmiościan?

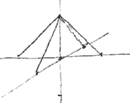
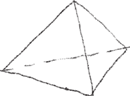
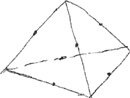
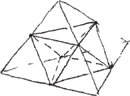
To wcale nie jest trudne. Zaczynamy od narysowania w pozycji standardowej czworościanu pełniącego rolę pomocniczą (Rys. 12). Teoria głosi, że środki krawędzi czworościanu są właśnie wierzchołkami ośmiościanu. Wykorzystajmy więc to i w narysowanym czworościanie zaznaczmy środki krawędzi (Rys. 13).

Następnie w każdym z trójkątów trzeba połączyć pary punktów (Rys. 14), pamiętając, że rysowane odcinki powinny być równoległe do odpowiednich odcinków (dlaczego?). Otrzymamy ośmiościan leżący na jednej ze ścian (Rys. 15).

Rys. 12

Rys. 13

Rys. 14

Rys. 15

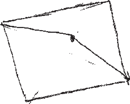
Jeśli przyjrzymy się bliżej tak powstałemu ośmiościanowi, zauważymy, że można go narysować jeszcze inaczej, bez pomocniczego czworościanu. Rysujemy równoległobok (taki bliższy rombowi), wewnątrz wybieramy punkt nieleżący na żadnej przekątnej (Rys. 16) i łączymy go z dwoma przeciwległymi wierzchołkami (Rys. 17). Z wierzchołków tych wyprowadzamy po jeszcze jednym odcinku równoległym do odcinka wychodzącego z punktu przeciwległego (Rys. 18). Teraz wystarczy odpowiednio dopełnić rysunek czterema odcinkami wychodzącymi z pozostałych wierzchołków (Rys. 19).

Rys. 16

Rys. 17

Rys. 18

Rys. 19

Prawda, że nie jest to takie trudne?

Pisał i rysował Zdzisław POGODA