Wszystkie zadania z odbytych już etapów obecnej Olimpiady (także z wielu poprzednich) i ich rozwiązania można znaleźć na stronie internetowej Olimpiady.

Najtrudniejszym zadaniem w pierwszym stopniu okazało się przedostatnie zadanie (stereometria), które w całym kraju rozwiązało jedynie 29 osób. Trudne też było dwunaste zadanie, ale z nim dały sobie radę 222 osoby. Najłatwiejsze w pierwszym stopniu było zadanie trzecie (geometria płaska), z którym poradziło sobie 1076 Osób.

W zawodach drugiego stopnia najtrudniejsza okazała się geometria przestrzenna ku zaskoczeniu części członków komisji przygotowującej zadania na zawody. Rozwiązało je poprawnie około 80 osób, drugie w kolejności było zadanie piąte (geometria płaska), które rozwiązało nieco ponad 90 osób – dokładne liczby w czasie pisania tekstu jeszcze nie są znane. Najłatwiejszym zadaniem tego etapu było zadanie pierwsze (układ równań), które rozwiązało 216 osób, czyli około 36% uczestników II stopnia OM. Chce się powiedzieć tylko 216 osób, bo układ równań nie był standardowy z punktu widzenia tego, co pojawia się w liceach, ale też nie był trudny.

Autora tego tekstu zaskoczyła trudność zadania z geometrii przestrzennej:

Rzecz w tym, że zadanie można rozwiązać momentalnie, i to w pamięci, posługując się tzw. współrzędnymi barycentrycznymi, o których można coś przeczytać w artykule Marka Kordosa ]Co nam mogą dać ciężary i wypory? opublikowanym w Delcie 3/2012. Każdy punkt czworościanu traktujemy jako środek masy układu złożonego z czterech jego wierzchołków, w których umieszczono odpowiednie masy. 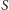Wybór tych mas jest jednoznaczny, jeśli ich sumą jest  Środek ciężkości  czworościanu 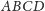 otrzymujemy, umieszczając w wierzchołkach równe masy: 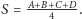 We wspomnianym artykule M.K. wyjaśnił, że chcąc potraktować punkt 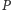 trójkąta 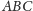 jako środek masy układu trzech punktów materialnych, należy w wierzchołkach 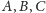 umieścić masy równe polom trójkątów 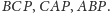 W przypadku punktu 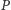 czworościanu 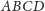 zastępujemy pola trójkątów leżących naprzeciw wierzchołków objętościami przeciwległych czworościanów, np. w punkcie 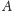 umieszczamy masę równą objętości czworościanu 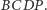 Środek 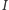 sfery wpisanej w czworościan otrzymujemy, umieszczając w wierzchołkach masy równe polom przeciwległych ścian, bo w tym przypadku wysokości czterech ostrosłupów są równe jako promienie sfery wpisanej. Przy okazji: środek okręgu wpisanego w trójkąt otrzymujemy, gdy masy są równe długościom przeciwległych boków – Czytelniku, przypomnij sobie twierdzenie o dwusiecznej! Wobec tego

gdzie 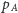 to pole trójkąta 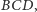 analogicznie definiujemy 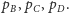 Wektory

są równoległe wtedy i tylko wtedy, gdy trójki współczynników

są proporcjonalne, a więc gdy

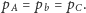
Na marginesie ostatniego zadania drugiego stopnia OM:

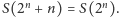chciałbym zapytać Czytelników Delty o prawdziwość stwierdzenia: dla nieskończenie wielu  zachodzi równość  Jeśli tak, to czy ta równość zachodzi dla nieskończenie wielu 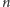 postaci  ?
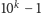