Mała Delta
Odkryj twierdzenie sam
Czasem przydaje się do czegoś twierdzenie o dwusiecznej...
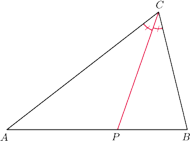
Rys. 1
Twierdzenie (o dwusiecznej). Jeśli w trójkącie
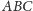 poprowadzimy dwusieczną kąta
poprowadzimy dwusieczną kąta
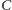 przecinającą odcinek
przecinającą odcinek
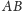 w punkcie
w punkcie
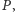 to stosunek długości odcinków
to stosunek długości odcinków
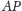 i
i
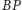 będzie
równy stosunkowi długości boków
będzie
równy stosunkowi długości boków
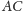 i
i
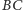 (Rys. 1).
(Rys. 1).
O trudnych zadaniach i efektownych rozwiązaniach, w których ma ono swój udział, można by długo pisać, ale tym razem spojrzymy na nie od innej strony: ciekawe, czy istnieje jego odpowiednik w geometrii przestrzennej?
Żeby otrzymać podobną zależność dla czworościanu, należałoby pewnie wziąć płaszczyznę dwusieczną kąta dwuściennego i jej punkt przecięcia z przeciwległą krawędzią. Stosunek długości odcinków, na które dzieli ją ta płaszczyzna, powinien być równy... no właśnie, czemu?
Weźmy jakiś szczególny czworościan i sprawdźmy, co dla niego wychodzi. Na przykład, co się dzieje dla czworościanu foremnego?
W tym przypadku dwusieczna kąta dwuściennego dzieli czworościan na
symetryczne części i ten stosunek jest równy
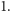 Wydaje się, że
podobnie jak dla trójkąta, powinniśmy umieć zapisać ten stosunek jako
iloraz dwóch wielkości zależnych od ścian wybranego kąta dwuściennego.
Niestety, pierwszy przykład wygląda na zbyt szczególny, ponieważ każdy ze
stosunków: pól, obwodów, wysokości, krawędzi wychodzących z tego
samego wierzchołka jest także równy
Wydaje się, że
podobnie jak dla trójkąta, powinniśmy umieć zapisać ten stosunek jako
iloraz dwóch wielkości zależnych od ścian wybranego kąta dwuściennego.
Niestety, pierwszy przykład wygląda na zbyt szczególny, ponieważ każdy ze
stosunków: pól, obwodów, wysokości, krawędzi wychodzących z tego
samego wierzchołka jest także równy
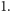 Trzeba pomyśleć nad
lepszym przykładem do testowania.
Trzeba pomyśleć nad
lepszym przykładem do testowania.
Rys. 2a
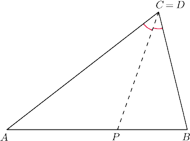
Rys. 2b
Spróbujmy może wziąć taki czworościan
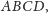 aby spodek
wysokości poprowadzonej z wierzchołka
aby spodek
wysokości poprowadzonej z wierzchołka
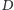 na podstawę
na podstawę
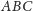 pokrywał się z punktem
pokrywał się z punktem
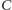 (inaczej mówiąc, krawędź
(inaczej mówiąc, krawędź
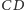 ma być prostopadła do ściany
ma być prostopadła do ściany
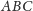 ), i popatrzeć na
płaszczyznę dwusieczną kąta dwuściennego przy krawędzi
), i popatrzeć na
płaszczyznę dwusieczną kąta dwuściennego przy krawędzi
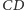 (Rys. 2a).
(Rys. 2a).
Dlaczego to dobry przykład? Widzimy, że część wspólna płaszczyzny
dwusiecznej kąta dwuściennego przy krawędzi
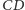 z płaszczyzną
z płaszczyzną
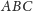 jest dwusieczną kąta
jest dwusieczną kąta
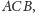 czyli na podstawie
czyli na podstawie
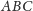 mamy narysowaną sytuację z płaskiej wersji twierdzenia
o dwusiecznej (Rys. 2b).
mamy narysowaną sytuację z płaskiej wersji twierdzenia
o dwusiecznej (Rys. 2b).
A dlaczego tak jest? Zauważmy, że płaszczyzna dwusieczna dzieli kąt
dwuścienny na połowy. Kąt dwuścienny zaś jest równy kątowi płaskiemu
utworzonemu przez dwie proste leżące w półpłaszczyznach go ograniczających
i prostopadłe do wspólnej krawędzi. Wybraliśmy czworościan tak, żeby
prosta
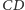 była prostopadła do płaszczyzny
była prostopadła do płaszczyzny
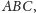 a więc
w szczególności do prostych
a więc
w szczególności do prostych
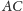 i
i
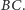 To oznacza, że proste
To oznacza, że proste
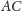 i
i
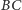 tworzą kąt płaski równy kątowi dwuściennemu między
wybranymi ścianami.
tworzą kąt płaski równy kątowi dwuściennemu między
wybranymi ścianami.
Teraz, jeśli przez
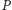 oznaczymy punkt przecięcia płaszczyzny dwusiecznej
kąta dwuściennego przy krawędzi
oznaczymy punkt przecięcia płaszczyzny dwusiecznej
kąta dwuściennego przy krawędzi
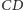 z krawędzią
z krawędzią
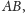 to
na mocy twierdzenia o dwusiecznej mamy
to
na mocy twierdzenia o dwusiecznej mamy

Możemy zatem stąd podejrzewać, że chodzi o stosunek pól ścian tworzących kąt dwuścienny. Albo stosunek wysokości opuszczonych na wspólną krawędź – czy widzisz, Czytelniku, że to ta sama liczba?
Czyli udowodniliśmy już pierwszy ciekawy przypadek rozszerzonego twierdzenia:
Twierdzenie. Jeśli w czworościanie jedna z krawędzi jest prostopadła do pewnej ściany, to płaszczyzna dwusieczna kąta dwuściennego przy tej krawędzi dzieli przeciwległą krawędź w stosunku równym stosunkowi pól ścian zawierających krawędź tworzącą kąt dwuścienny.
Wydaje się, że takie twierdzenie może być prawdziwe dla dowolnego czworościanu, ale czy potrafimy to jakoś udowodnić?
Moglibyśmy złożyć dwa czworościany, które mają taką samą podstawę i które spełniają założenia opracowanego już szczególnego przypadku. Dokładniej, wysokości opuszczone na te ściany, które będziemy sklejać, muszą być krawędziami czworościanu.
Rys. 3
Czworościan
 możemy w ten sposób skleić z dwóch
mniejszych, gdy da się skonstruować płaszczyznę zawierającą pewną
krawędź i prostopadłą do krawędzi przeciwległej. Na rysunku 3 widać
płaszczyznę zawierającą krawędź
możemy w ten sposób skleić z dwóch
mniejszych, gdy da się skonstruować płaszczyznę zawierającą pewną
krawędź i prostopadłą do krawędzi przeciwległej. Na rysunku 3 widać
płaszczyznę zawierającą krawędź
 i prostopadłą do krawędzi
i prostopadłą do krawędzi
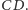 Punkt
Punkt
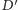 to punkt przecięcia tej płaszczyzny z krawędzią
to punkt przecięcia tej płaszczyzny z krawędzią
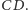
W tej sytuacji, korzystając ze szczególnego przypadku twierdzenia dla
czworościanów
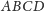 i
i
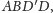 mamy
mamy

ponieważ odcinki
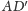 i
i
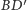 są prostopadłe do krawędzi
są prostopadłe do krawędzi
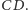 Co ciekawe, punkt
Co ciekawe, punkt
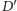 może leżeć też poza odcinkiem
może leżeć też poza odcinkiem
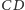 – wtedy można powiedzieć, że odejmujemy czworościany,
zamiast je dodawać.
– wtedy można powiedzieć, że odejmujemy czworościany,
zamiast je dodawać.
Niestety, to jeszcze nie wszystko. Istnieją czworościany
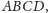 których
nie można w ten sposób skleić – spodki wysokości poprowadzonych
z wierzchołków
których
nie można w ten sposób skleić – spodki wysokości poprowadzonych
z wierzchołków
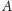 i
i
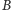 na prostą
na prostą
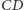 nie pokrywają się.
Co wtedy?
nie pokrywają się.
Co wtedy?
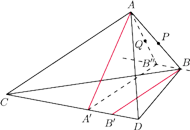
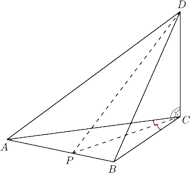
Rys. 4
Spróbujmy narysować sytuację dla dowolnego czworościanu (Rys. 4). Niech
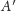 i
i
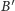 będą rzutami prostokątnymi odpowiednio wierzchołków
będą rzutami prostokątnymi odpowiednio wierzchołków
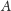 i
i
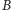 na prostą
na prostą
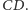 Umiemy już udowodnić twierdzenie
w przypadku, gdy punkty
Umiemy już udowodnić twierdzenie
w przypadku, gdy punkty
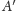 i
i
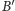 się pokrywają. Ogólnie jednak
nie musi tak być, więc nie mamy trójkąta, dla którego można by
zastosować twierdzenie o dwusiecznej.
się pokrywają. Ogólnie jednak
nie musi tak być, więc nie mamy trójkąta, dla którego można by
zastosować twierdzenie o dwusiecznej.
Skąd wziąć taki trójkąt? Może coś przesunąć tak, żeby punkty
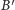 i
i
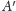 trafiły w jedno miejsce? Wyobraźmy sobie przesunięcie
równoległe odcinka
trafiły w jedno miejsce? Wyobraźmy sobie przesunięcie
równoległe odcinka
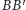 wzdłuż prostej
wzdłuż prostej
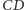 tak, żeby
tak, żeby
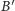 pokrył się z
pokrył się z
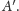 Niech
Niech
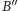 będzie obrazem punktu
będzie obrazem punktu
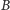 w tym przesunięciu.
w tym przesunięciu.
Wtedy punkt
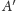 jest rzutem prostokątnym punktu
jest rzutem prostokątnym punktu
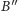 na prostą
na prostą
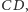 czyli czworościan
czyli czworościan
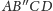 da się skleić z dwóch
„ładniejszych”, tak jak to robiliśmy przed chwilą! To znaczy, że jeśli
płaszczyzna dwusieczna kąta dwuściennego przy krawędzi
da się skleić z dwóch
„ładniejszych”, tak jak to robiliśmy przed chwilą! To znaczy, że jeśli
płaszczyzna dwusieczna kąta dwuściennego przy krawędzi
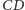 przecina
krawędź
przecina
krawędź
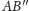 w punkcie
w punkcie
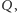 to
to

A ponieważ przesuwaliśmy punkt
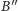 równolegle do
równolegle do
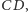 to
to
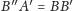 i
i
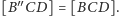 Gdybyśmy jeszcze wykazali,
że
Gdybyśmy jeszcze wykazali,
że

czyli inaczej, że proste
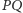 i
i
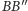 są równoległe, to
otrzymalibyśmy pełną wersję twierdzenia. Na szczęście to już jest łatwe:
skoro odcinki
są równoległe, to
otrzymalibyśmy pełną wersję twierdzenia. Na szczęście to już jest łatwe:
skoro odcinki
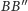 i
i
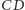 są równoległe, to każda płaszczyzna
zawierająca prostą
są równoległe, to każda płaszczyzna
zawierająca prostą
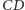 przecina płaszczyznę
przecina płaszczyznę
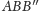 wzdłuż
pewnej prostej równoległej do
wzdłuż
pewnej prostej równoległej do
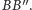 Zaraz, czy na pewno? Tak – gdyby
proste
Zaraz, czy na pewno? Tak – gdyby
proste
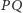 i
i
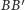 miały jakiś punkt wspólny
miały jakiś punkt wspólny
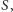 to
płaszczyzna dwusieczna kąta dwuściennego przy krawędzi
to
płaszczyzna dwusieczna kąta dwuściennego przy krawędzi
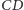 miałaby
trzy punkty wspólne z płaszczyzną
miałaby
trzy punkty wspólne z płaszczyzną
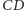 : punkty
: punkty
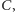
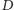 oraz
oraz
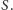 Wobec tego nie mamy już żadnych wątpliwości, że
Wobec tego nie mamy już żadnych wątpliwości, że
w dowolnym czworościanie płaszczyzna dwusieczna kąta dwuściennego dzieli przeciwległą krawędź w stosunku równym stosunkowi pól ścian czworościanu zawierających krawędź tego kąta dwuściennego.