Bryła ograniczona hiperboloidą jednopowłokową ma talię, ale nie jest wypukła.

Nasze bombki są kuliste – nie mają zaczepów, haczyków itp. Będziemy je wieszać za pomocą sztywnych obręczy z drutu w kształcie okręgu. Gdy bombkę uda się opasać obręczą w taki sposób, że nie można jej zsunąć, to cel będzie osiągnięty.

Niestety, bombce brakuje talii (jaką ma np. hiperboloida jednopowłokowa), wokół której da się ją skutecznie opasać. Możemy, oczywiście, wyciąć w bombce hiperboloidalną talię, nawet tak małą, że nikt ze świątecznych gości tego nie zauważy. Byłoby to jednak oszustwo, bo hiperboloidalna talia nie jest wypukła. Bombka z taką talią też by nie była, a na to nie chcemy się zgodzić!

Czy da się tak zdeformować bombkę, żeby pozostała wypukła i dała się skutecznie opasać? Czy istnieją wypukłe talie? Nie ufaj, Czytelniku, intuicji, jeśli podpowiada Ci, że nie, bo...

Talia może być wypukła

Do wykonania wypukłej talii potrzebne nam będzie potężne, ale proste w użyciu narzędzie teorii zbiorów wypukłych – operacja uwypuklenia, która każdemu zbiorowi 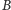 w przestrzeni przyporządkowuje zbiór 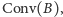 czyli najmniejszy zbiór wypukły zawierający 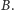 Uwypukleniem skończonego zbioru punktów jest wielościan (wypukły, oczywiście).

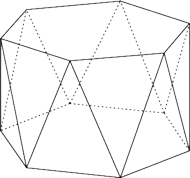
Antygraniastosłup ma talię i jest wypukły.

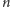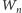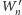
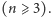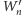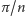Zbudujmy graniastosłup prawidłowy -kątny o podstawach  i Obróćmy podstawę  o kąt  wokół osi graniastosłupa, otrzymując wielokąt 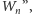 i przyjrzyjmy się zbiorowi 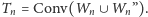 Otrzymaliśmy wielościan wypukły, którego ścianami bocznymi są trójkąty równoramienne. Jeśli ściany boczne są trójkątami równobocznymi, to wielościan jest antygraniastosłupem. Środki jego krawędzi bocznych są wierzchołkami 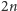-kąta foremnego i leżą wewnątrz walca wyznaczonego przez podstawy 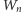 i 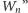 (dlaczego?), a zatem okrąg na nich opisany ma krótszy promień niż promienie okręgów opisanych na podstawach wielościanu. To zaś oznacza, że skonstruowaliśmy wypukłą talię!

Wykonanie wypukłej bombki z talią jest teraz proste. Wystarczy wyciąć jej cienki plasterek z okolic równika, umiejętnie wkleić w to miejsce odpowiednią talię i uwypuklić to, co powstało! Jeśli dobrze dobierzemy parametry talii (wysokość i głębokość wcięcia), to otrzymamy bryłę bardzo podobną do kuli. Będzie, co prawda, kanciasta, ale przecież nie można mieć (albo nie mieć) wszystkiego naraz...

A teraz... zagadka z niespodzianką

Przy konstrukcjach geometrycznych, w których występują sparametryzowane obiekty, warto się czasem zastanowić, co się stanie, gdy parametry przyjmą wartości graniczne. Np. co będzie, gdy okrąg skurczy się do punktu 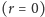lub się wyprostuje 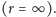W przypadku konstrukcji talii parametrem jest liczba  ( 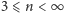) wierzchołków jej podstawy. Gdy 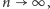 to talia 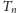 coraz bardziej przypomina walec i traci swoją taliowatość, by ją w granicy stracić całkowicie. Z tej strony zakresu parametrów nie znajdziemy nic ciekawego.

W talii 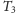 też nie ma nic szczególnego. Może się jednak zdarzyć, że stosunek długości krawędzi podstawy do krawędzi bocznej jest równy 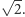 Dolepmy wtedy do podstaw ostrosłupy, których krawędzie boczne mają długość krawędzi bocznej talii. Otrzymany w ten sposób wielościan wypukły z talią widujesz, Czytelniku, codziennie. Co to za bryła?.

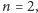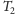To była zagadka, a gdzie jest niespodzianka? Żeby ją znaleźć, trzeba przekroczyć granicę. Wyobraźmy sobie, że  tzn. konstrukcję talii zaczynamy od „dwukątów” (czyli odcinków). Jeśli odległość odcinków dobraliśmy w taki sposób, że  jest antygraniastosłupem, to jest to wielościan wypukły z talią o sześciu krawędziach równej długości... Oto obiecana niespodzianka na Święta.