W czasie zawodów II stopnia uczniowie rozwiązywali pięć zadań, a my chcielibyśmy przedstawić rozwiązania jednego z nich.

Zadanie 5 miało treść następującą:

Nasuwa się pytanie, czy we wnętrzu podanego czworościanu dałoby się zmieścić więcej kul.

Okazuje się, że 4 kule umieszczone w narożach czworościanu jak w rozwiązaniu 1 oraz 6 kul z rozwiązania 2 nie mają punktów wspólnych. Łatwo zauważyć, że środki dwóch sąsiednich kul są środkami boków 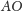i 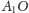w trójkącie 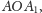a ich odległość jest równa 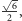czyli jest większa od 1.

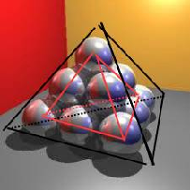
Zadanie z rozmieszczeniem 10 kul można również rozwiązać przez obliczenie wysokości czworościanu „opisanego” na piramidzie złożonej z 10 kul. Wystarczy zauważyć, że czworościan „opisany” na piramidzie jest obrazem czworościanu o krawędzi 2, którego wierzchołkami są środki czterech narożnych kul, w jednokładności o środku w punkcie przecięcia wysokości każdego z czworościanów. Wysokość takiego czworościanu wynosi 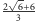i jest mniejsza od 4, czyli czworościan ten mieści się w czworościanie opisanym w treści zadania.

Zadanie z rozmieszczeniem 6 kul rozwiązało niewielu uczestników II etapu OMG. Można podejrzewać, że z rozwiązaniem zadania w wersji trudniejszej – o 10 kulach – poradziłoby sobie więcej osób, bo ustawienie tych kul w piramidę jest pomysłem naturalnym.