Ile jest wielościanów foremnych?
Pytanie postawione w tytule wydaje się dziwne. Przecież wiadomo co najmniej od czasów Platona, że wielościanów foremnych jest pięć typów: czworościan foremny, sześcian oraz ośmiościan, dwunastościan i dwudziestościan – wszystkie foremne. Łatwo też pokazuje się, że nie może być ich więcej. W czym zatem problem?

Rys. 1 Wielokąty gwiaździste.
Definiując i opisując wielościany foremne, zazwyczaj zakładamy milcząco, że są one wypukłe. A co będzie, gdy zrezygnujemy z wypukłości? Podobnie możemy zrezygnować z wypukłości ścian. Czy w takiej ogólniejszej sytuacji będziemy mogli mówić o wielościanach foremnych? Ile ich wtedy będzie?
Najpierw ustalmy pewne definicje. Zapewne pamiętamy, że wielokąt foremny to jest taki wielokąt wypukły, który ma wszystkie boki równe i kąty wewnętrzne przy wierzchołkach takie same, czyli przystające. Opuszczając słowo „wypukły” i nie zwracając uwagi na przecięcia boków, dostajemy określenie wielokąta foremnego gwiaździstego. Takie wielokąty powstają z przekątnych zwykłych wielokątów wypukłych. Najprostszy tworzą przekątne wypukłego pięciokąta foremnego – jest to pięciokąt gwiaździsty, czyli znany Pitagorejczykom pentagram. Przekątne sześciokąta nie zamykają się w wielokąt gwiaździsty – tu dostajemy kompozycje dwóch trójkątów równobocznych nazywaną często gwiazdą Dawida. Za to w siedmiokącie foremnym mamy aż dwa siedmiokąty gwiaździste.
Jeśli wielokąt foremny (gwiaździsty lub nie) ma
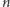 boków, a punkt
boków, a punkt
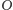 oznacza jego środek (czyli np. środek okręgu opisanego na tym
wielokącie), to punkt poruszający się po bokach wielokąta obiegnie środek
oznacza jego środek (czyli np. środek okręgu opisanego na tym
wielokącie), to punkt poruszający się po bokach wielokąta obiegnie środek
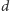 razy. Gdy wielokąt jest wypukły, to
razy. Gdy wielokąt jest wypukły, to
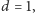 dla pentagramu
dla pentagramu
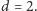 Kąt środkowy, czyli kąt o wierzchołku
Kąt środkowy, czyli kąt o wierzchołku
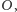 którego
ramiona przechodzą przez końce jednego boku, ma miarę
którego
ramiona przechodzą przez końce jednego boku, ma miarę
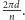 Liczbę
Liczbę
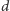 często nazywa się gęstością wielokąta foremnego. Liczby
często nazywa się gęstością wielokąta foremnego. Liczby
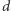 i
i
 są względnie pierwsze oraz
są względnie pierwsze oraz
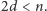 Wielokąt o
Wielokąt o
 bokach
i gęstości
bokach
i gęstości
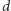 oznacza się symbolem
oznacza się symbolem
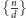 – jest to symbol
Schläfliego wielokąta foremnego.
– jest to symbol
Schläfliego wielokąta foremnego.
Można spróbować również rozszerzyć definicję wielościanu foremnego, rezygnując z wypukłości i dopuszczając ściany gwiaździste. Wielościan nazwiemy foremnym, gdy jego ściany są przystającymi wielokątami foremnymi, również gwiaździstymi, a w każdym wierzchołku schodzi się jednakowa liczba ścian. W takim przypadku, podobnie jak dla wielokątów gwiaździstych, ściany będą mogły się przenikać. Warto może zaznaczyć, że termin „ściana” jest tu już nieco umowny.
Wygodnie jest też zdefiniować wielościan foremny, używając pojęcia figury (wielokąta) wierzchołkowej. Figura wierzchołkowa jest wielokątem, którego wierzchołki są środkami krawędzi schodzących się w danym wierzchołku wielościanu. Dla sześcianu, na przykład, figurą wierzchołkową jest trójkąt, a dla dwudziestościanu pięciokąt.
Łatwo sprawdzamy, że wielościan jest foremny, gdy wszystkie ściany są
przystającymi wielokątami foremnymi i podobny warunek spełniają figury
wierzchołkowe. Dla wielościanów foremnych wprowadzamy również symbol
Schläfliego
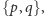 gdzie
gdzie
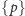 jest symbolem ściany, a
jest symbolem ściany, a
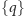 symbolem figury wierzchołkowej. Liczba
symbolem figury wierzchołkowej. Liczba
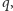 gdy jest całkowita, jest
także liczbą krawędzi lub, co na jedno wychodzi, ścian schodzących się
w wierzchołku wielościanu. Tak więc, np.
gdy jest całkowita, jest
także liczbą krawędzi lub, co na jedno wychodzi, ścian schodzących się
w wierzchołku wielościanu. Tak więc, np.
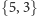 oznacza wielościan,
którego ścianami są pięciokąty, a figurami wierzchołkowymi trójkąty, czyli
w każdym wierzchołku tego wielościanu mamy trzy krawędzie. Jest to
naturalnie dwunastościan foremny.
oznacza wielościan,
którego ścianami są pięciokąty, a figurami wierzchołkowymi trójkąty, czyli
w każdym wierzchołku tego wielościanu mamy trzy krawędzie. Jest to
naturalnie dwunastościan foremny.
Jakie pary liczb
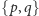 można przypisać wielościanom foremnym?
Klasyczne twierdzenie mówi, że dla wielościanów wypukłych dopuszczalne
są następujące symbole
można przypisać wielościanom foremnym?
Klasyczne twierdzenie mówi, że dla wielościanów wypukłych dopuszczalne
są następujące symbole
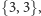
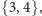
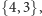
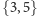 i
i
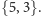 Z każdym związany jest pewien wielościan foremny. Jaki?
Czytelnik z pewnością sam zgadnie. Czy liczby
Z każdym związany jest pewien wielościan foremny. Jaki?
Czytelnik z pewnością sam zgadnie. Czy liczby
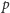 i
i
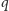 mogą
przyjmować wartości ułamkowe? Kepler na początku XVII, a Poinsot
na początku XIX wieku skonstruowali takie przykłady.
mogą
przyjmować wartości ułamkowe? Kepler na początku XVII, a Poinsot
na początku XIX wieku skonstruowali takie przykłady.
Jeśli w pięciokącie foremnym przedłużymy krawędzie aż do przecięcia,
to otrzymamy pięciokąt gwiaździsty. Możemy tak postąpić z każdym
pięciokątem – ścianą dwunastościanu foremnego. Otrzymamy wtedy obiekt
nazywany dwunastościanem gwiaździstym małym. Jego ścianami są
pentagramy i w każdym wierzchołku schodzi się ich pięć, a zatem spełnione
są warunki rozszerzonej definicji wielościanu foremnego. Zgodnie z przyjętymi
zasadami jego symbol ma postać
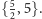
Rys. 2 Dwunastościan gwiaździsty mały i idea konstrukcji
Istnienie wielościanu o symbolu
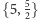 udowodnił Poinsot. Wystarczy
w każdym pentagramie dwunastościanu gwiaździstego małego połączyć
wierzchołki, tworząc ponownie wypukłe pięciokąty foremne. Powstały
wielościan jest figurą niezwykłą, gdyż zbudowany jest, podobnie jak
dwunastościan foremny, z dwunastu pięciokątów, a jego figurą wierzchołkową
jest pentagram. Nazwano go dwunastościanem wielkim.
udowodnił Poinsot. Wystarczy
w każdym pentagramie dwunastościanu gwiaździstego małego połączyć
wierzchołki, tworząc ponownie wypukłe pięciokąty foremne. Powstały
wielościan jest figurą niezwykłą, gdyż zbudowany jest, podobnie jak
dwunastościan foremny, z dwunastu pięciokątów, a jego figurą wierzchołkową
jest pentagram. Nazwano go dwunastościanem wielkim.
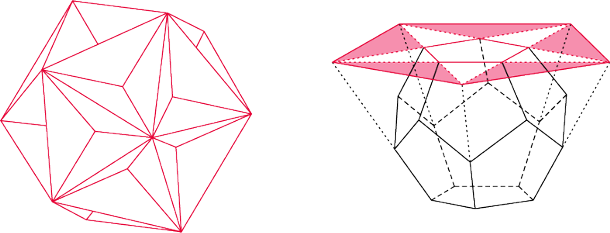
Rys. 3 Dwunastościan gwiaździsty wielki i idea konstrukcji
Jeśli w dwudziestościanie foremnym poprowadzimy płaszczyzny tak, że będą zawierały podstawy ostrosłupów pięciokątnych, to utworzą one właśnie dwunastościan wielki.
Czy można wskazać jeszcze jakieś inne niewypukłe wielościany foremne? Kepler i Poinsot skonstruowali jeszcze po jednym, a Poinsot zastanawiał się, czy to już wszystkie możliwości. No właśnie, jak sprawdzić, czy przypadkiem czegoś nie przeoczono? O ile dla wielościanów wypukłych łatwo przekonujemy się, że więcej możliwości być nie może (wystarczy sprawdzić, ile wielokątów foremnych i jakie mogą się schodzić w jednym wierzchołku), o tyle, gdy rezygnujemy z wypukłości, sprawa staje się dużo trudniejsza.
Z pomocą przychodzą wiadomości dotyczące izometrii własnych figur (symetrii figur) i ich grup. Przypomnijmy, że izometrią własną albo symetrią figury nazywamy taką izometrię, która przekształca figurę na siebie. Może to być obrót, symetria osiowa, symetria płaszczyznowa (odbicie), a także przekształcenie identycznościowe. Nietrudno się przekonać, że symetrie figury tworzą grupę: złożenie dwóch symetrii jest symetrią i przekształcenie odwrotne do symetrii figury też jest jej symetrią. Na przykład: czworościan foremny ma 24 symetrie – każdej jednoznacznie odpowiada jakaś permutacja wierzchołków.
Dla nas będzie interesujące pewne ważne twierdzenie dotyczące, między innymi,
obrotów własnych wielościanów foremnych. Zanim je sformułujemy,
przypomnijmy, że każdy obrót na płaszczyźnie wykonujemy wokół
pewnego punktu – środka obrotu, a obrót w przestrzeni dokoła pewnej
prostej – osi. Jeśli obrót o kąt
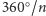 jest obrotem własnym figury, to
mówimy, że figura ma
jest obrotem własnym figury, to
mówimy, że figura ma
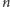 -krotny środek obrotu lub
-krotny środek obrotu lub
 -krotną oś
obrotu w zależności od typu obrotu. Na przykład: pięciokąt foremny ma
pięciokrotny środek obrotu, a czworościan foremny ma trzykrotne osie
obrotu, ale ma też dwukrotne osie obrotu (czyli osie symetrii) przechodzące
przez środki krawędzi skośnych.
-krotną oś
obrotu w zależności od typu obrotu. Na przykład: pięciokąt foremny ma
pięciokrotny środek obrotu, a czworościan foremny ma trzykrotne osie
obrotu, ale ma też dwukrotne osie obrotu (czyli osie symetrii) przechodzące
przez środki krawędzi skośnych.
Oto treść sygnalizowanego twierdzenia
Twierdzenie. Jeśli grupa obrotów w przestrzeni jest skończona i zawiera
co najmniej dwa obroty różne od obrotów o
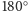 i o różnych osiach,
to jest identyczna (izomorficzna) z jedną z trzech następujących grup:
i o różnych osiach,
to jest identyczna (izomorficzna) z jedną z trzech następujących grup:
- grupą obrotów czworościanu foremnego,
- grupą obrotów sześcianu (i tym samym ośmiościanu foremnego),
- grupą obrotów dwunastościanu foremnego (identyczną z grupą obrotów dwudziestościanu foremnego).
Niestety, nie ma tu miejsca na dowód tego ważnego faktu. Czytelnik zainteresowany dowodem może go znaleźć, na przykład, w klasycznej książce Hermana Weyla „Symetria”.
Zobaczmy, jak to twierdzenie pozwala wyznaczyć niewypukłe wielościany
foremne. Każdy z wielościanów foremnych o symbolu
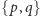 musi
mieć jedną z trzech wymienionych w twierdzeniu grup obrotów własnych.
Wygodnie jest zrzutować powierzchnię wielościanu na powierzchnię
sfery stycznej do wszystkich ścian wielościanu (sfery wpisanej) – rzut
wykonujemy ze środka sfery. Dzięki temu wystarczy studiować odpowiednie
mozaiki na sferze i ich obroty. Zauważmy jeszcze, że w grupie symetrii
podziału sfery odpowiadającego wielościanowi
musi
mieć jedną z trzech wymienionych w twierdzeniu grup obrotów własnych.
Wygodnie jest zrzutować powierzchnię wielościanu na powierzchnię
sfery stycznej do wszystkich ścian wielościanu (sfery wpisanej) – rzut
wykonujemy ze środka sfery. Dzięki temu wystarczy studiować odpowiednie
mozaiki na sferze i ich obroty. Zauważmy jeszcze, że w grupie symetrii
podziału sfery odpowiadającego wielościanowi
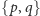 mamy obroty
o
mamy obroty
o
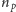 -krotnych środkach pokrywających się ze środkami ścian oraz
-krotnych środkach pokrywających się ze środkami ścian oraz
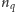 -krotne obroty o środkach w wierzchołkach. Liczby
-krotne obroty o środkach w wierzchołkach. Liczby
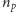 i
i
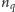 są ewentualnie licznikami liczb
są ewentualnie licznikami liczb
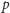 i
i
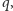 gdy są one
ułamkami.
gdy są one
ułamkami.

Rys. 5
Z cytowanego twierdzenia wynika, że jeśli szukamy wielościanu foremnego
różnego od znanych brył platońskich o symbolu
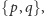 to jego grupa
symetrii musi być grupą obrotów dwunastościanu foremnego, która jako
jedyna ma pięciokrotne osie obrotu, co gwarantuje pięciokrotne środki obrotu
dla odpowiadającego podziału sfery. Zatem wielościany foremne niewypukłe
mogą mieć tylko symbole
to jego grupa
symetrii musi być grupą obrotów dwunastościanu foremnego, która jako
jedyna ma pięciokrotne osie obrotu, co gwarantuje pięciokrotne środki obrotu
dla odpowiadającego podziału sfery. Zatem wielościany foremne niewypukłe
mogą mieć tylko symbole
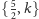 względnie
względnie
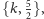 gdzie
gdzie
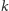 może przyjąć wyłącznie jedną z trzech wartości: 3, 5 albo
może przyjąć wyłącznie jedną z trzech wartości: 3, 5 albo
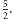
Ostatnią wartość da się wyeliminować. Przyjrzyjmy się temu bliżej.
Porównamy podział sfery dla hipotetycznego wielościanu
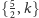 z podziałem dla dwunastościanu foremnego.
z podziałem dla dwunastościanu foremnego.
Niech na sferze będzie dany podział typu
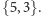 Wybierzmy jedną
ze ścian wraz ze sferycznym pięciokątem gwiaździstym
Wybierzmy jedną
ze ścian wraz ze sferycznym pięciokątem gwiaździstym
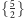 umieszczonym tak, żeby grupa obrotów dwunastościanu była dla niego grupą
symetrii. Ten pięciokąt może być umieszczony tylko na dwa sposoby, żeby
nie burzyć symetrii i żeby można było dołożyć kolejne pięciokąty
gwiaździste związane z potencjalnym wielościanem
umieszczonym tak, żeby grupa obrotów dwunastościanu była dla niego grupą
symetrii. Ten pięciokąt może być umieszczony tylko na dwa sposoby, żeby
nie burzyć symetrii i żeby można było dołożyć kolejne pięciokąty
gwiaździste związane z potencjalnym wielościanem
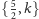 :
:
- wierzchołki pięciokąta gwiaździstego są środkami ścian przyległych do wyróżnionej;
- wierzchołki pięciokąta gwiaździstego są wierzchołkami ścian również przyległych do tej wybranej.
Znów powołując się na zachowanie symetrii, zauważamy, że w pierwszym
przypadku możemy otrzymać podział typu
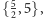 bo w środku
zejdzie się pięć pentagramów. Natomiast w drugim przypadku w wierzchołku
zejdą się tylko trzy pentagramy, czyli podział odpowiada
bo w środku
zejdzie się pięć pentagramów. Natomiast w drugim przypadku w wierzchołku
zejdą się tylko trzy pentagramy, czyli podział odpowiada
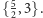 Dzięki dwoistości możliwe są jeszcze tylko podziały:
Dzięki dwoistości możliwe są jeszcze tylko podziały:
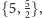
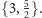

Rys. 6a
Ostatecznie więc, możliwe są co najwyżej cztery niewypukłe wielościany foremne, czyli Kepler i Poinsot znaleźli wszystkie dopuszczalne obiekty.
Pierwszym, który udowodnił, że są tylko cztery wielościany foremne niewypukłe, był Augustyn Cauchy. Posłużył się on również własnościami rzutu powierzchni wielościanu na sferę i wykorzystał pewne pomysły Poinsota. Nie znał on naturalnie twierdzenia o klasyfikacji grup obrotów w przestrzeni.
Na koniec opiszemy krótko, jak można skonstruować dwunastościan gwiaździsty wielki i dwudziestościan wielki. Pierwszy z nich otrzymamy z dwunastościanu wielkiego przez przedłużanie krawędzi – boków pięciokątów. Jak już wiemy, przedłużając boki pięciokąta foremnego, otrzymamy pentagram. W omawianym przypadku trzy pentagramy zejdą się w jednym wierzchołku, tworząc dwunastościan gwiaździsty wielki.
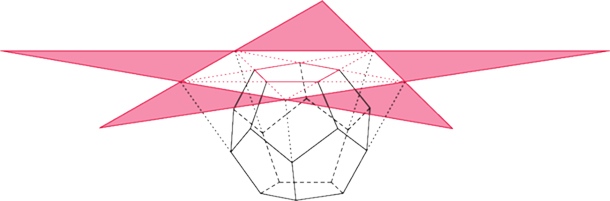
Rys. 6b

Rys. 7a
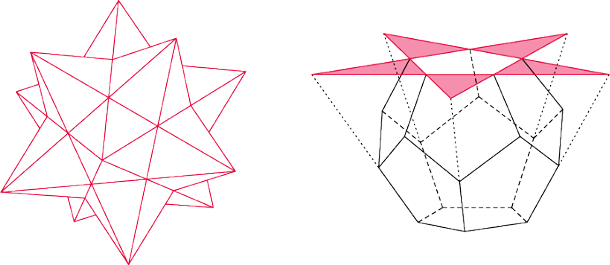
Konstrukcja dwudziestościanu wielkiego jest bardziej skomplikowana.
Umieśćmy dwudziestościan foremny na płaszczyźnie tak, żeby jedna
z jego ścian leżała na tej płaszczyźnie. Przyjrzyjmy się teraz ścianie
przeciwległej. Przez przyległe do niej trójkąty poprowadźmy płaszczyzny.
Wyznaczą one na pierwszej płaszczyźnie trójkąt równoboczny – jest to
ściana dwudziestościanu wielkiego. Powtarzając procedurę dla każdej
ze ścian dwudziestościanu foremnego, otrzymamy dwudziestościan wielki –
foremny wielościan niewypukły zbudowany również z dwudziestu
trójkątów równobocznych. Jego symbol Schläfliego to właśnie
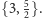
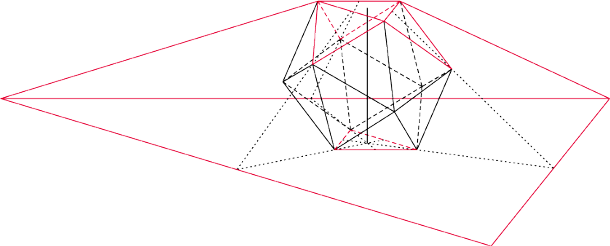
Rys. 7b
Czytelnicy pragnący wykonać modele omawianych wielościanów znajdą ich opis w książce H.M. Cundy, A.P. Rollett Modele matematyczne.
Podobnie możemy zapytać o niewypukłe wielościany archimedesowe. Tu sprawa jest jeszcze bardziej skomplikowana i ostateczny wynik uzyskano dopiero w latach siedemdziesiątych XX wieku.