Przy rozwiązywaniu zadań dotyczących tego tematu należy jedynie pamiętać o tym, że

•

jeśli dwie nierównoległe proste leżące w jednej płaszczyźnie są prostopadłe do trzeciej prostej, to cała płaszczyzna też jest prostopadła do niej;

•

jeśli prosta jest prostopadła do pewnej płaszczyzny, to jest prostopadła do dowolnej prostej leżącej w tej płaszczyźnie.

I to jest cała filozofia – wszystkie zadania o prostopadłości rozwiązuje się, posługując się tym schematem. Czasem należy tylko umieć wybrać, czy wygodniej będzie wykazać, że, na przykład, rzut prostokątny punktu 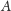na płaszczyznę spełnia jakieś warunki, czy odwrotnie – wziąć punkt na tej płaszczyźnie spełniający dane warunki i pokazać, że prosta łącząca go z punktem 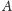jest prostopadła do tej płaszczyzny. Przy odrobinie praktyki jednak szybko nabierzemy wyczucia. Zacznijmy od prostego, ale bardzo użytecznego zadania.

Warto ten fakcik sobie zapamiętać, bo nie raz dane nam będzie z niego skorzystać. Przejdźmy teraz do nieco trudniejszego zadania, w którym zobaczymy, jak wykorzystać prostopadłość prostych skośnych.

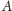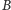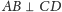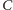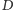Okazuje się w takim razie, że nie w każdym czworościanie istnieje punkt przecięcia wszystkich wysokości. Z naszego rozwiązania wynika bowiem, że wysokości poprowadzone z wierzchołków  i  przecinają się wtedy i tylko wtedy, gdy (z uwagi na symetrię dotyczy to również wysokości poprowadzonych z punktów  i  ). Czworościany, w których wszystkie wysokości przecinają się w jednym punkcie, nazywamy ortocentrycznymi, ale o nich następnym razem.

Do samodzielnego rozwiązania

I na koniec całe mnóstwo zadań dodatkowych.