Klub 44F - zadania VI 2020»Zadanie 700
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania VI 2020
- Publikacja w Delcie: czerwiec 2020
- Publikacja elektroniczna: 31 maja 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (431 KB)
Jedna okładka powietrznego kondensatora płaskiego o pojemności  jest nienaładowana, druga jest naładowana ładunkiem
jest nienaładowana, druga jest naładowana ładunkiem 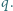 Okładki połączono przewodnikiem o dużym oporze. Ile ciepła wydzieli się w przewodniku po długim czasie? Rozmiary okładek kondensatora są bardzo duże w porównaniu z odległością między nimi.
Okładki połączono przewodnikiem o dużym oporze. Ile ciepła wydzieli się w przewodniku po długim czasie? Rozmiary okładek kondensatora są bardzo duże w porównaniu z odległością między nimi.
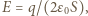
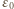
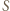
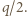
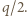
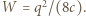
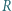 i
i 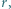 naładowanych odpowiednio ładunkami
naładowanych odpowiednio ładunkami 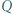 i
i 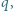 rozłożonymi równomiernie na powierzchniach półsfer. Środki półsfer oraz płaszczyzny ich maksymalnych przekrojów pokrywają się.
rozłożonymi równomiernie na powierzchniach półsfer. Środki półsfer oraz płaszczyzny ich maksymalnych przekrojów pokrywają się.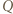 i
i 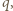 co nie zmniejsza ogólności rozwiązania.
co nie zmniejsza ogólności rozwiązania.
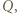 to siła działająca na półsferę o promieniu
to siła działająca na półsferę o promieniu  będzie równa zeru, bo wewnątrz naładowanej sfery nie ma pola elektrycznego. Zatem półsfery o promieniach
będzie równa zeru, bo wewnątrz naładowanej sfery nie ma pola elektrycznego. Zatem półsfery o promieniach 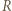 działają na małą półsferę siłami, które się równoważą.
działają na małą półsferę siłami, które się równoważą.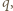 jak na
jak na 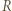 będzie działała siła
będzie działała siła 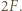
 naładowanej ładunkiem
naładowanej ładunkiem 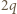 w odległości
w odległości 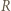 od jej środka ma wartość
od jej środka ma wartość 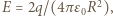 gdzie
gdzie 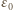 jest przenikalnością elektryczną próżni. Ciśnienie na dużą półsferę wynosi
jest przenikalnością elektryczną próżni. Ciśnienie na dużą półsferę wynosi 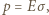 gdzie
gdzie 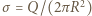 jest gęstością powierzchniową ładunku. Zatem siła działająca na dużą półsferę ze strony małej sfery dana jest wzorem
jest gęstością powierzchniową ładunku. Zatem siła działająca na dużą półsferę ze strony małej sfery dana jest wzorem 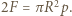
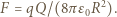
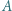 kondensatora cylindrycznego wylatuje lekko rozchodząca się wiązka jonów dodatnich. Kąt rozwarcia wiązki wynosi
kondensatora cylindrycznego wylatuje lekko rozchodząca się wiązka jonów dodatnich. Kąt rozwarcia wiązki wynosi 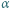 (
(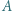 jest prostopadła do odcinka
jest prostopadła do odcinka 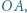 poruszają się po okręgu o promieniu
poruszają się po okręgu o promieniu 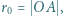 współśrodkowym z okładkami kondensatora. Pokazać, że wiązka jonów ponownie zogniskuje się w pewnym punkcie
współśrodkowym z okładkami kondensatora. Pokazać, że wiązka jonów ponownie zogniskuje się w pewnym punkcie 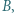 i znaleźć kąt
i znaleźć kąt 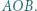 Wyznaczyć maksymalną szerokość wiązki.
Wyznaczyć maksymalną szerokość wiązki.


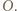 Z prawa Gaussa wartość natężenia pola
Z prawa Gaussa wartość natężenia pola 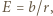 gdzie
gdzie  jest odległością od punktu
jest odległością od punktu 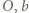 stałą proporcjonalności. Przyspieszenie dośrodkowe jonu poruszającego się po orbicie o promieniu
stałą proporcjonalności. Przyspieszenie dośrodkowe jonu poruszającego się po orbicie o promieniu 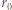 wywołane jest siłą
wywołane jest siłą 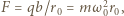 stąd prędkość kątowa jonu
stąd prędkość kątowa jonu 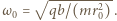
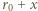 od środka okręgu O działa w układzie wirującym wokół osi kondensatora siła
od środka okręgu O działa w układzie wirującym wokół osi kondensatora siła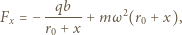
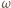 jest prędkością kątową jonu i możemy ją otrzymać z zasady zachowania momentu pędu:
jest prędkością kątową jonu i możemy ją otrzymać z zasady zachowania momentu pędu: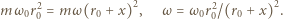
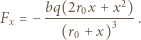
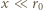
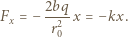
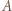 tworzy mały kąt z prędkością jonów na podstawowej orbicie, wykonują radialne drgania harmoniczne o okresie
tworzy mały kąt z prędkością jonów na podstawowej orbicie, wykonują radialne drgania harmoniczne o okresie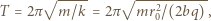
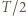 wszystkie jony, które wystartowały w punkcie
wszystkie jony, które wystartowały w punkcie 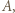 spotkają się w jednym punkcie
spotkają się w jednym punkcie 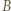 orbity podstawowej. Szukany kąt
orbity podstawowej. Szukany kąt 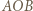 ma wartość
ma wartość 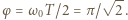
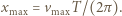 W naszym przypadku
W naszym przypadku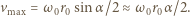
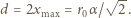
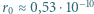 m? Masa elektronu
m? Masa elektronu 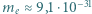
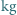 , stała Plancka
, stała Plancka 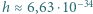 Js, ładunek elementarny
Js, ładunek elementarny 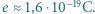
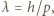 gdzie
gdzie 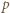 jest pędem cząstki. Energie kinetyczne elektronów w rozważanych procesach są małe w porównaniu z energią spoczynkową elektronu (
jest pędem cząstki. Energie kinetyczne elektronów w rozważanych procesach są małe w porównaniu z energią spoczynkową elektronu ( 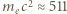 keV), możemy więc użyć klasycznego związku pędu i energii kinetycznej cząstki. Energia kinetyczna uzyskana przez elektron przyspieszany napięciem
keV), możemy więc użyć klasycznego związku pędu i energii kinetycznej cząstki. Energia kinetyczna uzyskana przez elektron przyspieszany napięciem 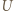 wynosi:
wynosi: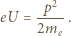
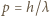 otrzymujemy:
otrzymujemy: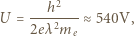

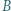 , toczy się bez poślizgu z prędkością
, toczy się bez poślizgu z prędkością  cienki metalowy pierścień, w którym jest bardzo mała przerwa o długości
cienki metalowy pierścień, w którym jest bardzo mała przerwa o długości 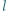 . Wektor
. Wektor 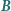 jest prostopadły do płaszczyzny pierścienia. Znaleźć SEM indukcji w chwili, gdy promień pierścienia trafiający w rozcięcie tworzy z pionem kąt
jest prostopadły do płaszczyzny pierścienia. Znaleźć SEM indukcji w chwili, gdy promień pierścienia trafiający w rozcięcie tworzy z pionem kąt 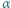 .
.
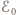 w przerwanym pierścieniu spełnia równanie
w przerwanym pierścieniu spełnia równanie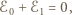
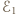 jest siłą elektromotoryczną, jaka powstaje w elemencie o długości
jest siłą elektromotoryczną, jaka powstaje w elemencie o długości 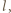 uzupełniającym przerwę w pierścieniu. Prędkość
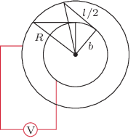
uzupełniającym przerwę w pierścieniu. Prędkość  tego elementu jest sumą prędkości ruchu postępowego i obrotowego (rysunek obok) i ma wartość
tego elementu jest sumą prędkości ruchu postępowego i obrotowego (rysunek obok) i ma wartość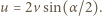
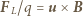
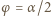 ze styczną do pierścienia. Siła elektromotoryczna
ze styczną do pierścienia. Siła elektromotoryczna 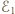 jest pracą wykonaną przez siłę Lorentza nad jednostkowym ładunkiem na drodze
jest pracą wykonaną przez siłę Lorentza nad jednostkowym ładunkiem na drodze 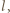 zatem
zatem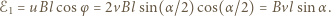
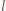 rośnie w kierunku zgodnym ze wskazówkami zegara. Szukana siła elektromotoryczna indukcji w rozerwanym pierścieniu dana jest wzorem
rośnie w kierunku zgodnym ze wskazówkami zegara. Szukana siła elektromotoryczna indukcji w rozerwanym pierścieniu dana jest wzorem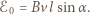
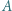 i
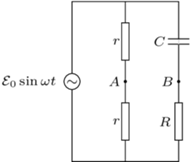
i 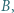 w obwodzie przedstawionym na, od oporu
w obwodzie przedstawionym na, od oporu 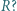
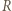 jest równe
jest równe 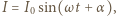 gdzie
gdzie 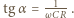

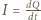 otrzymujemy napięcie na kondensatorze
otrzymujemy napięcie na kondensatorze 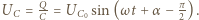 Jest ono przesunięte w fazie o kąt
Jest ono przesunięte w fazie o kąt 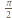 względem napięcia na oporniku
względem napięcia na oporniku 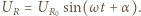
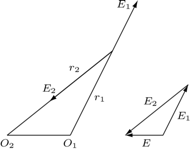
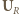 oraz
oraz 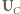 są prostopadłe, a ich suma jest wektorem o wartości
są prostopadłe, a ich suma jest wektorem o wartości 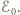 Napięcie na każdym z oporników
Napięcie na każdym z oporników  wynosi
wynosi 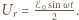 Wektor napięcia między punktami
Wektor napięcia między punktami  i
i 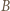 dany jest wzorem
dany jest wzorem 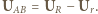 Z rysunku widać, że szukana amplituda tego napięcia jest promieniem okręgu opisanego na trójkącie prostokątnym, którego przeciwprostokątna wynosi
Z rysunku widać, że szukana amplituda tego napięcia jest promieniem okręgu opisanego na trójkącie prostokątnym, którego przeciwprostokątna wynosi 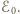 Zatem
Zatem 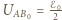 i nie zależy od wartości oporu
i nie zależy od wartości oporu 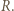
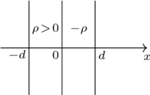
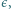 naładowanych z gęstościami objętościowymi
naładowanych z gęstościami objętościowymi 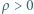 i
i 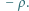 Grubość każdej warstwy wynosi
Grubość każdej warstwy wynosi 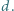 Przyjąć warunek brzegowy dla potencjału
Przyjąć warunek brzegowy dla potencjału 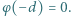
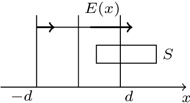
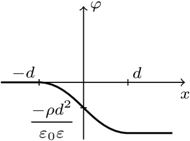
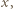 a natężenie pola elektrycznego ma największą wartość dla
a natężenie pola elektrycznego ma największą wartość dla 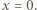 Stosując prawo Gaussa dla powierzchni zamkniętej w kształcie prostopadłościanu, którego przekrój przedstawiony jest na rysunku 1, a powierzchnia podstawy wynosi
Stosując prawo Gaussa dla powierzchni zamkniętej w kształcie prostopadłościanu, którego przekrój przedstawiony jest na rysunku 1, a powierzchnia podstawy wynosi 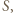 otrzymujemy równanie:
otrzymujemy równanie: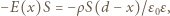
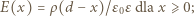
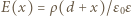 dla
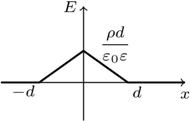
dla 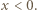 Zależność wartości wektora natężenia pola elektrycznego od współrzędnej
Zależność wartości wektora natężenia pola elektrycznego od współrzędnej  przedstawia wykres na rysunku 2. Różnica potencjałów między dwoma punktami równa jest pracy pola elektrycznego nad jednostkowym ładunkiem, wziętej ze znakiem minus. Pracę tę możemy policzyć jako pole pod wykresem na rysunku 3.
przedstawia wykres na rysunku 2. Różnica potencjałów między dwoma punktami równa jest pracy pola elektrycznego nad jednostkowym ładunkiem, wziętej ze znakiem minus. Pracę tę możemy policzyć jako pole pod wykresem na rysunku 3.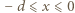 mamy:
mamy: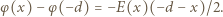
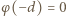 otrzymujemy:
otrzymujemy: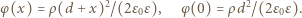
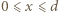 otrzymujemy:
otrzymujemy: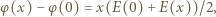
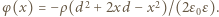 Wykres funkcji
Wykres funkcji 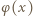 przedstawiony jest na rysunku 3.
przedstawiony jest na rysunku 3.
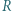 jest dużo większy niż opór wewnętrzny ogniwa:
jest dużo większy niż opór wewnętrzny ogniwa: 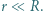 Podłączenie woltomierza o oporze
Podłączenie woltomierza o oporze 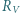 powoduje zmianę napięcia między punktami
powoduje zmianę napięcia między punktami 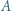 i
i 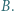 Jaka powinna być relacja między oporami
Jaka powinna być relacja między oporami 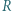 i
i 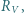 aby to zaburzenie było jak najmniejsze?
aby to zaburzenie było jak najmniejsze?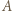 i
i 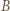 wynosi
wynosi 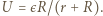 Po podłączeniu
Po podłączeniu 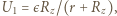 gdzie
gdzie 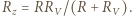 Podłączenie woltomierza powoduje wzrost natężenia prądu płynącego przez źródło, co pociąga za sobą wzrost napięcia na oporze wewnętrznym źródła i obniżenie napięcia między punktami
Podłączenie woltomierza powoduje wzrost natężenia prądu płynącego przez źródło, co pociąga za sobą wzrost napięcia na oporze wewnętrznym źródła i obniżenie napięcia między punktami 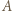 i
i 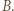 Zachodzi relacja
Zachodzi relacja 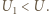 Względne zaburzenie napięcia między punktami
Względne zaburzenie napięcia między punktami 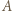 i
i 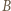 wynosi
wynosi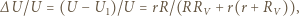
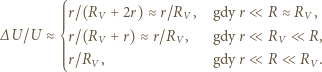
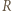 i
i 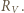
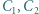 i
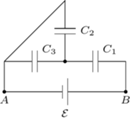
i 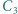 oraz ogniwo o sile elektromotorycznej
oraz ogniwo o sile elektromotorycznej 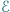 połączono jak na rysunku obok. Jakie ładunki zgromadziły się na poszczególnych kondensatorach? Ile wynosi pojemność zastępcza
połączono jak na rysunku obok. Jakie ładunki zgromadziły się na poszczególnych kondensatorach? Ile wynosi pojemność zastępcza 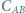 między punktami
między punktami 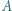 i
i 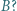
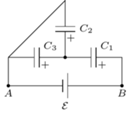
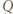 i napięcia
i napięcia 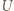 na kondensatorach tak jak ich pojemności.
na kondensatorach tak jak ich pojemności.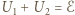 oraz
oraz 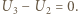 Zauważmy, że elektrody "dodatnie" kondensatorów
Zauważmy, że elektrody "dodatnie" kondensatorów 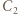 i
i 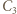 oraz elektroda "ujemna"
oraz elektroda "ujemna" 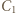 są połączone, a więc tworzą jeden przewodnik. W związku z tym ładunki na nich mogły zgromadzić się wyłącznie w wyniku rozdzielenia i przemieszczenia ładunków tego przewodnika. Ponieważ nie jest on połączony z żadnym z biegunów baterii, to całkowity ładunek na nim musi być równy zeru - to także wniosek z prawa Kirchhoffa dla sumy prądów w węzłach sieci. Mamy więc
są połączone, a więc tworzą jeden przewodnik. W związku z tym ładunki na nich mogły zgromadzić się wyłącznie w wyniku rozdzielenia i przemieszczenia ładunków tego przewodnika. Ponieważ nie jest on połączony z żadnym z biegunów baterii, to całkowity ładunek na nim musi być równy zeru - to także wniosek z prawa Kirchhoffa dla sumy prądów w węzłach sieci. Mamy więc 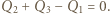 Pamiętając, że dla każdego z kondensatorów
Pamiętając, że dla każdego z kondensatorów 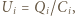 otrzymujemy układ równań:
otrzymujemy układ równań: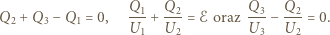
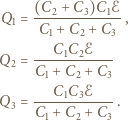
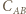 otrzymamy, dzieląc sumę ładunków na okładkach połączonych z punktem
otrzymamy, dzieląc sumę ładunków na okładkach połączonych z punktem 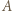 przez siłę elektromotoryczną
przez siłę elektromotoryczną 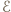 (potencjał punktu
(potencjał punktu  ):
):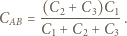
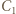 połączony szeregowo z równolegle połączonymi kondensatorami
połączony szeregowo z równolegle połączonymi kondensatorami 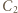 i
i 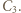
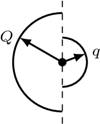
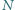 cząsteczek, z których każda ma moment dipolowy
cząsteczek, z których każda ma moment dipolowy 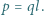 Odległość
Odległość 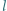 między ładunkami dipola jest dużo mniejsza od promienia kuli.
między ładunkami dipola jest dużo mniejsza od promienia kuli.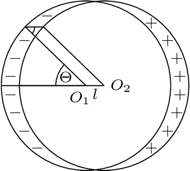
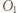 znajdują się ładunki ujemne, wewnątrz kuli o środku w punkcie
znajdują się ładunki ujemne, wewnątrz kuli o środku w punkcie 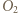 ładunki dodatnie. Gęstość objętościowa ładunków
ładunki dodatnie. Gęstość objętościowa ładunków 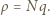 Odległość między środkami kul jest równa
Odległość między środkami kul jest równa 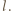 Natężenie pola w dowolnym punkcie w obszarze, w którym kule nachodzą na siebie, jest sumą wektorową natężeń od obu kul.
Natężenie pola w dowolnym punkcie w obszarze, w którym kule nachodzą na siebie, jest sumą wektorową natężeń od obu kul.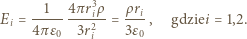
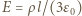 i zwrot przeciwny do wektora
i zwrot przeciwny do wektora 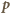
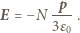
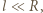 gdzie
gdzie 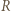 jest promieniem kuli, szukana gęstość ładunków powierzchniowych dana jest wzorem:
jest promieniem kuli, szukana gęstość ładunków powierzchniowych dana jest wzorem: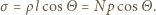
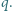 Powierzchnia okładek jest bardzo duża, efekty brzegowe możemy zaniedbać. Odległość ładunku od jednej z okładek jest równa
Powierzchnia okładek jest bardzo duża, efekty brzegowe możemy zaniedbać. Odległość ładunku od jednej z okładek jest równa 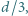 gdzie
gdzie 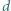 jest odległością między okładkami. Jaki ładunek przepłynie przez przewodnik zwierający okładki, gdy ładunek
jest odległością między okładkami. Jaki ładunek przepłynie przez przewodnik zwierający okładki, gdy ładunek 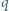 zostanie przesunięty w miejsce wewnątrz kondensatora, odległe o
zostanie przesunięty w miejsce wewnątrz kondensatora, odległe o 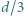 od drugiej okładki?
od drugiej okładki?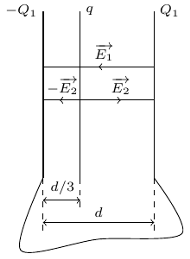
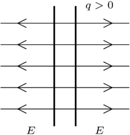
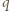 równolegle do okładek (zmienia się tylko ich rozkład). Oznacza to, że wartość ładunków indukowanych nie zmieni się również wtedy, gdy ładunek
równolegle do okładek (zmienia się tylko ich rozkład). Oznacza to, że wartość ładunków indukowanych nie zmieni się również wtedy, gdy ładunek 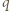 zostanie równomiernie "rozmazany" na powierzchni równoległej do okładek kondensatora (rysunek). Ładunki
zostanie równomiernie "rozmazany" na powierzchni równoległej do okładek kondensatora (rysunek). Ładunki 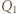 i
i 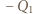 wytwarzają między okładkami kondensatora jednorodne pole o natężeniu
wytwarzają między okładkami kondensatora jednorodne pole o natężeniu 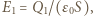 gdzie
gdzie 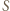 jest powierzchnią okładek. Płaszczyzna wewnątrz kondensatora naładowana ładunkiem
jest powierzchnią okładek. Płaszczyzna wewnątrz kondensatora naładowana ładunkiem 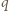 wytwarza pole o natężeniu
wytwarza pole o natężeniu 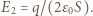 Napięcie między płaszczyzną naładowaną ładunkiem
Napięcie między płaszczyzną naładowaną ładunkiem 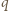 a lewą okładką wynosi
a lewą okładką wynosi 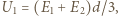 napięcie między tą samą płaszczyzną i prawą okładką
napięcie między tą samą płaszczyzną i prawą okładką 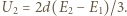 Jednocześnie napięcie między okładkami zwartego kondensatora wynosi 0, stąd
Jednocześnie napięcie między okładkami zwartego kondensatora wynosi 0, stąd 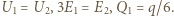 Analogicznie ładunek na prawej okładce po przesunięciu ładunku
Analogicznie ładunek na prawej okładce po przesunięciu ładunku 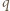 w położenie końcowe jest równy
w położenie końcowe jest równy 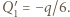 Szukany ładunek przepływający między okładkami kondensatora podczas przemieszczania ładunku punktowego
Szukany ładunek przepływający między okładkami kondensatora podczas przemieszczania ładunku punktowego 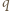 dany jest wzorem
dany jest wzorem 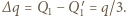
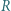 kulistego końca tego pręta, żeby po naładowaniu go do potencjału
kulistego końca tego pręta, żeby po naładowaniu go do potencjału 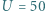 kV nie nastąpiło wyładowanie do atmosfery? Powietrze ulega przebiciu (jonizacji) w polu elektrycznym
kV nie nastąpiło wyładowanie do atmosfery? Powietrze ulega przebiciu (jonizacji) w polu elektrycznym 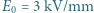 .
.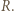 Rozkład ładunku na nim będzie taki sam, jak na powierzchni przewodzącej kuli naładowanej do potencjału
Rozkład ładunku na nim będzie taki sam, jak na powierzchni przewodzącej kuli naładowanej do potencjału 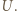 Niech ładunek tej kuli wynosi
Niech ładunek tej kuli wynosi 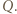 Mamy:
Mamy: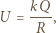
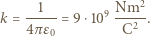
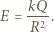
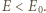 Otrzymujemy więc:
Otrzymujemy więc: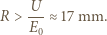
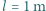 płynie prąd
płynie prąd 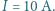 Ile wynosi pęd przenoszony przez elektrony? Masa elektronu
Ile wynosi pęd przenoszony przez elektrony? Masa elektronu 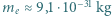 , a jego ładunek
, a jego ładunek 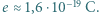
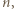 to prąd
to prąd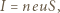
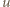 oznacza średnią prędkość ruchu elektronów w kierunku zgodnym z przyłożonym polem elektrycznym, a
oznacza średnią prędkość ruchu elektronów w kierunku zgodnym z przyłożonym polem elektrycznym, a 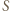 jest polem przekroju przewodnika. W odcinku przewodnika o długości
jest polem przekroju przewodnika. W odcinku przewodnika o długości 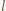 wypadkowy pęd
wypadkowy pęd 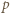 elektronów związany z tym ruchem wynosi:
elektronów związany z tym ruchem wynosi: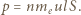
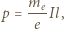
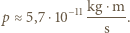
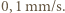

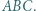 Kąt
Kąt 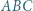 jest równy
jest równy 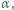 bok
bok 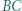 ma długość
ma długość 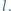 Z jakimi przyspieszeniami zaczną poruszać się kulki po przecięciu nici
Z jakimi przyspieszeniami zaczną poruszać się kulki po przecięciu nici 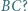 Masa kulki jest równa
Masa kulki jest równa 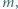 ładunek każdej z nich wynosi
ładunek każdej z nich wynosi 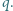 Sił ciężkości nie uwzględniamy.
Sił ciężkości nie uwzględniamy.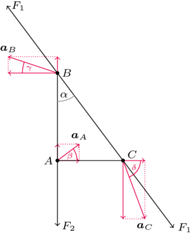
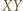 jak na rysunku obok. Ponieważ kulki
jak na rysunku obok. Ponieważ kulki 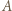 i
i 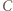 połączone są nicią, mają wzdłuż osi
połączone są nicią, mają wzdłuż osi 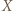 jednakowe przyspieszenia. Na układ tych kulek działają siły
jednakowe przyspieszenia. Na układ tych kulek działają siły 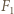 i
i 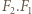 jest siłą oddziaływania elektrycznego między kulkami
jest siłą oddziaływania elektrycznego między kulkami 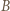 i
i 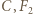 jest wypadkową siły Coulomba między kulkami
jest wypadkową siły Coulomba między kulkami 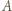 i
i 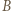 oraz siły naprężenia nici
oraz siły naprężenia nici 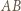 i nie ma składowej wzdłuż osi
i nie ma składowej wzdłuż osi 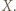 Równanie ruchu układu wzdłuż osi
Równanie ruchu układu wzdłuż osi 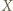 ma postać:
ma postać: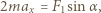
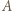 i
i 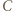 na oś
na oś 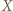 są równe
są równe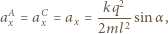
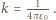 Analogicznie dla układu kulek
Analogicznie dla układu kulek 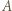 i
i 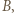 również połączonych nicią,
również połączonych nicią,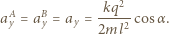
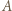 jest równa:
jest równa: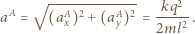
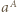 tworzy z osią
tworzy z osią 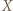 kąt
kąt 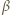 taki, że
taki, że 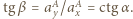 Równanie ruchu kulki
Równanie ruchu kulki 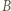 w kierunku osi
w kierunku osi 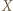 ma postać
ma postać 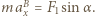 Stąd:
Stąd: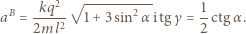
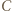 otrzymujemy:
otrzymujemy: 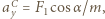

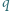 i masie
i masie 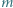 wpada w obszar jednorodnego pola magnetycznego. Prędkość cząstki tworzy różny od zera kąt z wektorem indukcji
wpada w obszar jednorodnego pola magnetycznego. Prędkość cząstki tworzy różny od zera kąt z wektorem indukcji 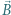 pola. Ile wynosi częstotliwość
pola. Ile wynosi częstotliwość 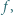 z jaką cząstka obiega kierunek pola
z jaką cząstka obiega kierunek pola 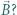
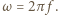 Siłą dośrodkową jest tu siła Lorentza. Mamy więc:
Siłą dośrodkową jest tu siła Lorentza. Mamy więc: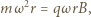
 jest promieniem okręgu,
jest promieniem okręgu, 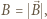 a
a 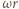 jest wartością składowej prędkości prostopadłej do wektora indukcji
jest wartością składowej prędkości prostopadłej do wektora indukcji 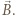 Otrzymujemy więc
Otrzymujemy więc 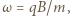 czyli:
czyli: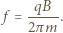
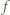 nie zależy od kierunku i wartości prędkości cząstki. Fakt ten wykorzystywany jest do wyznaczania efektywnych mas nośników prądu (elektronów i dziur) w półprzewodnikach.
nie zależy od kierunku i wartości prędkości cząstki. Fakt ten wykorzystywany jest do wyznaczania efektywnych mas nośników prądu (elektronów i dziur) w półprzewodnikach.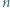 identycznych baterii o sile elektromotorycznej
identycznych baterii o sile elektromotorycznej 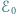 i oporze wewnętrznym
i oporze wewnętrznym 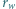 każda. Chcemy uzyskać jak największą moc wydzieloną na oporniku podłączonym do źródła zbudowanego z tych baterii. Jaką moc możemy uzyskać, łącząc baterie (a) szeregowo i (b) równolegle? Ile powinien wynosić opór
każda. Chcemy uzyskać jak największą moc wydzieloną na oporniku podłączonym do źródła zbudowanego z tych baterii. Jaką moc możemy uzyskać, łącząc baterie (a) szeregowo i (b) równolegle? Ile powinien wynosić opór 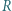 dołączanego opornika w każdym z przypadków, by wydzielona moc była maksymalna?
dołączanego opornika w każdym z przypadków, by wydzielona moc była maksymalna?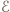 i oporze wewnętrznym
i oporze wewnętrznym 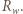 W przypadku (a)
W przypadku (a) 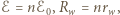 a w przypadku (b)
a w przypadku (b) 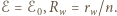 Moc
Moc 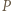 wydzielana na oporze
wydzielana na oporze 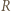 dołączonym do źródła o danych
dołączonym do źródła o danych 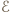 i
i 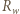 wynosi:
wynosi: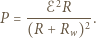
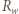 moc
moc 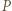 osiąga maksimum dla
osiąga maksimum dla 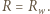 W przypadku (a) należy więc do układu baterii podłączyć opór
W przypadku (a) należy więc do układu baterii podłączyć opór 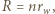 a w przypadku (b)
a w przypadku (b) 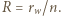 Jak łatwo sprawdzić, moc wydzielana na optymalnie dobranym oporze
Jak łatwo sprawdzić, moc wydzielana na optymalnie dobranym oporze 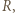 w obu przypadkach wynosi tyle samo:
w obu przypadkach wynosi tyle samo: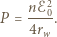
 baterii i moc wydzielana na oporze wewnętrznym każdej z nich są w obu przypadkach takie same.
baterii i moc wydzielana na oporze wewnętrznym każdej z nich są w obu przypadkach takie same.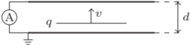
 cienka płytka naładowana równomiernie ładunkiem
cienka płytka naładowana równomiernie ładunkiem 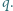 Znaleźć natężenie prądu w obwodzie przedstawionym na rysunku. Odległość między okładkami wynosi
Znaleźć natężenie prądu w obwodzie przedstawionym na rysunku. Odległość między okładkami wynosi 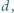 efekty brzegowe można zaniedbać.
efekty brzegowe można zaniedbać.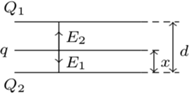
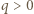 jest nieruchoma i znajduje się w odległości
jest nieruchoma i znajduje się w odległości 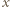 od jednej z okładek. Okładki kondensatora są zwarte drutem i uziemione, zatem napięcie między nimi wynosi zero. Wartości natężeń pola elektrycznego w obszarach zaznaczonych na rysunku wynoszą:
od jednej z okładek. Okładki kondensatora są zwarte drutem i uziemione, zatem napięcie między nimi wynosi zero. Wartości natężeń pola elektrycznego w obszarach zaznaczonych na rysunku wynoszą:
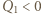 i
i 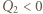 to ładunki na okładkach kondensatora,
to ładunki na okładkach kondensatora, 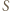 jest powierzchnią płytki. Spełniony jest związek
jest powierzchnią płytki. Spełniony jest związek 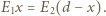 Ponieważ potencjał okładek kondensatora wynosi zero, na zewnątrz kondensatora nie ma pola elektrycznego, stąd
Ponieważ potencjał okładek kondensatora wynosi zero, na zewnątrz kondensatora nie ma pola elektrycznego, stąd 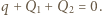 Eliminując z powyższych równań
Eliminując z powyższych równań 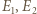 i
i 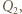 otrzymujemy związek
otrzymujemy związek 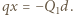 Przesunięcie płytki o
Przesunięcie płytki o 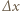 powoduje zmianę ładunku
powoduje zmianę ładunku 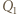 o
o 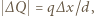 czyli przepływ prądu między okładkami kondensatora o natężeniu
czyli przepływ prądu między okładkami kondensatora o natężeniu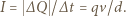
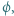 do jakiego może naładować się oddalona od innych ciał kulka miedziana oświetlona światłem o długości fali
do jakiego może naładować się oddalona od innych ciał kulka miedziana oświetlona światłem o długości fali 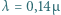 m. Praca wyjścia dla miedzi wynosi
m. Praca wyjścia dla miedzi wynosi 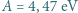 .
.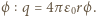 Maksymalny potencjał kulki
Maksymalny potencjał kulki 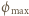 zależy od początkowej energii kinetycznej fotoelektronów. Ponieważ przyrost energii kinetycznej elektronów jest równy pracy sił pola kulki, więc przyjmując, że potencjał pola kulki i prędkość elektronów w nieskończoności wynoszą zero, dostajemy:
zależy od początkowej energii kinetycznej fotoelektronów. Ponieważ przyrost energii kinetycznej elektronów jest równy pracy sił pola kulki, więc przyjmując, że potencjał pola kulki i prędkość elektronów w nieskończoności wynoszą zero, dostajemy: 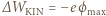 (gdzie
(gdzie  ładunek elektronu). Stąd
ładunek elektronu). Stąd 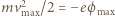 (gdzie
(gdzie 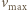 maksymalna energia fotoelektronu) a
maksymalna energia fotoelektronu) a 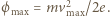 Zgodnie ze wzorem Einsteina dla zjawiska fotoelektrycznego
Zgodnie ze wzorem Einsteina dla zjawiska fotoelektrycznego 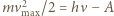 (gdzie
(gdzie  częstość światła). Ostatecznie
częstość światła). Ostatecznie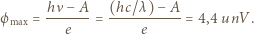
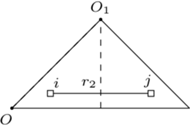
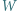 przeciw siłom pola elektrycznego. Jaką pracę trzeba wykonać, żeby ponownie złożyć na pół otrzymany trójkąt?
przeciw siłom pola elektrycznego. Jaką pracę trzeba wykonać, żeby ponownie złożyć na pół otrzymany trójkąt?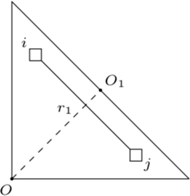
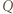 oznacza ładunek płytki,
oznacza ładunek płytki, 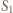 jej powierzchnię,
jej powierzchnię, 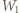 energię płytki, czyli sumę energii oddziaływania ładunków na poszczególnych elementach dielektryka. Na
energię płytki, czyli sumę energii oddziaływania ładunków na poszczególnych elementach dielektryka. Na 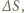 odległe od siebie o
odległe od siebie o 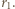 Ładunek każdego elementu wynosi
Ładunek każdego elementu wynosi 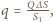 ich energia oddziaływania
ich energia oddziaływania 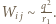 Po złożeniu ładunek płytki pozostaje niezmieniony, jej powierzchnia
Po złożeniu ładunek płytki pozostaje niezmieniony, jej powierzchnia 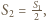 elementy odpowiadające poprzednio rozważanym mają powierzchnię
elementy odpowiadające poprzednio rozważanym mają powierzchnię 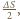 a ich odległość wynosi
a ich odległość wynosi 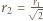 (
(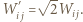 Całkowita energia złożonego dielektryka wynosi
Całkowita energia złożonego dielektryka wynosi 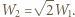 Praca wykonana przy składaniu dana jest wzorem
Praca wykonana przy składaniu dana jest wzorem 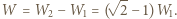 Po kolejnym złożeniu wykonana praca wynosi
Po kolejnym złożeniu wykonana praca wynosi 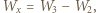 gdzie energia podwójnie złożonego dielektryka
gdzie energia podwójnie złożonego dielektryka 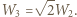 Szukana praca dana jest wzorem:
Szukana praca dana jest wzorem: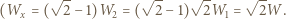

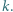 Pole powierzchni każdej okładki wynosi
Pole powierzchni każdej okładki wynosi 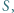 początkowa odległość między nimi
początkowa odległość między nimi 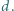 Okładki podłączono do źródła napięcia stałego. Przy jakiej maksymalnej wartości tego napięcia okładki nie zetkną się, jeżeli są stale równoległe względem siebie?
Okładki podłączono do źródła napięcia stałego. Przy jakiej maksymalnej wartości tego napięcia okładki nie zetkną się, jeżeli są stale równoległe względem siebie?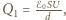 a jego energia wynosi
a jego energia wynosi 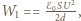 gdzie
gdzie 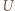 jest napięciem między okładkami a
jest napięciem między okładkami a 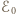 przenikalnością elektryczną próżni. Załóżmy, że ruchoma okładka zatrzyma się, gdy sprężyna zostanie rozciągnięta o
przenikalnością elektryczną próżni. Załóżmy, że ruchoma okładka zatrzyma się, gdy sprężyna zostanie rozciągnięta o 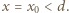 Do chwili zatrzymania ładunek na kondensatorze wzrośnie do wartości
Do chwili zatrzymania ładunek na kondensatorze wzrośnie do wartości 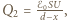 energia osiągnie wartość
energia osiągnie wartość 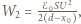 a źródło wykona pracę
a źródło wykona pracę 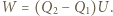 Zasada zachowania energii ma postać
Zasada zachowania energii ma postać 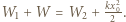 Otrzymujemy stąd równanie
Otrzymujemy stąd równanie 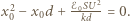 Ma ono rozwiązanie, gdy
Ma ono rozwiązanie, gdy 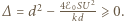 Stąd szukana maksymalna wartość napięcia
Stąd szukana maksymalna wartość napięcia 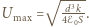 Odpowiadająca jej odległość między okładkami ma wartość
Odpowiadająca jej odległość między okładkami ma wartość 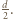
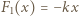 i siła przyciągania elektrostatycznego między okładkami
i siła przyciągania elektrostatycznego między okładkami 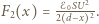 Jeżeli okładka zatrzyma się, gdy
Jeżeli okładka zatrzyma się, gdy 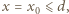 to jej zmiana energii kinetycznej wynosi
to jej zmiana energii kinetycznej wynosi 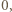 a z drugiej strony równa jest pracy wypadkowej siły działającej na okładkę:
a z drugiej strony równa jest pracy wypadkowej siły działającej na okładkę: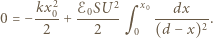
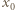 jak w poprzednim rozwiązaniu.
jak w poprzednim rozwiązaniu.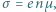 gdzie
gdzie 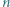 to koncentracja elektronów swobodnych,
to koncentracja elektronów swobodnych,  - ładunek elektronu a
- ładunek elektronu a 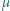 - ruchliwość, będąca współczynnikiem proporcjonalności między zewnętrznym polem elektrycznym i dodatkową prędkością uzyskiwaną przez elektrony, zależnym od rozpraszania elektronów na domieszkach i drganiach sieci krystalicznej.
- ruchliwość, będąca współczynnikiem proporcjonalności między zewnętrznym polem elektrycznym i dodatkową prędkością uzyskiwaną przez elektrony, zależnym od rozpraszania elektronów na domieszkach i drganiach sieci krystalicznej.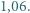 Obliczyć stosunek ruchliwości elektronów w tych metalach, przyjmując, że każdy atom dostarcza jeden elektron przewodnictwa.
Obliczyć stosunek ruchliwości elektronów w tych metalach, przyjmując, że każdy atom dostarcza jeden elektron przewodnictwa.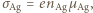 a
a 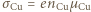 to
to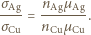
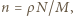 gdzie
gdzie 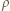 to gęstość,
to gęstość, 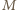 - ciężar atomowy, a
- ciężar atomowy, a 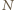 - liczba Avogadro, otrzymujemy:
- liczba Avogadro, otrzymujemy: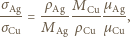
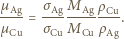
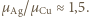
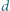 jest równomiernie naładowana ładunkiem
jest równomiernie naładowana ładunkiem 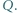 Na osi symetrii płytki prostopadłej do jej płaszczyzny, w odległości
Na osi symetrii płytki prostopadłej do jej płaszczyzny, w odległości 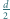 od płytki, umieszczono ładunek punktowy
od płytki, umieszczono ładunek punktowy 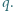 Znaleźć wartość siły elektrostatycznej działającej na ten ładunek.
Znaleźć wartość siły elektrostatycznej działającej na ten ładunek.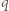 przez powierzchnię tego sześcianu wynosi
przez powierzchnię tego sześcianu wynosi 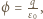 gdzie
gdzie 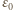 jest przenikalnością elektryczną próżni. Strumień pola przez powierzchnię płytki jest równy
jest przenikalnością elektryczną próżni. Strumień pola przez powierzchnię płytki jest równy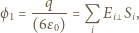
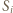 jest elementem powierzchni płytki, a
jest elementem powierzchni płytki, a 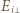 składową wektora natężenia pola elektrycznego prostopadłą do płytki w miejscu, w którym znajduje się i-ty element powierzchni. Gęstość powierzchniowa ładunku płytki wynosi
składową wektora natężenia pola elektrycznego prostopadłą do płytki w miejscu, w którym znajduje się i-ty element powierzchni. Gęstość powierzchniowa ładunku płytki wynosi 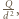 szukana wartość siły działającej na płytkę dana jest wzorem
szukana wartość siły działającej na płytkę dana jest wzorem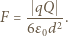
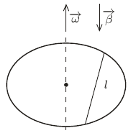
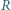 umocowany jest wzdłuż cięciwy drut o długości l. Dysk obraca się ze stałą prędkością kątową
umocowany jest wzdłuż cięciwy drut o długości l. Dysk obraca się ze stałą prędkością kątową 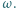 Wektor indukcji jednorodnego pola magnetycznego
Wektor indukcji jednorodnego pola magnetycznego 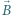 skierowany jest prostopadle do dysku. Znaleźć siłę elektromotoryczną indukcji między środkiem a końcem drutu.
skierowany jest prostopadle do dysku. Znaleźć siłę elektromotoryczną indukcji między środkiem a końcem drutu.
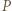 w odległości
w odległości 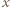 od środka drutu (
od środka drutu (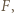 której składowa, równoległa do drutu, dana jest wzorem:
której składowa, równoległa do drutu, dana jest wzorem: 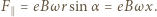 Średnia wartość tej składowej na odcinku o długości
Średnia wartość tej składowej na odcinku o długości 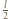 jest równa
jest równa 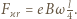 Szukane napięcie wynosi:
Szukane napięcie wynosi: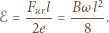
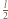 (
(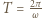 między dwoma współśrodkowymi przewodzącymi okręgami o promieniach
między dwoma współśrodkowymi przewodzącymi okręgami o promieniach 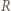 i
i 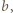 gdzie
gdzie 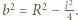 Szybkość zmian strumienia pola magnetycznego w obwodzie przedstawionym na
Szybkość zmian strumienia pola magnetycznego w obwodzie przedstawionym na 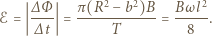
 w jednorodnym polu magnetycznym o indukcji
w jednorodnym polu magnetycznym o indukcji 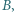 równoległym do powierzchni Ziemi. Płaszczyzna płytki jest równoległa do linii pola magnetycznego i prostopadła do powierzchni Ziemi. Grubość płytki
równoległym do powierzchni Ziemi. Płaszczyzna płytki jest równoległa do linii pola magnetycznego i prostopadła do powierzchni Ziemi. Grubość płytki 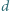 jest dużo mniejsza od jej promienia
jest dużo mniejsza od jej promienia 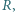 przyspieszenie ziemskie ma wartość
przyspieszenie ziemskie ma wartość 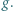
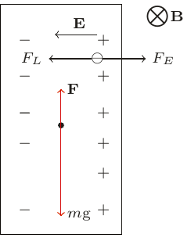
 Na swobodne elektrony w płytce działa w polu magnetycznym siła Lorentza
Na swobodne elektrony w płytce działa w polu magnetycznym siła Lorentza 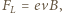 gdzie
gdzie  jest wartością bezwzględną ładunku elektronu. W wyniku tego elektrony przemieszczają się na lewą stronę płytki. Powoduje to powstanie pola elektrycznego
jest wartością bezwzględną ładunku elektronu. W wyniku tego elektrony przemieszczają się na lewą stronę płytki. Powoduje to powstanie pola elektrycznego 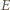 skierowanego jak na rysunku. Elektrony przestają się przemieszczać, gdy siła Lorentza zostaje zrównoważona przez siłę elektryczną
skierowanego jak na rysunku. Elektrony przestają się przemieszczać, gdy siła Lorentza zostaje zrównoważona przez siłę elektryczną 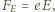 czyli zachodzi związek
czyli zachodzi związek 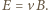 Ponieważ grubość płytki jest dużo mniejsza od jej promienia, możemy ją traktować jako kondensator płaski, w którym napięcie między powierzchniami wynosi
Ponieważ grubość płytki jest dużo mniejsza od jej promienia, możemy ją traktować jako kondensator płaski, w którym napięcie między powierzchniami wynosi 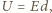 a ładunek na powierzchniach
a ładunek na powierzchniach 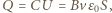 gdzie
gdzie 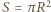 jest powierzchnią płytki. Gdy prędkość płytki rośnie, zmieniają się ładunki na jej powierzchniach, czyli przez płytkę płynie prąd o natężeniu
jest powierzchnią płytki. Gdy prędkość płytki rośnie, zmieniają się ładunki na jej powierzchniach, czyli przez płytkę płynie prąd o natężeniu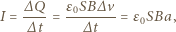
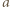 jest przyspieszeniem płytki. Na przewodnik z prądem w polu magnetycznym działa siła elektrodynamiczna, która w naszym przypadku ma zwrot pionowo w górę i wartość
jest przyspieszeniem płytki. Na przewodnik z prądem w polu magnetycznym działa siła elektrodynamiczna, która w naszym przypadku ma zwrot pionowo w górę i wartość 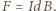 Równanie ruchu płytki ma postać
Równanie ruchu płytki ma postać 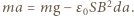 Stąd szukane przyspieszenie jest równe
Stąd szukane przyspieszenie jest równe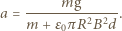
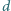 i przenikalności dielektrycznej
i przenikalności dielektrycznej  Na warstwie dielektryka umieszczono kroplę przewodzącej cieczy (elektrolitu) niezwilżającej dielektryka. Jak zmieni się kąt zwilżania
Na warstwie dielektryka umieszczono kroplę przewodzącej cieczy (elektrolitu) niezwilżającej dielektryka. Jak zmieni się kąt zwilżania 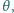 gdy do kropli przyłożymy napięcie
gdy do kropli przyłożymy napięcie 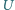 względem metalowej elektrody? Napięcia powierzchniowe wynoszą: ciecz-dielektryk
względem metalowej elektrody? Napięcia powierzchniowe wynoszą: ciecz-dielektryk 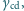 ciecz-gaz otaczający układ
ciecz-gaz otaczający układ 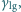 a dielektryk-gaz
a dielektryk-gaz 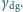
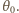 Mamy więc:
Mamy więc: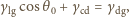
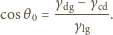
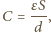 gdzie
gdzie 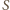 oznacza pole powierzchni styku kropli z dielektrykiem. Energia kondensatora naładowanego do napięcia
oznacza pole powierzchni styku kropli z dielektrykiem. Energia kondensatora naładowanego do napięcia 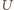 wynosi
wynosi 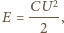 ale trzeba też uwzględnić, że podczas ładowania, źródło napięcia wykonuje pracę potrzebną do pokonania stałego napięcia
ale trzeba też uwzględnić, że podczas ładowania, źródło napięcia wykonuje pracę potrzebną do pokonania stałego napięcia 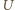 przez przenoszony ładunek
przez przenoszony ładunek 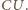 Całkowita zmiana energii układu źródło-kondensator wynosi więc:
Całkowita zmiana energii układu źródło-kondensator wynosi więc: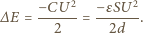
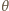 będzie teraz spełniał zależność:
będzie teraz spełniał zależność: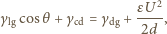
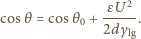
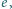 do jego masy
do jego masy 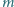 metodą, w której metaliczne próbki poddawali przyspieszeniom. Wyjaśnij, jak to było możliwe. Przyjmij model swobodnych elektronów w metalu.
metodą, w której metaliczne próbki poddawali przyspieszeniom. Wyjaśnij, jak to było możliwe. Przyjmij model swobodnych elektronów w metalu.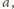 to elektrony przewodnictwa (przyjmujemy, że wewnątrz metalu zachowują się jak cząstki swobodne) doznają względem sieci krystalicznej metalu przyspieszenia
to elektrony przewodnictwa (przyjmujemy, że wewnątrz metalu zachowują się jak cząstki swobodne) doznają względem sieci krystalicznej metalu przyspieszenia 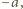 co odpowiada ruchowi w polu elektrycznym
co odpowiada ruchowi w polu elektrycznym 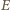 :
: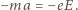
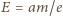 wywołuje przepływ prądu o gęstości
wywołuje przepływ prądu o gęstości 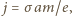 gdzie
gdzie 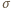 oznacza przewodnictwo właściwe metalu. Wartość tego prądu można zmierzyć i (zmierzywszy również przyspieszenie i przewodnictwo właściwe) wyznaczyć żądany stosunek:
oznacza przewodnictwo właściwe metalu. Wartość tego prądu można zmierzyć i (zmierzywszy również przyspieszenie i przewodnictwo właściwe) wyznaczyć żądany stosunek: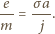
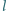 od siebie i puszczono swobodnie. Po czasie
od siebie i puszczono swobodnie. Po czasie 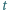 odległość między nimi wzrosła dwukrotnie. Po jakim czasie wzrośnie dwukrotnie odległość między tymi kulkami, gdy ich odległość początkowa będzie wynosić
odległość między nimi wzrosła dwukrotnie. Po jakim czasie wzrośnie dwukrotnie odległość między tymi kulkami, gdy ich odległość początkowa będzie wynosić 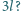
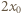 i obliczmy ich prędkości
i obliczmy ich prędkości 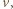 gdy odległość ta osiągnie wartość
gdy odległość ta osiągnie wartość 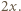 Z zasady zachowania energii otrzymujemy
Z zasady zachowania energii otrzymujemy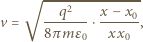
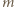 jest masą, a
jest masą, a 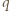 ładunkiem kulki.
ładunkiem kulki.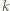 oraz położenia początkowego
oraz położenia początkowego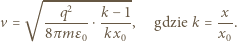
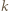 zmienia się od 1 do 2. Podzielmy przemieszczenia kulek w obu rozważanych przypadkach na jednakową liczbę odcinków, dla których
zmienia się od 1 do 2. Podzielmy przemieszczenia kulek w obu rozważanych przypadkach na jednakową liczbę odcinków, dla których 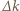 są takie same. Przemieszczenie kulki przy zmianie
są takie same. Przemieszczenie kulki przy zmianie 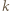 o
o 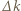 wynosi
wynosi 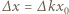 i w drugim przypadku jest 3 razy większe niż w pierwszym:
i w drugim przypadku jest 3 razy większe niż w pierwszym: 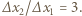 Z
Z 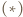 wynika, że dla danego
wynika, że dla danego 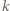 prędkość kulki w pierwszym przypadku jest
prędkość kulki w pierwszym przypadku jest 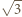 razy większa niż w drugim. Przy zmianie
razy większa niż w drugim. Przy zmianie 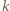 o małe
o małe 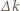 średnie prędkości kulek również będą różnić się
średnie prędkości kulek również będą różnić się 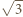 razy:
razy: 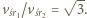 Czasy, w których kulki przemieszczają się o
Czasy, w których kulki przemieszczają się o 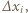 są równe:
są równe: 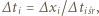 gdzie
gdzie 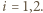 Stosunek tych czasów w rozważanych przypadkach dany jest wzorem
Stosunek tych czasów w rozważanych przypadkach dany jest wzorem 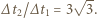 Całkowity czas ruchu w drugim przypadku wynosi
Całkowity czas ruchu w drugim przypadku wynosi 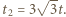
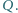 Pierścień spoczywa na poziomej, gładkiej powierzchni, a cały układ znajduje się wewnątrz bardzo długiej cewki prostopadłej do płaszczyzny pierścienia. Ile wyniesie końcowa prędkość kątowa
Pierścień spoczywa na poziomej, gładkiej powierzchni, a cały układ znajduje się wewnątrz bardzo długiej cewki prostopadłej do płaszczyzny pierścienia. Ile wyniesie końcowa prędkość kątowa 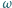 pierścienia, gdy wewnątrz cewki indukcja pola magnetycznego wzrośnie od zera do wartości
pierścienia, gdy wewnątrz cewki indukcja pola magnetycznego wzrośnie od zera do wartości 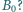
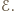 Zgodnie z prawem indukcji Faradaya mamy
Zgodnie z prawem indukcji Faradaya mamy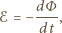
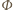 oznacza strumień indukcji przez powierzchnię cewki. Oznacza to, że w każdym punkcie pierścienia, stycznie do niego, na ładunki działa pole elektryczne o wartości
oznacza strumień indukcji przez powierzchnię cewki. Oznacza to, że w każdym punkcie pierścienia, stycznie do niego, na ładunki działa pole elektryczne o wartości 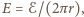 gdzie
gdzie  jest promieniem pierścienia. Liniowa gęstość ładunku na pierścieniu wynosi
jest promieniem pierścienia. Liniowa gęstość ładunku na pierścieniu wynosi 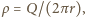 a więc na odcinek
a więc na odcinek 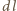 pierścienia działa siła
pierścienia działa siła 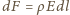 i moment siły względem jego środka to
i moment siły względem jego środka to 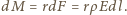 Całkowity moment siły "obracający" pierścień wynosi
Całkowity moment siły "obracający" pierścień wynosi 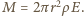 Ten moment siły nadaje pierścieniowi przyspieszenie kątowe
Ten moment siły nadaje pierścieniowi przyspieszenie kątowe 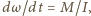 gdzie
gdzie 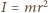 jest momentem bezwładności pierścienia. Otrzymujemy więc
jest momentem bezwładności pierścienia. Otrzymujemy więc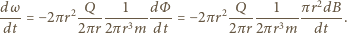
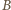 przez pole koła. Po uproszczeniu powtarzających się czynników dostajemy:
przez pole koła. Po uproszczeniu powtarzających się czynników dostajemy: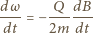
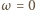 oraz
oraz 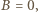 ostatecznie otrzymujemy
ostatecznie otrzymujemy 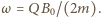
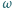 wokół swojej osi. Walec umieszczony jest w jednorodnym polu magnetycznym, którego wektor indukcji
wokół swojej osi. Walec umieszczony jest w jednorodnym polu magnetycznym, którego wektor indukcji  jest równoległy do osi walca. Znaleźć gęstość ładunku wewnątrz walca.
jest równoległy do osi walca. Znaleźć gęstość ładunku wewnątrz walca.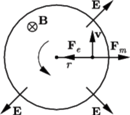
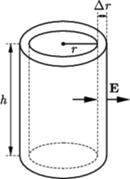
 oraz prędkości kątowej walca
oraz prędkości kątowej walca 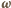 mają zwroty przeciwne (
mają zwroty przeciwne (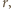 działa siła magnetyczna
działa siła magnetyczna 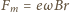 zwrócona na zewnątrz okręgu (
zwrócona na zewnątrz okręgu (  oznacza wartość bezwzględną ładunku elektronu). Wypadkowa siła działająca na elektron jest siłą dośrodkową, zatem siła elektryczna
oznacza wartość bezwzględną ładunku elektronu). Wypadkowa siła działająca na elektron jest siłą dośrodkową, zatem siła elektryczna 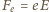 jest większa od siły magnetycznej i ma zwrot do środka okręgu (
jest większa od siły magnetycznej i ma zwrot do środka okręgu ( 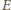 jest natężeniem pola elektrycznego wewnątrz walca). Równanie ruchu elektronu ma postać
jest natężeniem pola elektrycznego wewnątrz walca). Równanie ruchu elektronu ma postać 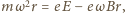 stąd natężenie pola elektrycznego
stąd natężenie pola elektrycznego 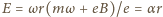 ma zwrot na zewnątrz walca, a jego wartość rośnie liniowo z odległością od środka walca. Rozważmy cienką warstwę cylindryczną o grubości
ma zwrot na zewnątrz walca, a jego wartość rośnie liniowo z odległością od środka walca. Rozważmy cienką warstwę cylindryczną o grubości 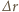 wewnątrz walca (
wewnątrz walca (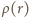 gęstość ładunku wewnątrz tej warstwy, możemy zapisać prawo Gaussa
gęstość ładunku wewnątrz tej warstwy, możemy zapisać prawo Gaussa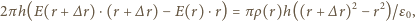
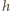 jest wysokością walca. Stąd
jest wysokością walca. Stąd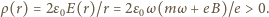
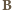 i
i 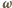 mają zwroty przeciwne, siła magnetyczna działająca na swobodny elektron ma zwrot do środka okręgu, równanie ruchu elektronu ma postać
mają zwroty przeciwne, siła magnetyczna działająca na swobodny elektron ma zwrot do środka okręgu, równanie ruchu elektronu ma postać 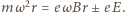 Znak
Znak 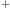 opisuje przypadek, gdy
opisuje przypadek, gdy 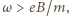 znak
znak  , gdy nierówność ma znak przeciwny. Szukana gęstość ładunku dana jest wzorem
, gdy nierówność ma znak przeciwny. Szukana gęstość ładunku dana jest wzorem 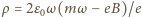 i może być dodatnia albo ujemna. Gdy
i może być dodatnia albo ujemna. Gdy 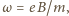 gęstość ładunku wynosi 0.
gęstość ładunku wynosi 0.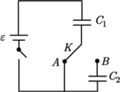
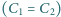 i klucza
i klucza 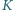 łączymy ze źródłem napięcia o sile elektromotorycznej
łączymy ze źródłem napięcia o sile elektromotorycznej  Wielokrotnie zmieniamy położenie klucza
Wielokrotnie zmieniamy położenie klucza 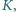 łącząc kondensator
łącząc kondensator 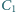 kolejno ze stykami
kolejno ze stykami 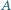 i
i 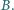 Jak zmienia się napięcie na kondensatorze
Jak zmienia się napięcie na kondensatorze 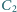 po każdym przełączeniu klucza? Rozważyć przypadki:
po każdym przełączeniu klucza? Rozważyć przypadki: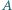 ;
;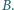
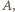 potencjał dolnej okładki kondensatora
potencjał dolnej okładki kondensatora 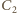 jest taki sam jak potencjał klucza. Napięcie na kondensatorze
jest taki sam jak potencjał klucza. Napięcie na kondensatorze 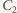 nie zmienia się i wynosi 0.
nie zmienia się i wynosi 0.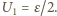 Po przełączeniu klucza do punktu
Po przełączeniu klucza do punktu 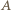 kondensator
kondensator  ładuje się do napięcia
ładuje się do napięcia 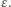 Po ponownym przełączeniu do punktu
Po ponownym przełączeniu do punktu 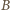 przez źródło przepływa ładunek, napięcie na obu kondensatorach maleje o tę samą wartość
przez źródło przepływa ładunek, napięcie na obu kondensatorach maleje o tę samą wartość 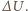 Zgodnie z prawem Kirchhoffa
Zgodnie z prawem Kirchhoffa 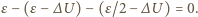 Stąd
Stąd 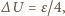 napięcie na drugim kondensatorze wynosi
napięcie na drugim kondensatorze wynosi 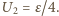 Rozumując analogicznie, otrzymujemy, że po drugim powrocie klucza do położenia
Rozumując analogicznie, otrzymujemy, że po drugim powrocie klucza do położenia 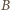 napięcie na kondensatorze
napięcie na kondensatorze 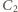 wynosi
wynosi 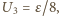 a po
a po 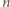 -tym powrocie
-tym powrocie 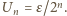 Po odpowiednio długim czasie dolny kondensator rozładuje się.
Po odpowiednio długim czasie dolny kondensator rozładuje się.