Skrót regulaminu

Każdy może nadsyłać rozwiązania zadań z numeru w terminie do końca miesiąca 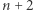. Szkice rozwiązań zamieszczamy w numerze 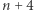. Można nadsyłać rozwiązania czterech, trzech, dwóch lub jednego zadania, można to robić co miesiąc lub z dowolnymi przerwami. Rozwiązanie każdego zadania powinno być pisane na oddzielnym arkuszu papieru oraz podpisane imieniem i nazwiskiem. Uczniowie proszeni są o podanie klasy, studenci -roku i uczelni. Rozwiązania zadań z matematyki i z fizyki należy przysyłać w oddzielnych kopertach, z dopiskiem na kopercie: Klub 44 M lub Klub 44 F. Można także przysyłać je pocztą elektroniczną pod adresem delta@mimuw.edu.pl. Oceniamy zadania w skali od 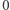do 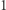z dokładnością do 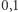. Ocenę mnożymy przez współczynnik trudności danego zadania: 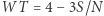, gdzie 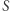oznacza sumę ocen za rozwiązania tego zadania, a 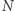- liczbę osób, które nadesłały rozwiązanie choćby jednego zadania z danego numeru w danej konkurencji (M lub F) - i tyle punktów otrzymuje nadsyłający. Po zgromadzeniu 44 punktów, w dowolnym czasie i w którejkolwiek z dwóch konkurencji (M lub F), zostaje on członkiem Klubu 44, a nadwyżka punktów jest zaliczana do ponownego udziału. Trzykrotne członkostwo - to tytuł Weterana.
Szczegółowy regulamin

---

Termin nadsyłania rozwiązań: 30 IV 2019

Rozwiązania zadań z fizyki z numeru 10/2018

* * *

Po raz pierwszy, odkąd redaguję Klub 44F, zdarzyło się, że zadanie osiągnęło współczynnik trudności WT= 4. Mowa o zadaniu 661 z czerwcowego numeru, gdzie należało odpowiedzieć na pytanie, po jakim czasie nić nawinięta na walec - po nadaniu prędkości prostopadłej do nici ciężarkowi na jej końcu - ponownie nawinie się na walec. Może wpływ na to miały letnie upały, chociaż drugie zadanie z czerwca na temat aberracji sferycznej soczewki miało z kolei najniższy współczynnik trudności WT = 1,6. Część uczestników tej serii ograniczyła się do rozwiązania tylko jednego zadania, inni nadesłali rozwiązania niepoprawne. W szczególności nietrafny był pomysł, że kulka porusza się po spirali Archimedesa, która jest złożeniem ruchu po prostej i obrotu po okręgu o nieruchomym środku. W naszym zadaniu środek okręgu przemieszczał się wzdłuż obwodu walca. Należało również uwzględnić fakt, że po całkowitym odwinięciu nici kulka zatacza półokrąg o promieniu równym długości nici i dopiero wtedy zaczyna nawijać się na walec.

Wydaje się, że uczestnicy klubu coraz więcej energii poświęcają na próby znalezienia rozwiązań w różnych źródłach, co chyba nie jest korzystną tendencją, bo to przecież ma być zabawa.

W zadaniu 659 (WT=3,1) pytaliśmy o siłę, z jaką kwadratowa jednorodnie naładowana cienka płytka działa na punktowy ładunek. Ładunek umieszczony został nad środkiem płytki w odległości równej połowie krawędzi płytki, czyli w środku sześcianu, którego jedną ze ścian była płytka. Pozwalało to łatwo obliczyć strumień pola elektrycznego przez powierzchnię płytki i siłę, jaką ładunek działa na płytkę. Wszystkie nadesłane rozwiązania polegały na sumowaniu wkładów do wypadkowej siły od poszczególnych fragmentów płytki, co wymagało wyszukiwania w tablicach odpowiednich całek, i oczywiście takie znęcanie się nie było moim zamiarem. Poprawny wynik otrzymali Mateusz Kapusta i Tomasz Wietecha. Niektóre rozwiązania polegały na podziale płytki na równoległe cienkie pręty i sumowaniu wkładów. Niestety, pole elektryczne od pręta liczone było z prawa Gaussa, jakby pręt miał nieskończoną długość, podczas gdy odległość ładunku była porównywalna z długością pręta.

Drugie pod względem stopnia trudności okazało się zadanie 647 (WT=3,95), gdzie należało znaleźć gęstość ładunku wewnątrz walca obracającego się ze stałą prędkością kątową w jednorodnym, prostopadłym do walca polu magnetycznym. Trzeba tu było wyznaczyć pole elektryczne w płytce, korzystając z warunku równowagi sił działających na swobodny elektron, a następnie z prawa Gaussa wyznaczyć gęstość ładunku.

Trudne okazało się również zadanie 650 (WT=3,74), gdzie żadne z proponowanych rozwiązań nie uzyskało oceny wyższej niż 0,2. Polegało ono na znalezieniu czasu, po którym jeden relatywistyczny pojazd dogoni drugi, z punktu widzenia kosmonauty znajdującego się w jednym z pojazdów. W rozwiązaniu przedstawionym w majowej Delcie błędnie zapisany został niestety wzór na relatywistyczną prędkość względną - z pierwiastkiem w mianowniku!

Pozostałe zadania zostały rozwiązane bezbłędnie przez co najmniej jedną osobę. Za zadanie 652 (WT=2,8) - przyspieszenie metalowej okrągłej płytki spadającej w równoległym do powierzchni Ziemi polu magnetycznym) maksymalną ocenę otrzymał Dawid Zapolski, za zadanie 653 (WT=2,86) - parcie na dno w obracającym się naczyniu z wodą) Tomasz Wietecha. Pan Tomasz rozwiązał bezbłędnie czternaście zadań, Jan Zambrzycki siedem, Mateusz Kapusta, który niedawno rozpoczął przysyłać swoje rozwiązania, trzy.

Wszystkim, którzy przysłali w tym roku rozwiązania zadań, serdecznie dziękuję.