Deltoid
w - k + s = 2
Oznaczmy przez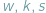 
liczby odpowiednio wierzchołków, krawędzi i ścian wielościanu. W każdym wierzchołku schodzą się co najmniej trzy końce krawędzi i każda krawędź ma dwa końce, zatem 
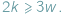Podobnie każda ściana ma co najmniej trzy boki, a każda krawędź należy do dwóch ścian, więc 
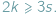Ponadto jeśli wielościan jest wypukły, zachodzi wzór Eulera: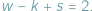 
Wzór ten zachodzi również dla spójnych grafów planarnych (więcej o tym w Deltoidzie 8/2011). Na stronie http://www.ics.uci.edu/ eppstein/junkyard/euler spisano 20 jego dowodów.
Można wykazać, że jeśli dodatnie liczby całkowite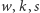 
spełniają powyższe trzy warunki oraz 
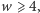to istnieje wielościan wypukły o 
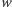wierzchołkach, 
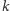krawędziach i 
ścianach. Dowód tego i podobnych faktów opisano w Delcie 8/2015.