Kącik przestrzenny
Sfery Dandelina
Sfery, o których jest mowa na sąsiedniej stronie, nazywane są sferami Dandelina na cześć francuskiego matematyka Germinala Pierra Dandelina (1794–1847), który badając stożkowe, rozwinął pomysły Apoloniusza z Pergi (III w. p.n.e.).
Związane z nimi zależności pozwalają błyskawicznie rozwiązać wiele zadań dotyczących stożkowych. Tu zajmiemy się tylko elipsami. Zaczniemy od zadania, które rozwiązaliśmy w Kąciku 2 inną metodą.
Zachęcam Czytelnika do porównania tego rozumowania z rozwiązaniem tego zadania przedstawionym w Kąciku 2. Okazuje się, że spora część tego rozwiązania jest właściwie ukryta w powyższym. Opisana tu metoda to spojrzenie z nieco innego punktu widzenia, co czasem pozwala na wymyślenie krótszego rozwiązania.
Spójrzmy na inne zadanie, które także można bardzo szybko rozwiązać, wykorzystując sfery Dandelina.
Jeśli Czytelnik nie zna tej własności, o której mowa, to łatwo ją udowodni, wykorzystując poniższy fakt (dowód można też znaleźć np. w broszurze 51. Olimpiady Matematycznej).
Fakt.
Dana jest elipsa o ogniskach
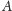 i
i
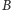 i punkt
i punkt
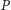 leżący
na zewnątrz elipsy. Proste
leżący
na zewnątrz elipsy. Proste
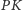 i
i
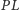 są styczne do tej elipsy.
Wówczas
są styczne do tej elipsy.
Wówczas